2023-2024学年新疆生产建设兵团第三师图木舒克市第一中学高二上学期分班考试数学试题含答案

这是一份2023-2024学年新疆生产建设兵团第三师图木舒克市第一中学高二上学期分班考试数学试题含答案，共17页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。
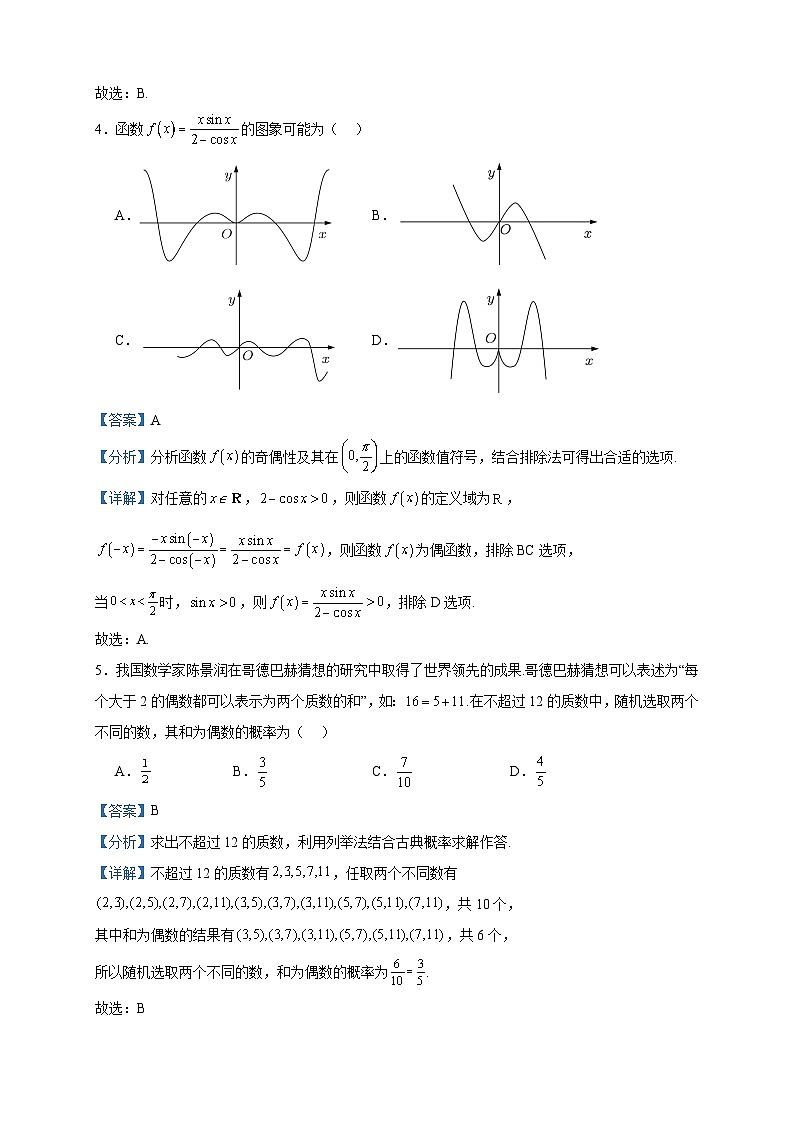
2023-2024学年新疆生产建设兵团第三师图木舒克市第一中学高二上学期分班考试数学试题 一、单选题1．设集合，，则（    ）A． B．C． D．【答案】A【分析】根据集合的交集，可得答案.【详解】由题意，.故选：A.2．已知复数满足，为虚数单位，则（    ）A． B． C． D．【答案】B【分析】由复数的乘法运算，先化简复数，再结合共轭复数的定义可得出答案.【详解】由，可得所以故选：B3．设，则的大小关系为（    ）A． B．C． D．【答案】B【分析】根据指数函数、对数函数的性质比较大小.【详解】因为，所以，又因为，所以.所以.故选：B.4．函数的图象可能为（    ）A． B．C． D．【答案】A【分析】分析函数的奇偶性及其在上的函数值符号，结合排除法可得出合适的选项.【详解】对任意的，，则函数的定义域为，，则函数为偶函数，排除BC选项，当时，，则，排除D选项.故选：A.5．我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想可以表述为“每个大于2的偶数都可以表示为两个质数的和”，如：.在不超过12的质数中，随机选取两个不同的数，其和为偶数的概率为（    ）A． B． C． D．【答案】B【分析】求出不超过12的质数，利用列举法结合古典概率求解作答.【详解】不超过12的质数有，任取两个不同数有，共10个，其中和为偶数的结果有，共6个，所以随机选取两个不同的数，和为偶数的概率为.故选：B6．已知向量满足，则（    ）A． B． C．0 D．1【答案】B【分析】利用平面向量数量积的运算律，数量积的坐标表示求解作答.【详解】向量满足，所以.故选：B 7．2023年1月底，人工智能研究公司OpenAI发布的名为“ChatGTP”的人工智能聊天程序进入中国，迅速以其极高的智能化水平引起国内关注.深度学习是人工智能的一种具有代表性的实现方法，它是以神经网络为出发点的，在神经网络优化中，指数衰减的学习率模型为，其中L表示每一轮优化时使用的学习率，表示初始学习率，D表示衰减系数，G表示训练迭代轮数，表示衰减速度.已知某个指数衰减的学习率模型的初始学习率为0.8，衰减速度为12，且当训练迭代轮数为12时，学习率衰减为0.5.则学习率衰减到0.2以下（不含0.2）所需的训练迭代轮数至少为（    ）（参考数据：）A．36 B．37 C．38 D．39【答案】A【分析】由已知求得衰减系数，然后根据已知模型列不等式求解．【详解】由已知，得，所以，则有，即，即，即，因此G至少为36.故选：A.8．如图，在棱长为2的正方体中，为的中点，为正方体内部及其表面上的一动点，且，则满足条件的所有点构成的平面图形的周长是（    ）  A． B． C． D．【答案】C【分析】证明出平面，平面，确定过点的截面与正方体各棱的交点，可知截面图形是边长为的正六边形，进而可求得结果.【详解】连接、、、、、、，如下图所示：  因为四边形为正方形，则，平面，平面，，，平面，平面，，同理可得，，平面，同理可证平面，设过点且垂直于的平面为平面，则与平面、平面都平行，平面，平面平面，平面平面，，为的中点，则为的中点，同理可知，平面分别与棱、、、交于中点，易知六边形为正六边形，且其边长为，因此，满足条件的所有点构成的平面图形的周长是.故选：C.【点睛】关键点点睛：本题考查正方体截面周长的计算，解题的关键在于利用正方体的几何性质，找出体对角线的垂面，进而确定截面与垂面平行，并以此作出截面. 二、多选题9．若是任意的非零向量，则下列叙述正确的是（    ）A．若，则 B．若，则C．若，则 D．若，则【答案】CD【分析】由平面向量的有关定义、性质、数量积与向量间的关系逐一判断即可得解．【详解】对于A，若，则向量长度相等，但方向不一定相同，不能得到，故A选项错误；对于B，若，则，即或，故B选项错误；对于C，若，则非零向量方向相同或相反，非零向量方向相同或相反，即的方向相同或相反，故，故C选项正确；对于D，若，则，所以，得，故D选项正确.故选：CD10．如图为国家统计局公布的2017~2022年全国城镇居民人均可支配收入及人均消费支出统计图，则（    ）    A．2017~2022年全国城镇居民人均可支配收入及人均消费支出均呈增长趋势B．2017~2022年全国城镇居民人均消费支出的中位数为27535C．2017~2022年全国城镇居民人均可支配收入的极差大于人均消费支出的极差D．2017~2022年全国城镇居民人均消费支出占人均可支配收入的比例均大于80%【答案】BC【分析】根据图表逐项进行判断即可求解.【详解】对于选项A：由图知2017~2022年全国城镇居民人均可支配收入呈增长趋势，但人均消费支出2020年比2019年少，故A不正确；对于选项B：由图可知2017~2022年全国城镇居民人均消费支出的中位数为，故B正确；对于选项C：2017~2022年全国城镇居民人均可支配收入的极差为，人均消费支出的极差为，因为，所以人均可支配收入的极差大于人均消费支出的极差，故C正确；对于选项D：2022年全国城镇居民人均消费支出占人均可支配收入的比例为，小于80%，故D不正确.故选：BC.11．已知函数 的图象关于直线对称，则（    ）A．B．函数在 上单调递增C．函数的图象关于点成中心对称D．若，则的最小值为【答案】BD【分析】首先利用函数的值求出函数的关系式，进一步利用正弦型函数性质的应用判断A、B、C、D的结论．【详解】解：对于函数的图象关于对称，故，由于，所以，所以，故，所以；对于A：由于，所以，故A错误；对于B：由于，故，故函数在该区间上单调递增，故B正确；对于C：当时，，故C错误；对于D：若，则的最小值为，故D正确．故选：BD．12．下列物体中，能够被整体放入棱长为1（单位：m）的正方体容器（容器壁厚度忽略不计）内的有（    ）A．直径为的球体B．所有棱长均为的四面体C．底面直径为，高为的圆柱体D．底面直径为，高为的圆柱体【答案】ABD【分析】根据题意结合正方体的性质逐项分析判断.【详解】对于选项A：因为，即球体的直径小于正方体的棱长，所以能够被整体放入正方体内，故A正确；对于选项B：因为正方体的面对角线长为，且，所以能够被整体放入正方体内，故B正确；对于选项C：因为正方体的体对角线长为，且，所以不能够被整体放入正方体内，故C不正确；对于选项D：因为，可知底面正方形不能包含圆柱的底面圆，如图，过的中点作，设，可知，则，即，解得，且，即，故以为轴可能对称放置底面直径为圆柱，若底面直径为的圆柱与正方体的上下底面均相切，设圆柱的底面圆心，与正方体的下底面的切点为，可知：，则，即，解得，根据对称性可知圆柱的高为，所以能够被整体放入正方体内，故D正确；故选：ABD.  三、填空题13．已知向量，若，则         ．【答案】【分析】利用向量平行的充分必要条件得到关于的方程，解方程即可求得实数的值.【详解】由题意结合向量平行的充分必要条件可得：，解方程可得：.故答案为：.14．已知函数，则            ．【答案】1【分析】根据给定条件，把代入，利用指数、对数运算计算作答.【详解】函数，所以.故答案为：1 15．已知圆锥的顶点为，为底面圆直径，，，则圆锥的侧面积为         ．【答案】【分析】根据题意求得圆锥的底面半径和母线长，结合圆锥的侧面积公式，即可求解.【详解】如图所示，因为，，所以，圆锥的侧面积为.故答案为：.16．已知，方程有四个不同的根，且满足，则的取值范围为：           .【答案】【分析】根据绝对值的性质、对数函数的单调性化简函数的解析式，并画出函数的图象，利用数形结合思想、函数的对称性、对勾函数的单调性进行求解即可.【详解】因为，所以有，画出函数图象如下图所示：  要想方程有四个不同的根，必有，此时有，且，所以，则有，即，所以，令，对勾函数在上单调递减，所以，即，则，所以.故答案为：.【点睛】方法点睛：有关方程根的问题一般转化为两个函数交点问题，再利用数形结合思想进行求解. 四、解答题17．如图所示，在三棱锥中，，．  (1)求二面角的余弦值；(2)求三棱锥的体积．【答案】(1)(2) 【分析】（1）利用二面角得定义即可求出结果；（2）根据，再利用三棱锥体积公式即可求出结果.【详解】（1）  取的中点，连结，，∵，，∴，，∴为二面角的平面角，在中，，，∴，∴二面角的余弦值为．（2）由（1）得，，，平面，平面，∴平面∵ ，∴.18．已知函数是定义在上的奇函数，且．(1)求函数的解析式，判断在上的单调性并证明；(2)解不等式．【答案】(1)，，增函数；证明见解析(2) 【分析】（1）根据奇函数的定义求得函数解析式，再由单调性的定义证明单调性；（2）利用奇偶性变形不等式，然后由单调性化简后求解．【详解】（1）函数是定义在上的奇函数，，解得：，∴，而，解得，∴，．函数在上为增函数；证明如下：任意，且，则，因为，所以，又因为，，所以，所以，即，所以函数在上为增函数．（2）由题意，不等式可化为，即解不等式，所以，所以，解得所以该不等式的解集为．19．“一切为了每位学生的发展”是新课程改革的核心理念．新高考取消文理分科，采用选科模式，赋予了学生充分的自由选择权．新高考模式下，学生是否选择物理为高考考试科目对大学专业选择有着非常重要的意义．某校为了解高一年级600名学生物理科目的学习情况，将他们某次物理测试成绩（满分100分）按照，，，，，分成6组，制成如图所示的频率分布直方图．(1)求这600名学生中物理测试成绩在内的频数，并且补全这个频率分布直方图；(2)学校建议本次物理测试成绩不低于分的学生选择物理为高考考试科目，若学校希望高一年级恰有65％的学生选择物理为高考考试科目，试求的估计值．（结果精确到0.1）【答案】(1)频数为，作图见解析(2) 【分析】（1）根据频率分布直方图的小矩形面积之和为1求得成绩在内的频率，再求频数，然后根据数据补全的频率分布直方图如图；（2）根据恰有65％的学生选择物理为高考考试科目，先确定a所在区间，再求解.【详解】（1）解：由频率分布直方图可知，成绩在内的频率为:，所以这600名学生中物理成绩在内的频数为，补全的频率分布直方图如图所示：（2）学生物理测试成绩在的频率为，物理测试成绩在的频率为．故要使高一年级恰有65％的学生选择物理为高考考试科目，则，且，解得．20．已知，函数．(1)求图象的对称中心及其单调递增区间；(2)若函数，计算的值．【答案】(1)，Z ，.(Z)(2)2022 【分析】（1）利用向量的数量积运算以及三角恒等变形求得函数解析式，利用正弦函数的性质求得对称中心以及单调递增区间； （2）利用函数的周期性求解可得答案.【详解】（1）由已知得，令Z ，解得，所以图象的对称中心坐标为，，令Z，解得， ，所以单调递增区间为(）；（2），该函数周期为，所以，，，，，因为函数周期为，且，所以，而，所以.21．在中，角A，B，C的对边分别是a，b，c，若(1)求角A的大小；(2)若，求中线AD长的最大值（点D是边BC中点）．【答案】(1)(2) 【分析】(1)利用正弦定理结合两角和得正弦公式即可求出结果；(2)利用余弦定理求出，再利用平面向量关系化简即可求出结果.【详解】（1）因为，由正弦定理可得：,即，,因为，所以，所以，因为,所以.（2）由（1）得，则，所以，即，当且仅当时等号成立，因为点D是边BC中点，所以,两边平方可得：,则，所以，中线AD长的最大值为.22．如图所示，在三棱柱中，是边长为2的正三角形，，在底面上的射影为中点，为的中点．  (1)求证：平面；(2)求直线与所成角的正弦值．【答案】(1)证明见解析；(2). 【分析】（1）取中点，连，利用已知结合线面垂直的性质、判定证明平面，再证得即可作答.（2）由（1）的信息，作出线面角，再借助直角三角形求解作答.【详解】（1）在三棱柱中，取中点，连，依题意，平面，而平面，则，又是正三角形，即有，，平面，于是平面，因为为的中点，则，即四边形是平行四边形，有，则四边形是平行四边形，有，所以平面．（2）由（1）知，，，平面，则平面，而平面，于是平面平面，平面平面，在平面内过作于，则平面，连，因此是直线与平面所成的角，正的边长为2，则，又，，于是，，又，因此，所以直线与平面所成的角的正弦值为．