2023年湖南省各市中考数学试题真题汇编——函数B(含答案)

这是一份2023年湖南省各市中考数学试题真题汇编——函数B(含答案)，共45页。试卷主要包含了所在象限是第 　 　象限等内容，欢迎下载使用。
函数B（真题汇编）2023年湖南省各市中考数学试题全解析版
一．选择题（共8小题）;
1．（2023•邵阳）如图，矩形OABC的顶点B和正方形ADEF的顶点E都在反比例函数y＝（k≠0）的图象上，点B的坐标为（2，4），则点E的坐标为（　　）


A．（4，4） B．（2，2） C．（2，4） D．（4，2）
2．（2023•株洲）如图所示，直线l为二次函数y＝ax2+bx+c（a≠0）的图象的对称轴，则下列说法正确的是（　　）
​

A．b恒大于0 B．a，b同号
C．a．b异号 D．以上说法都不对
3．（2023•怀化）已知压力F（N）、压强P（Pa）与受力面积S（m2）之间有如下关系式：F＝PS．当F为定值时，如图中大致表示压强P与受力面积S之间函数关系的是（　　）
A． B．
C． D．
4．（2023•邵阳）已知P1（x1，y1），P2（x2，y2）是抛物线y＝ax2+4ax+3（a是常数，a≠0）上的点，现有以下四个结论：①该抛物线的对称轴是直线x＝﹣2；②点（0，3）在抛物线上；③若x1＞x2＞﹣2，则y1＞y2；④若y1＝y2，则x1+x2＝﹣2，其中，正确结论的个数为（　　）
A．1个 B．2个 C．3个 D．4个
5．（2023•衡阳）已知m＞n＞0，若关于x的方程x2+2x﹣3﹣m＝0的解为x1，x2（x1＜x2），关于x的方程x2+2x﹣3﹣n＝0的解为x3，x4（x3＜x4）．则下列结论正确的是（　　）
A．x3＜x1＜x2＜x4 B．x1＜x3＜x4＜x2
C．x1＜x2＜x3＜x4 D．x3＜x4＜x1＜x2
6．（2023•永州）已知点M（2，a）在反比例函数的图象上，其中a，k为常数，且k＞0，则点M一定在（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
7．（2023•株洲）下列哪个点在反比例函数的图象上？（　　）
A．P1（1，﹣4） B．P2（4，﹣1） C．P3（2，4） D．
8．（2023•怀化）如图，反比例函数y＝（k＞0）的图象与过点（﹣1，0）的直线AB相交于A、B两点．已知点A的坐标为（1，3），点C为x轴上任意一点．如果S△ABC＝9，那么点C的坐标为（　　）

A．（﹣3，0） B．（5，0）
C．（﹣3，0）或（5，0） D．（3，0）或（﹣5，0）
二．填空题（共4小题）
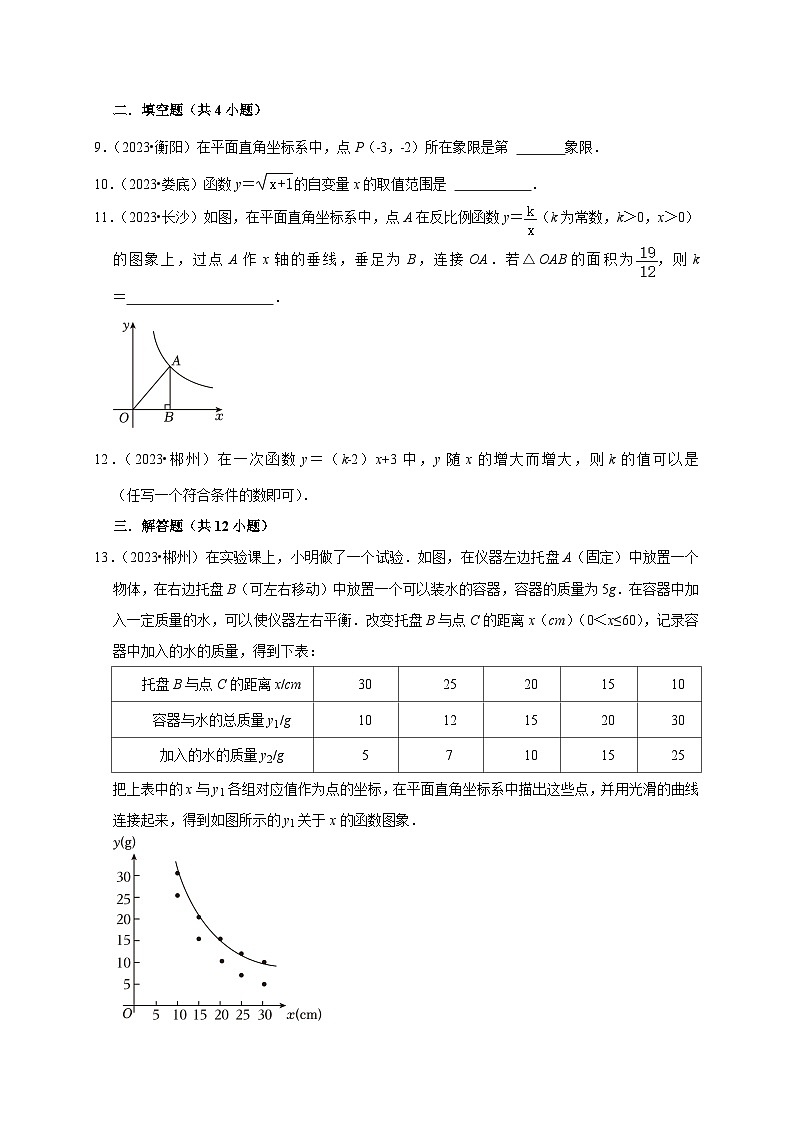
9．（2023•衡阳）在平面直角坐标系中，点P（﹣3，﹣2）所在象限是第 　 　象限．
10．（2023•娄底）函数y＝的自变量x的取值范围是 　 　．
11．（2023•长沙）如图，在平面直角坐标系中，点A在反比例函数y＝（k为常数，k＞0，x＞0）的图象上，过点A作x轴的垂线，垂足为B，连接OA．若△OAB的面积为，则k＝　 　．

12．（2023•郴州）在一次函数y＝（k﹣2）x+3中，y随x的增大而增大，则k的值可以是 　 　（任写一个符合条件的数即可）．
三．解答题（共12小题）
13．（2023•郴州）在实验课上，小明做了一个试验．如图，在仪器左边托盘A（固定）中放置一个物体，在右边托盘B（可左右移动）中放置一个可以装水的容器，容器的质量为5g．在容器中加入一定质量的水，可以使仪器左右平衡．改变托盘B与点C的距离x（cm）（0＜x≤60），记录容器中加入的水的质量，得到下表：
托盘B与点C的距离x/cm
30
25
20
15
10
容器与水的总质量y1/g
10
12
15
20
30
加入的水的质量y2/g
5
7
10
15
25
把上表中的x与y1各组对应值作为点的坐标，在平面直角坐标系中描出这些点，并用光滑的曲线连接起来，得到如图所示的y1关于x的函数图象．

（1）请在该平面直角坐标系中作出y2关于x的函数图象；
（2）观察函数图象，并结合表中的数据：
①猜测y1与x之间的函数关系，并求y1关于x的函数表达式；
②求y2关于x的函数表达式；
③当0＜x≤60时，y1随x的增大而 　 　（填“增大”或“减小”），y2随x的增大而 　 　（填“增大”或“减小”），y2的图象可以由y1的图象向 　 　（以“上”或“下”或“左”或“右”）平移得到．
（3）若在容器中加入的水的质量y2（g）满足19≤y2≤45，求托盘B与点C的距离x（cm）的取值范围．

14．（2023•衡阳）如图，正比例函数y＝x的图象与反比例函数y＝（x＞0）的图象相交于点A．
（1）求点A的坐标．
（2）分别以点O、A为圆心，大于OA一半的长为半径作圆弧，两弧相交于点B和点C，作直线BC，交x轴于点D．求线段OD的长．

15．（2023•永州）小明观察到一个水龙头因损坏而不断地向外滴水，为探究其漏水造成的浪费情况，小明用一个带有刻度的量筒放在水龙头下面装水，每隔一分钟记录量筒中的总水量，但由于操作延误，开始计时的时候量筒中已经有少量水，因而得到如表的一组数据：
时间t
（单位：分钟）
1
2
3
4
5
…
总水量y
（单位：毫升）
7
12
17
22
27
…
（1）探究：根据上表中的数据，请判断和y＝kt+b（k，b为常数）哪一个能正确反映总水量y与时间t的函数关系？并求出y关于t的表达式；
（2）应用：
①请你估算小明在第20分钟测量时量筒的总水量是多少毫升？
②一个人一天大约饮用1500毫升水，请你估算这个水龙头一个月（按30天计）的漏水量可供一人饮用多少天．
16．（2023•株洲）如图所示，在平面直角坐标系Oxy中，四边形OABC为正方形，其中点A、C分别在x轴负半轴，y轴负半轴上，点B在第三象限内，点A（t，0），点P（1，2）在函数 的图象上．
（1）求k的值；
（2）连接BP、CP，记△BCP的面积为S，设T＝2S﹣2t2，求T的最大值．

17．（2023•株洲）某花店每天购进16支某种花，然后出售，如果当天售不完，那么剩下的这种花进行作废处理．该花店记录了10天该种花的日需求量（n为正整数，单位：支），统计如下表：
日需求量n
13
14
15
16
17
18
天数
1
1
2
4
1
1
（1）求该花店在这10天中出现该种花作废处理情形的天数；
（2）当n＜16时，日利润y（单位：元）关于n的函数表达式为：y＝10n﹣80；当n≥16时，日利润为80元．
①当n＝14时，问该花店这天的利润为多少元？
②求该花店这10天中日利润为70元的日需求量的频率．
18．（2023•郴州）已知抛物线y＝ax2+bx+4与x轴相交于点A（1，0），B（4，0），与y轴相交于点C．

（1）求抛物线的表达式；
（2）如图1，点P是抛物线的对称轴l上的一个动点，当△PAC的周长最小时，求的值；
（3）如图2，取线段OC的中点D，在抛物线上是否存在点Q，使tan∠QDB＝？若存在，求出点Q的坐标；若不存在，请说明理由．
19．（2023•株洲）已知二次函数y＝ax2+bx+c（a＞0）．
（1）若a＝1，c＝﹣1，且该二次函数的图象过点（2，0），求b的值；
（2）如图所示，在平面直角坐标系Oxy中，该二次函数的图象与x轴交于点A（x1，0），B（x2，0），且x1＜0＜x2，点D在⊙O上且在第二象限内，点E在x轴正半轴上，连接DE，且线段DE交y轴正半轴于点F，．
①求证：．
②当点E在线段OB上，且BE＝1．⊙O的半径长为线段OA的长度的2倍，若4ac＝﹣a2﹣b2，求2a+b的值．

20．（2023•岳阳）已知抛物线Q1：y＝﹣x2+bx+c与x轴交于A（﹣3，0），B两点，交y轴于点C（0，3）．
（1）请求出抛物线Q1的表达式．
（2）如图1，在y轴上有一点D（0，﹣1），点E在抛物线Q1上，点F为坐标平面内一点，是否存在点E，F使得四边形DAEF为正方形？若存在，请求出点E，F的坐标；若不存在，请说明理由．
（3）如图2，将抛物线Q1向右平移2个单位，得到抛物线Q2，抛物线Q2的顶点为K，与x轴正半轴交于点H，抛物线Q1上是否存在点P，使得∠CPK＝∠CHK？若存在，请求出点P的坐标；若不存在，请说明理由．

21．（2023•衡阳）如图，已知抛物线y＝ax2﹣2ax+3与x轴交于点A（﹣1，0）和点B，与y轴交于点C，连接AC，过B、C两点作直线．
（1）求a的值．
（2）将直线BC向下平移m（m＞0）个单位长度，交抛物线于B′、C′两点．在直线B′C′上方的抛物线上是否存在定点D，无论m取何值时，都是点D到直线B′C′的距离最大．若存在，请求出点D的坐标；若不存在，请说明理由．
（3）抛物线上是否存在点P，使∠PBC+∠ACO＝45°，若存在，请求出直线BP的解析式；若不存在，请说明理由．

22．（2023•怀化）如图一所示，在平面直角坐标系中，抛物线y＝ax2+bx﹣8与x轴交于A（﹣4，0）、B（2，0）两点，与y轴交于点C．

（1）求抛物线的函数表达式及顶点坐标；
（2）点P为第三象限内抛物线上一点，作直线AC，连接PA、PC，求△PAC面积的最大值及此时点P的坐标；
（3）设直线l1：y＝kx+k﹣交抛物线于点M、N，求证：无论k为何值，平行于x轴的直线l2：y＝﹣上总存在一点E，使得∠MEN为直角．
23．（2023•永州）如图1，抛物线y＝ax2+bx+c（a，b，c为常数）经过点F（0，5），
顶点坐标为（2，9），点P（x1，y1）为抛物线上的动点，PH⊥x轴于H，且．
（1）求抛物线的表达式；
（2）如图1，直线OP：交BF于点G，求的最大值；
（3）如图2，四边形OBMF为正方形，PA交y轴于点E，BC交FM的延长线于C，且BC⊥BE，PH＝FC，求点P的横坐标．

24．（2023•邵阳）如图，在平面直角坐标系中，抛物线y＝ax2+x+c经过点A（﹣2，0）和点B（4，0），且与直线l：y＝﹣x﹣1交于D、E两点（点D在点E的右侧），点M为直线l上的一动点，设点M的横坐标为t．
（1）求抛物线的解析式．
（2）过点M作x轴的垂线，与抛物线交于点N．若0＜t＜4，求△NED面积的最大值．
（3）抛物线与y轴交于点C，点R为平面直角坐标系上一点，若以B、C、M、R为顶点的四边形是菱形，请求出所有满足条件的点R的坐标．


函数B（真题汇编）2023年湖南省各市中考数学试题全解析版
参考答案与试题解析
一．选择题（共8小题）
1．（2023•邵阳）如图，矩形OABC的顶点B和正方形ADEF的顶点E都在反比例函数y＝（k≠0）的图象上，点B的坐标为（2，4），则点E的坐标为（　　）

A．（4，4） B．（2，2） C．（2，4） D．（4，2）
【答案】D
【解答】解：∵点B的坐标为（2，4）在反比例函数y＝上，
∴4＝．
∴k＝8．
∴反比例函数的解析式为y＝．
∵点E在反比例函数上，
∴可设（a，）．
∴AD＝a﹣2＝ED＝．
∴a1＝4，a2＝﹣2．
∵a＞0，
∴a＝4．
∴E（4，2）．
故选：D．
2．（2023•株洲）如图所示，直线l为二次函数y＝ax2+bx+c（a≠0）的图象的对称轴，则下列说法正确的是（　　）
​

A．b恒大于0 B．a，b同号
C．a．b异号 D．以上说法都不对
【答案】C
【解答】解：∵直线l为二次函数 y＝ax2+bx+c（a≠0）的图象的对称轴，
∴对称轴为直线，
当a＜0时，则b＞0，
当a＞0时，则b＜0，
∴a，b异号，
故选：C．
3．（2023•怀化）已知压力F（N）、压强P（Pa）与受力面积S（m2）之间有如下关系式：F＝PS．当F为定值时，如图中大致表示压强P与受力面积S之间函数关系的是（　　）
A． B．
C． D．
【答案】D
【解答】解：∵压力F（N）、压强P（Pa）与受力面积S（m2）之间有如下关系式：F＝PS．
∴当F为定值时，压强P与受力面积S之间函数关系是反比例函数，
故选：D．
4．（2023•邵阳）已知P1（x1，y1），P2（x2，y2）是抛物线y＝ax2+4ax+3（a是常数，a≠0）上的点，现有以下四个结论：①该抛物线的对称轴是直线x＝﹣2；②点（0，3）在抛物线上；③若x1＞x2＞﹣2，则y1＞y2；④若y1＝y2，则x1+x2＝﹣2，其中，正确结论的个数为（　　）
A．1个 B．2个 C．3个 D．4个
【答案】B
【解答】解：∵抛物线y＝ax2+4ax+3的对称轴为直线x＝﹣＝﹣2，
∴①正确；
当x＝0时，y＝3，则点点（0，3）在抛物线上，
∴②正确；
当a＞0时，x1＞x2＞﹣2，则y1＞y2；
当a＜0时，x1＞x2＞﹣2，则y1＜y2；
∴③错误；
当y1＝y2，则x1+x2＝﹣4，
∴④错误；
故正确的有2个，
故选：B．
5．（2023•衡阳）已知m＞n＞0，若关于x的方程x2+2x﹣3﹣m＝0的解为x1，x2（x1＜x2），关于x的方程x2+2x﹣3﹣n＝0的解为x3，x4（x3＜x4）．则下列结论正确的是（　　）
A．x3＜x1＜x2＜x4 B．x1＜x3＜x4＜x2
C．x1＜x2＜x3＜x4 D．x3＜x4＜x1＜x2
【答案】B
【解答】解：关于x的方程x2+2x﹣3﹣m＝0的解为抛物线y＝x2+2x﹣3与直线y＝m的交点的横坐标，
关于x的方程x2+2x﹣3﹣n＝0的解为抛物线y＝x2+2x﹣3与直线y＝n的交点的横坐标，
如图：

由图可知，x1＜x3＜x4＜x2，
故选：B．
6．（2023•永州）已知点M（2，a）在反比例函数的图象上，其中a，k为常数，且k＞0，则点M一定在（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
【答案】A
【解答】解：∵点M（2，a）在反比例函数的图象上，
∴a＝，
∴k＞0，
∴a＞0，
∴点M一定在第一象限．
故选：A．
方法二：
∵反比例函数中，k＞0，
∴图象的两个分支在一、三象限，
∵点M（2，a）在反比例函数的图象上，
∴点M一定在第一象限．
故选：A．
7．（2023•株洲）下列哪个点在反比例函数的图象上？（　　）
A．P1（1，﹣4） B．P2（4，﹣1） C．P3（2，4） D．
【答案】D
【解答】解：A．∵1×（﹣4）＝﹣4≠4，∴P1（1，﹣4）不在反比例函数的图象上，故选项不符合题意；
B．∵4×（﹣1）＝﹣4≠4，∴P2（4，﹣1）不在反比例函数的图象上，故选项不符合题意；
C．∵2×4＝8≠4，∴P3（2，4）不在反比例函数的图象上，故选项不符合题意；
D．∵，∴在反比例函数的图象上，故选项符合题意．
故选：D．
8．（2023•怀化）如图，反比例函数y＝（k＞0）的图象与过点（﹣1，0）的直线AB相交于A、B两点．已知点A的坐标为（1，3），点C为x轴上任意一点．如果S△ABC＝9，那么点C的坐标为（　　）

A．（﹣3，0） B．（5，0）
C．（﹣3，0）或（5，0） D．（3，0）或（﹣5，0）
【答案】D
【解答】解：把点A（1，3）代入y＝（k＞0）得，3＝，
∴k＝3，
∴反比例函数为y＝，
设直线AB为y＝ax+b，
代入点D（﹣1，0），A（1，3）得，
解得，
∴直线AB为y＝x+，
解，得或，
∴B（﹣2，﹣），
∵S△ABC＝9，
∴S△ACD+S△BCD＝，
∴CD＝4，
∴点C的坐标为（﹣5，0）或（3，0）．
故选：D．

二．填空题（共4小题）
9．（2023•衡阳）在平面直角坐标系中，点P（﹣3，﹣2）所在象限是第 　三　象限．
【答案】三．
【解答】解：点P（﹣3，﹣2）在第三象限，
故答案为：三．
10．（2023•娄底）函数y＝的自变量x的取值范围是 　x≥﹣1　．
【答案】x≥﹣1．
【解答】解：由题意得：x+1≥0，
解得：x≥﹣1，
故答案为：x≥﹣1．
11．（2023•长沙）如图，在平面直角坐标系中，点A在反比例函数y＝（k为常数，k＞0，x＞0）的图象上，过点A作x轴的垂线，垂足为B，连接OA．若△OAB的面积为，则k＝　　．

【答案】．
【解答】解：△AOB的面积为＝，
所以k＝．
故答案为：．
12．（2023•郴州）在一次函数y＝（k﹣2）x+3中，y随x的增大而增大，则k的值可以是 　3（答案不唯一）　（任写一个符合条件的数即可）．
【答案】见试题解答内容
【解答】解：∵在一次函数y＝（k﹣2）x+3的图象中，y随x的增大而增大，
∴k﹣2＞0，
解得：k＞2．
∴k值可以为3．
故答案为：3（答案不唯一）．
三．解答题（共12小题）
13．（2023•郴州）在实验课上，小明做了一个试验．如图，在仪器左边托盘A（固定）中放置一个物体，在右边托盘B（可左右移动）中放置一个可以装水的容器，容器的质量为5g．在容器中加入一定质量的水，可以使仪器左右平衡．改变托盘B与点C的距离x（cm）（0＜x≤60），记录容器中加入的水的质量，得到下表：
托盘B与点C的距离x/cm
30
25
20
15
10
容器与水的总质量y1/g
10
12
15
20
30
加入的水的质量y2/g
5
7
10
15
25
把上表中的x与y1各组对应值作为点的坐标，在平面直角坐标系中描出这些点，并用光滑的曲线连接起来，得到如图所示的y1关于x的函数图象．

（1）请在该平面直角坐标系中作出y2关于x的函数图象；
（2）观察函数图象，并结合表中的数据：
①猜测y1与x之间的函数关系，并求y1关于x的函数表达式；
②求y2关于x的函数表达式；
③当0＜x≤60时，y1随x的增大而 　减小　（填“增大”或“减小”），y2随x的增大而 　减小　（填“增大”或“减小”），y2的图象可以由y1的图象向 　下　（以“上”或“下”或“左”或“右”）平移得到．
（3）若在容器中加入的水的质量y2（g）满足19≤y2≤45，求托盘B与点C的距离x（cm）的取值范围．

【答案】（1）作出y2关于x的函数图象见解答过程；
（2）①y1是x的反比例函数，y1＝；
②y2＝﹣5；
③减小，减小，下；
（3）6≤x≤12.5．
【解答】解：（1）作出y2关于x的函数图象如下：

（2）①观察表格可知，y1是x的反比例函数，
设y1＝，把（30，10）代入得：10＝，
∴k＝300，
∴y1关于x的函数表达式是y1＝；
②∵y1＝y2+5，
∴y2+5＝；
∴y2＝﹣5；
③观察图象可得，当0＜x≤60时，y1随x的增大而减小，y2随x的增大而减小，y2的图象可以由y1的图象向下平移得到；
故答案为：减小，减小，下；
（3）∵y2＝﹣5，19≤y2≤45，
∴19≤﹣5≤45，
∴24≤≤50，
∴6≤x≤12.5．
14．（2023•衡阳）如图，正比例函数y＝x的图象与反比例函数y＝（x＞0）的图象相交于点A．
（1）求点A的坐标．
（2）分别以点O、A为圆心，大于OA一半的长为半径作圆弧，两弧相交于点B和点C，作直线BC，交x轴于点D．求线段OD的长．

【答案】（1）（3，4）；（2）．
【解答】解：（1）解方程组（x＞0），
得，
∴点A的坐标为（3，4）；
（2）设点D的坐标为（x，0）．
由题意可知，BC是OA的垂直平分线，
∴AD＝OD，
∴（x﹣3）2+42＝x2，
∴x＝，
∴D（，0），OD＝．
15．（2023•永州）小明观察到一个水龙头因损坏而不断地向外滴水，为探究其漏水造成的浪费情况，小明用一个带有刻度的量筒放在水龙头下面装水，每隔一分钟记录量筒中的总水量，但由于操作延误，开始计时的时候量筒中已经有少量水，因而得到如表的一组数据：
时间t
（单位：分钟）
1
2
3
4
5
…
总水量y
（单位：毫升）
7
12
17
22
27
…
（1）探究：根据上表中的数据，请判断和y＝kt+b（k，b为常数）哪一个能正确反映总水量y与时间t的函数关系？并求出y关于t的表达式；
（2）应用：
①请你估算小明在第20分钟测量时量筒的总水量是多少毫升？
②一个人一天大约饮用1500毫升水，请你估算这个水龙头一个月（按30天计）的漏水量可供一人饮用多少天．
【答案】（1）y＝5t+2；
（2）①102毫升；②144天．
【解答】解：（1）根据上表中的数据，y＝kt+b（k，b为常数）能正确反映总水量y与时间t的函数关系，
∵当t＝1时，y＝7，当t＝2时，y＝12，
∴，
∴，
∴y＝5t+2；
（2）①当t＝20时，y＝100+2＝102，
即估算小明在第20分钟测量时量筒的总水量是102毫升；
②当t＝24×60＝1440分钟时，y＝5×1440+2＝7202（毫升），
当t＝0时，y＝2，
∴＝144（天），
答：估算这个水龙头一个月（按30天计）的漏水量可供一人饮用144天．
16．（2023•株洲）如图所示，在平面直角坐标系Oxy中，四边形OABC为正方形，其中点A、C分别在x轴负半轴，y轴负半轴上，点B在第三象限内，点A（t，0），点P（1，2）在函数 的图象上．
（1）求k的值；
（2）连接BP、CP，记△BCP的面积为S，设T＝2S﹣2t2，求T的最大值．

【答案】（1）k＝2；
（2）Tmx＝1．
【解答】解：（1）∵点P（1，2）在函数 的图象上，
∴2＝，
∴k＝2，
即k的值为2；
（2）∵点A（t，0）在x轴负半轴上，
∴OA＝﹣t，
∵四边形OABC为正方形，
∴OC＝BC＝OA＝﹣t，BC∥x轴，
∴△BCP的面积为S＝×（﹣t）×（2﹣t）＝t2﹣t，
∴T＝2S﹣2t2＝2（t2﹣t）﹣2t2＝﹣t2﹣2t＝﹣（t+1）2+1，
∵﹣1＜0，
∴抛物线开口向下，
∴当t＝﹣1时，T有最大值，T的最大值是1．
17．（2023•株洲）某花店每天购进16支某种花，然后出售，如果当天售不完，那么剩下的这种花进行作废处理．该花店记录了10天该种花的日需求量（n为正整数，单位：支），统计如下表：
日需求量n
13
14
15
16
17
18
天数
1
1
2
4
1
1
（1）求该花店在这10天中出现该种花作废处理情形的天数；
（2）当n＜16时，日利润y（单位：元）关于n的函数表达式为：y＝10n﹣80；当n≥16时，日利润为80元．
①当n＝14时，问该花店这天的利润为多少元？
②求该花店这10天中日利润为70元的日需求量的频率．
【答案】（1）花店在这10天中出现该种花作废处理情形的天数为4天；
（2）①当n＝14时，该花店这天的利润为60元；
②该花店这10天中日利润为70元的日需求量的频率为．
【解答】解：（1）1+1+2＝4，
答：花店在这10天中出现该种花作废处理情形的天数为4天；
（2）①当n＝14时，y＝10n﹣80＝10×14﹣80＝60，
答：当n＝14时，该花店这天的利润为60元；
②当n＜16时，70＝10n﹣80，解得：n＝15，
当n＝15时，有2天，
∴＝．
答：该花店这10天中日利润为70元的日需求量的频率为．
18．（2023•郴州）已知抛物线y＝ax2+bx+4与x轴相交于点A（1，0），B（4，0），与y轴相交于点C．

（1）求抛物线的表达式；
（2）如图1，点P是抛物线的对称轴l上的一个动点，当△PAC的周长最小时，求的值；
（3）如图2，取线段OC的中点D，在抛物线上是否存在点Q，使tan∠QDB＝？若存在，求出点Q的坐标；若不存在，请说明理由．
【答案】（1）y＝x2﹣5x+4；
（2）；
（3） 或（，2）或Q（3，﹣2）或．
【解答】解：（1）∵抛物线y＝ax2+bx+4与x轴相交于点A（1，0），B（4，0），
，
解得：，
∴抛物线的表达式为y＝x2﹣5x+4；
（2）由（1）知y＝x2﹣5x+4，当x＝0时，y＝4，

∴C（0，4），抛物线的对称轴为直线，
∵△PAC的周长等于PA+PC+AC，AC为定长，
∴当PA+PC的值最小时，△PAC的周长最小，
∵A，B关于抛物线的对称轴对称，
∴PA+PC＝PB+PC≥BC，当P，B，C三点共线时，PA+PC的值最小，为BC的长，此时点P为直线BC与对称轴的交点，
设直线BC的解析式为：y＝mx+n，
则：，
解得：，
∴直线BC的解析式为y＝﹣x+4，
当 时，，
∴，
∵A（1，0），C（0，4），
∴PA＝＝，PC＝＝，
∴；
（2）存在，
∵D为OC的中点，
∴D（0，2），
∴OD＝2，
∵B（4，0），
∴OB＝4，
在Rt△BOD中，，
，
∴∠QDB＝∠OBD；
①当Q点在D点上方时：过点D作DQ∥OB，交抛物线于点Q，则：∠QDB＝∠OBD，此时Q点纵坐标为2，

设Q点横坐标为t，则：t2﹣5t+4＝2，解得：，
∴Q（，2）或（，2）；
②当点Q在D点下方时：设DQ与x轴交于点E，

则：DE＝BE，
设E（p，0），则：DE2＝OE2+OD2＝p2+4，BE2＝（4﹣p）2，
∴p2+4＝（4﹣p）2，
解得：，
∴，
设DE的解析式为：y＝kx+q，
则：，
解得：，
∴，
联立，
解得：或，
∴Q（3，﹣2）或；
综上所述， 或（，2）或Q（3，﹣2）或．
19．（2023•株洲）已知二次函数y＝ax2+bx+c（a＞0）．
（1）若a＝1，c＝﹣1，且该二次函数的图象过点（2，0），求b的值；
（2）如图所示，在平面直角坐标系Oxy中，该二次函数的图象与x轴交于点A（x1，0），B（x2，0），且x1＜0＜x2，点D在⊙O上且在第二象限内，点E在x轴正半轴上，连接DE，且线段DE交y轴正半轴于点F，．
①求证：．
②当点E在线段OB上，且BE＝1．⊙O的半径长为线段OA的长度的2倍，若4ac＝﹣a2﹣b2，求2a+b的值．

【答案】（1）；（2）①见解析；②0．
【解答】（1）解：∵a＝1，c＝﹣1，
∴二次函数解析式为y＝x2+bx﹣1，
∵该二次函数的图象过点（2，0），
∴4+2b﹣1＝0，
解得：b＝﹣；
（2）①证明：∵∠DOF＝∠DEO，∠ODF＝∠EDO，
∴△DOF∽△DEO，
∴，
∴＝，
∵，
∴；
②解∵该二次函数的图象与x轴交于点A（x1，0），B（x2，0），且x1＜0＜x2，
∴OA＝﹣x1，OB＝x2，
∵BE＝1．
∴OE＝x2﹣1，
∵⊙O的半径长为线段OA的长度的2倍，
∴OD＝﹣2x1，
∵，
∴，
∴3x1+x2﹣1＝0，
即x2＝1﹣3x1①，
∵该二次函数的图象与x轴交于点A（x1，0），B（x2，0），
∴x1，x2是方程ax2+bx+c＝0的两个根，
∴，
∵4ac＝﹣a2﹣b2，a≠0，
∴，
即4（x1x2）+1+（x1+x2）2＝0②
①代入②，即，
即，
整理得﹣8（x1）2＝﹣2，
∴，
解得：（正值舍去），
∴，
∴抛物线的对称轴为直线，
∴b＝﹣2a，
∴2a+b＝0．
20．（2023•岳阳）已知抛物线Q1：y＝﹣x2+bx+c与x轴交于A（﹣3，0），B两点，交y轴于点C（0，3）．
（1）请求出抛物线Q1的表达式．
（2）如图1，在y轴上有一点D（0，﹣1），点E在抛物线Q1上，点F为坐标平面内一点，是否存在点E，F使得四边形DAEF为正方形？若存在，请求出点E，F的坐标；若不存在，请说明理由．
（3）如图2，将抛物线Q1向右平移2个单位，得到抛物线Q2，抛物线Q2的顶点为K，与x轴正半轴交于点H，抛物线Q1上是否存在点P，使得∠CPK＝∠CHK？若存在，请求出点P的坐标；若不存在，请说明理由．

【答案】（1）y＝﹣x2﹣2x+3．
（2）存在，E（﹣2，3），F（1，2）．
（3）点P的坐标为（1，0）或（﹣2，3）．
【解答】解：（1）∵抛物线Q1：y＝﹣x2+bx+c经过A（﹣3，0），C（0，3）两点，
∴，
解得：，
∴抛物线Q1的表达式为y＝﹣x2﹣2x+3．
（2）存在点E，F使得四边形DAEF为正方形．
理由：
如图1，过点E作EG⊥x轴于点G，则∠AGE＝90°＝∠AOD，

∵A（﹣3，0），D（0，﹣1），
∴OA＝3，OD＝1，
∵四边形DAEF是正方形，
∴AE＝AD＝DF，∠DAE＝∠ADF＝90°，
∵∠EAG+∠DAO＝90°，∠DAO+∠ADO＝90°，
∴∠EAG＝∠ADO，
∴△EAG≌△ADO（AAS），
∴AG＝OD＝1，EG＝OA＝3，
∴E（﹣2，3），
当x＝﹣2时，y＝﹣x2﹣2x+3＝﹣（﹣2）2﹣2×（﹣2）+3＝3，
∴点E在抛物线上，
过点F作FL⊥y轴于点L，
同理，△DFL≌△ADO（AAS），
∴FL＝OD＝1，DL＝OA＝3，
∴OL＝DL﹣OD＝3﹣1＝2，
F（1，2）．
（3）抛物线Q1上存在点P，使得∠CPK＝∠CHK．
∵y＝﹣x2﹣2x+3＝﹣（x+1）2+4，
∴抛物线Q1的顶点坐标为（﹣1，4），
∵将抛物线Q1向右平移2个单位，得到抛物线Q2，
∴抛物线Q2的解析式为y＝﹣（x+1﹣2）2+4＝﹣（x﹣1）2+4，
∵抛物线Q2的顶点为K，与x轴正半轴交于点H，
∴K（1，4），H（3，0），
过点K作KT⊥y轴于点T，连接BC，如图2，过点C作PS⊥y轴交BK于点S，交抛物线Q1于点P，连接PK，
则T（0，4），

∴KT＝TC＝1，∠KTC＝90°，
∴△CKT是等腰直角三角形，
∴∠KCT＝45°，CK＝KT＝，
∵OH＝OC＝3，∠COH＝90°，
∴△COH是等腰直角三角形，
∴∠HCO＝45°，CH＝OC＝3，
∴∠KCH＝180°﹣∠KCT﹣∠HCO＝90°，
∴tan∠CHK＝＝＝，
∵∠CPK＝∠CHK，
∴tan∠CPK＝tan∠CHK＝，
∵tan∠BCO＝＝，
∴∠BCO＝∠CHK，
∵BK∥OC，
∴∠CBK＝∠BCO，
∴∠CBK＝∠CHK，
即点P与点B重合时，∠CPK＝∠CHK，
∴P1（1，0）；
∵SK＝1，PS＝3，
∴tan∠CPK＝＝，
∴∠CPK＝∠CHK，
∵点P与点C关于直线x＝﹣1对称，
∴P（﹣2，3）；
综上所述，抛物线Q1上存在点P，使得∠CPK＝∠CHK，点P的坐标为（1，0）或（﹣2，3）．
21．（2023•衡阳）如图，已知抛物线y＝ax2﹣2ax+3与x轴交于点A（﹣1，0）和点B，与y轴交于点C，连接AC，过B、C两点作直线．
（1）求a的值．
（2）将直线BC向下平移m（m＞0）个单位长度，交抛物线于B′、C′两点．在直线B′C′上方的抛物线上是否存在定点D，无论m取何值时，都是点D到直线B′C′的距离最大．若存在，请求出点D的坐标；若不存在，请说明理由．
（3）抛物线上是否存在点P，使∠PBC+∠ACO＝45°，若存在，请求出直线BP的解析式；若不存在，请说明理由．

【答案】（1）a＝﹣1．
（2）存在，D（，）．
（3）抛物线上存在点P，使∠PBC+∠ACO＝45°，直线BP的解析式为y＝﹣x+1或y＝﹣3x+9．．
【解答】解：（1）∵抛物线y＝ax2﹣2ax+3与x轴交于点A（﹣1，0），
∴a+2a+3＝0，
∴a＝﹣1．
（2）存在定点D，无论m取何值时，都是点D到直线B′C′的距离最大．
∵y＝﹣x2+2x+3，
当x＝0时，y＝3，
∴C（0，3），
当y＝0时，﹣x2+2x+3＝0，
解得：x1＝﹣1，x2＝3，
∴B（3，0），
设直线BC的解析式为y＝kx+b，则，
解得：，
∴直线BC的解析式为y＝﹣x+3，
∵将直线BC向下平移m（m＞0）个单位长度，交抛物线于B′、C′两点，
∴直线B′C′的解析式为y＝﹣x+3﹣m，
设D（t，﹣t2+2t+3），
过点D作DE∥y轴，交B′C′于点E，作DF⊥B′C′于点F，设直线B′C′交y轴于点G，如图，

∴E（t，﹣t+3﹣m），
∴DE＝﹣t2+2t+3﹣（﹣t+3﹣m）＝﹣t2+3t+m，
∵OB＝OC＝3，∠BOC＝90°，
∴∠BCO＝∠CBO＝45°，
∵B′C′∥BC，
∴∠B′GO＝∠BCO＝45°，
∵DE∥y轴，
∴∠DEF＝∠B′GO＝45°，
∵∠DFE＝90°，
∴△DEF是等腰直角三角形，
∴DF＝DE＝（﹣t2+3t+m）＝﹣（t﹣）2+（+m），
∵﹣＜0，
∴当t＝时，DF取得最大值（+m），此时点D的坐标为（，）．
（3）存在．
当∠PBC在BC的下方时，在y轴正半轴上取点M（0，1），连接BM交抛物线于点P，如图，

∵A（﹣1，0），B（3，0），C（0，3），M（0，1），
∴OB＝OC＝3，OM＝OA＝1，∠BOM＝∠COA＝90°，
∴△BOM≌△COA（SAS），
∴∠MBO＝∠ACO，
∵∠CBO＝45°，
∴∠CBP+∠MBO＝45°，
∴∠CBP+∠ACO＝45°，
设直线BM的解析式为y＝k′x+b′，则，
解得：，
∴直线BM的解析式为y＝﹣x+1，
联立，得，
解得：（舍去），，
∴P（﹣，）；
当∠PBC在BC的上方时，作点M关于直线BC的对称点M′，如图，连接MM′，CM′，直线BM′交抛物线于P，

由对称得：MM′⊥BC，CM′＝CM＝2，∠BCM′＝∠BCM＝45°，
∴∠MCM′＝90°，
∴M′（2，3），
则直线BM′的解析式为y＝﹣3x+9，
联立，得：，
解得：（舍去），，
∴P（2，3）；
综上所述，抛物线上存在点P，使∠PBC+∠ACO＝45°，直线BP的解析式为y＝﹣x+1或y＝﹣3x+9．
22．（2023•怀化）如图一所示，在平面直角坐标系中，抛物线y＝ax2+bx﹣8与x轴交于A（﹣4，0）、B（2，0）两点，与y轴交于点C．

（1）求抛物线的函数表达式及顶点坐标；
（2）点P为第三象限内抛物线上一点，作直线AC，连接PA、PC，求△PAC面积的最大值及此时点P的坐标；
（3）设直线l1：y＝kx+k﹣交抛物线于点M、N，求证：无论k为何值，平行于x轴的直线l2：y＝﹣上总存在一点E，使得∠MEN为直角．
【答案】（1）抛物线的函数表达式为y＝x2+2x﹣8，顶点坐标为（﹣1，﹣9）；
（2）S△PAC的最大值为8，点P（﹣2，﹣8）；
（3）证明见解答．
【解答】（1）解：∵抛物线y＝ax2+bx﹣8与x轴交于A（﹣4，0）、B（2，0）两点，
∴，
解得：，
∴抛物线的函数表达式为y＝x2+2x﹣8，
∵y＝x2+2x﹣8＝（x+1）2﹣9，
∴抛物线的顶点坐标为（﹣1，﹣9）；
（2）解：∵抛物线y＝x2+2x﹣8与y轴交于点C，
∴C（0，﹣8），
设直线AC的解析式为y＝mx+n，则，
解得：，
∴直线AC的解析式为y＝﹣2x﹣8，
设P（t，t2+2t﹣8），
过点P作PF∥y轴，交AC于点F，如图，

则F（t，﹣2t﹣8），
∴PF＝﹣2t﹣8﹣（t2+2t﹣8）＝﹣t2﹣4t，
∴S△PAC＝S△PAF+S△PCF＝PF•（t+4）+PF•（﹣t）＝2PF＝2（﹣t2﹣4t）＝﹣2（t+2）2+8，
∵﹣2＜0，
∴当t＝﹣2时，S△PAC的最大值为8，此时点P（﹣2，﹣8）；
（3）证明：∵直线l1：y＝kx+k﹣交抛物线于点M、N，
∴x2+2x﹣8＝kx+k﹣，
整理得：x2+（2﹣k）x+﹣k＝0，
∴xM+xN＝k﹣2，xMxN＝﹣k，
∵yM＝kxM+k﹣，yN＝kxN+k﹣，
∴yM﹣yN＝k（xM﹣xN），
∴MN2＝（xM﹣xN）2+（yM﹣yN）2＝（1+k2）（xM﹣xN）2＝（1+k2）[（xM+xN）2﹣4xMxN]＝（1+k2）[（k﹣2）2﹣4（﹣k）]＝（1+k2）2，
∵设MN的中点为O′，
∴O′（，k2﹣），
过点O′作O′E⊥直线l2：y＝﹣，垂足为E，如图，

∴E（，﹣），
∴O′E＝k2﹣﹣（﹣）＝（1+k2），
∴O′E＝MN，
∴以MN为直径的⊙O′一定经过点E，
∴∠MEN＝90°，
∴在直线l2：y＝﹣上总存在一点E，使得∠MEN为直角．
23．（2023•永州）如图1，抛物线y＝ax2+bx+c（a，b，c为常数）经过点F（0，5），
顶点坐标为（2，9），点P（x1，y1）为抛物线上的动点，PH⊥x轴于H，且．
（1）求抛物线的表达式；
（2）如图1，直线OP：交BF于点G，求的最大值；
（3）如图2，四边形OBMF为正方形，PA交y轴于点E，BC交FM的延长线于C，且BC⊥BE，PH＝FC，求点P的横坐标．

【答案】（1）抛物线的表达式为y＝﹣x2+4x+5；
（2）的最大值为；
（3）点P的横坐标为．
【解答】解：（1）∵抛物线y＝ax2+bx+c（a，b，c为常数）经过点F（0，5），顶点坐标为（2，9），
∴，
解得，
∴抛物线的表达式为y＝﹣x2+4x+5；
（2）过点G作GT⊥x轴于点T，如图所示，

在y＝﹣x2+4x+5中，令y＝0得0＝﹣x2+4x+5，
解得x＝5或x＝﹣1，
∴A（﹣1，0），B（5，0），
∵F（0，5），
∴BO＝FO＝5，
设直线BF的解析式为：y＝kx+5，
∴y＝5k+5，
解得k＝﹣1，
∴直线BF的解析式为y＝﹣x+5，
由G在直线BF上，设G（m，﹣m+5），
∵G在直线OP上，直线OP为，
∴﹣m+5＝m，
∴，
∴，
由P（x1，y1） 在抛物线 y＝﹣x2+4x+5上，知P（x1，﹣+4x1+5），
∴，
∵S△BPG＝S△BPO﹣S△BOG，
∴＝＝﹣1＝﹣1＝﹣1，
∵＝＝，
∴＝﹣1＝﹣1＝﹣1＝﹣（x1﹣）2+，
∵，，
∴当 时，取最大值，最大值为；
（3）设MF交PH于T，如图：

∵OBFM为正方形，F（0，5），
∴FM＝BM＝OF＝BO＝5，∠MBO＝90°，FC∥OB，
∵PH⊥x，∠MBO＝90°，FC∥OB，
∴MTBH为矩形，
∴TH＝MB＝FM＝5，
∵PH＝FC，
∴PT＝MC，
∵BC⊥BE，
∴∠MBC+∠MBE＝90°，
∵∠MBO＝90°，
∴∠OBE+∠MBE＝90°，
∴∠OBE＝∠MBC，
∴∠CMB＝∠EOB＝90°，
∴△EOB∽△CMB，
∴，
∵OB＝MB，
∴EO＝MC，
∵PH＝FC，
∴PT＝MC，
∴EO＝MC＝PT，
设 EO＝MC＝PT＝a，
∴PH＝PT+TH＝5+a，E（0，a），
∵A（﹣1，0），
设直线AP的解析式为y＝kx+b，
则，
∴，
∴直线AP的解析式为y＝ax+a，
∵PH＝a+5，P在直线AP上，
∴a+5＝ax+a，
∴，即P点横坐标为 ，
∴x1＝，y1＝a+5，
∴a＝，y1＝+5
∴+5＝﹣+4x1+5，
∴﹣4+5＝0，
∴（x1+1）（﹣5x1+5）＝0，
解得x1＝1或x1＝或x1＝，
∵x1≥，
∴x1＝，
∴点P的横坐标为．
方法2：

设P（m，﹣m2+4m+5），
∴OH＝m，PH＝﹣m2+4m+5，
∵＝tan∠EAO＝，
∴＝，
∴EO＝5﹣m，
∵BC⊥BE，
∴∠CBM＝90°﹣∠MBE＝∠EBO，
∵∠CMB＝90°＝∠EOB，BM＝OB，
∴△CMB≌△EOB（ASA），
∴CM＝EO＝5﹣m，
∴CF＝CM+FM＝5﹣m+5＝10﹣m，
∵PH＝CF，
∴﹣m2+4m+5＝10﹣m，
解得m＝或m＝，
∵m≥，
∴m＝，
∴点P的横坐标为．
24．（2023•邵阳）如图，在平面直角坐标系中，抛物线y＝ax2+x+c经过点A（﹣2，0）和点B（4，0），且与直线l：y＝﹣x﹣1交于D、E两点（点D在点E的右侧），点M为直线l上的一动点，设点M的横坐标为t．
（1）求抛物线的解析式．
（2）过点M作x轴的垂线，与抛物线交于点N．若0＜t＜4，求△NED面积的最大值．
（3）抛物线与y轴交于点C，点R为平面直角坐标系上一点，若以B、C、M、R为顶点的四边形是菱形，请求出所有满足条件的点R的坐标．

【答案】（1）抛物线解析式为y＝﹣x2+x+4；
（2）△NED面积的最大值是7；
（3）R的坐标为（，）或（，）或（，）或（，）或（，）．
【解答】解：（1）把A（﹣2，0），B（4，0）代入y＝ax2+x+c 得：
，
解得：，
∴抛物线解析式为y＝﹣x2+x+4；
（2）联立，
解得或，
∴D（2+，﹣3﹣），E（2﹣，﹣3+），
∵点M为直线l上的一动点，横坐标为t，
∴M（t，﹣t﹣1），
∴N（t，﹣t2+t+4），
∴MN＝﹣t2+t+4﹣（﹣t﹣1）＝﹣t2+2t+5，
∴S△NED＝MN•|xD﹣xE|＝×（﹣t2+2t+5）×2＝﹣（t﹣2）2+7，
∵﹣＜0，0＜t＜4，
∴当t＝2时，S△NED取最大值7，
∴△NED面积的最大值是7；
（3）在y＝﹣x2+x+4中，令x＝0得y＝4，
∴C（0，4），
设M（t，﹣t﹣1），R（m，n），
又B（4，0），
①当BC，MR为对角线时，BC，MR的中点重合，且BM＝CM，
∴，
解得，
∴R（，）；
②当BM，CR为对角线时，BM，CR的中点重合，且BC＝CM，
∴，
解得或，
∴R（，）或（，）；
③当BR，CM为对角线时，BR，CM的中点重合，且BC＝BM，
∴，
解得或，
∴R（，）或（，）；
综上所述，R的坐标为（，）或（，）或（，）或（，）或（，）．