2023年辽宁省各市中考数学试题真题汇编——函数(含答案)

这是一份2023年辽宁省各市中考数学试题真题汇编——函数(含答案)，共58页。试卷主要包含了的图象经过B，C两点等内容，欢迎下载使用。
函数（真题汇编）2023年辽宁省各市中考数学试题全解析版
一．选择题（共8小题）;
1．（2023•沈阳）已知一次函数y＝kx+b的图象如图所示，则k，b的取值范围是（　　）

A．k＞0，b＞0 B．k＞0，b＜0 C．k＜0，b＞0 D．k＜0，b＜0
2．（2023•沈阳）二次函数y＝﹣（x+1）2+2图象的顶点所在的象限是（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
3．（2023•大连）已知蓄电池两端电压U为定值，电流I与R成反比例函数关系．当I＝4A时，R＝10Ω，则当I＝5A时R的值为（　　）
A．6Ω B．8Ω C．10Ω D．12Ω
4．（2023•大连）已知抛物线y＝x2﹣2x﹣1，则当0≤x≤3时，函数的最大值为（　　）
A．﹣2 B．﹣1 C．0 D．2
5．（2023•锦州）如图，在Rt△ABC中，∠ACB＝90°，AC＝3，BC＝4，在△DEF中，DE＝DF＝5，EF＝8，BC与EF在同一条直线上，点C与点E重合．△ABC以每秒1个单位长度的速度沿线段EF所在直线向右匀速运动，当点B运动到点F时，△ABC停止运动．设运动时间为t秒，△ABC与△DEF重叠部分的面积为S，则下列图象能大致反映S与t之间函数关系的是（　　）

A． B．
C． D．
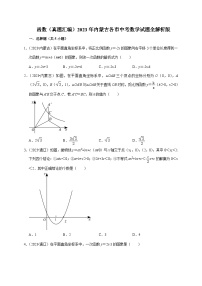
6．（2023•营口）如图，抛物线y＝ax2+bx+c（a≠0）与x轴交于点A（﹣3，0）和点B（1，0），与y轴交于点C．下列说法：①abc＜0；②抛物线的对称轴为直线x＝﹣1；③当﹣3＜x＜0时，ax2+bx+c＞0；④当x＞1时，y随x的增大而增大；⑤am2+bm≤a﹣b（m为任意实数），其中正确的个数是（　　）

A．1个 B．2个 C．3个 D．4个
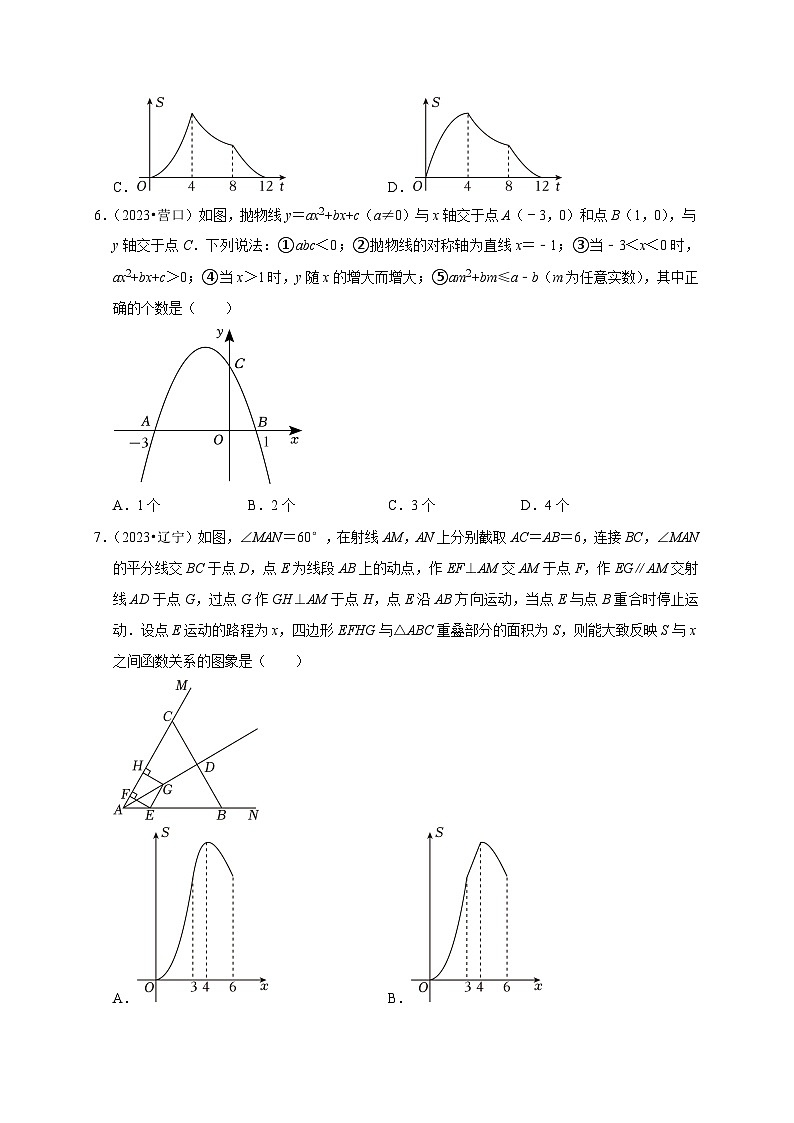
7．（2023•辽宁）如图，∠MAN＝60°，在射线AM，AN上分别截取AC＝AB＝6，连接BC，∠MAN的平分线交BC于点D，点E为线段AB上的动点，作EF⊥AM交AM于点F，作EG∥AM交射线AD于点G，过点G作GH⊥AM于点H，点E沿AB方向运动，当点E与点B重合时停止运动．设点E运动的路程为x，四边形EFHG与△ABC重叠部分的面积为S，则能大致反映S与x之间函数关系的图象是（　　）

A． B．
C． D．
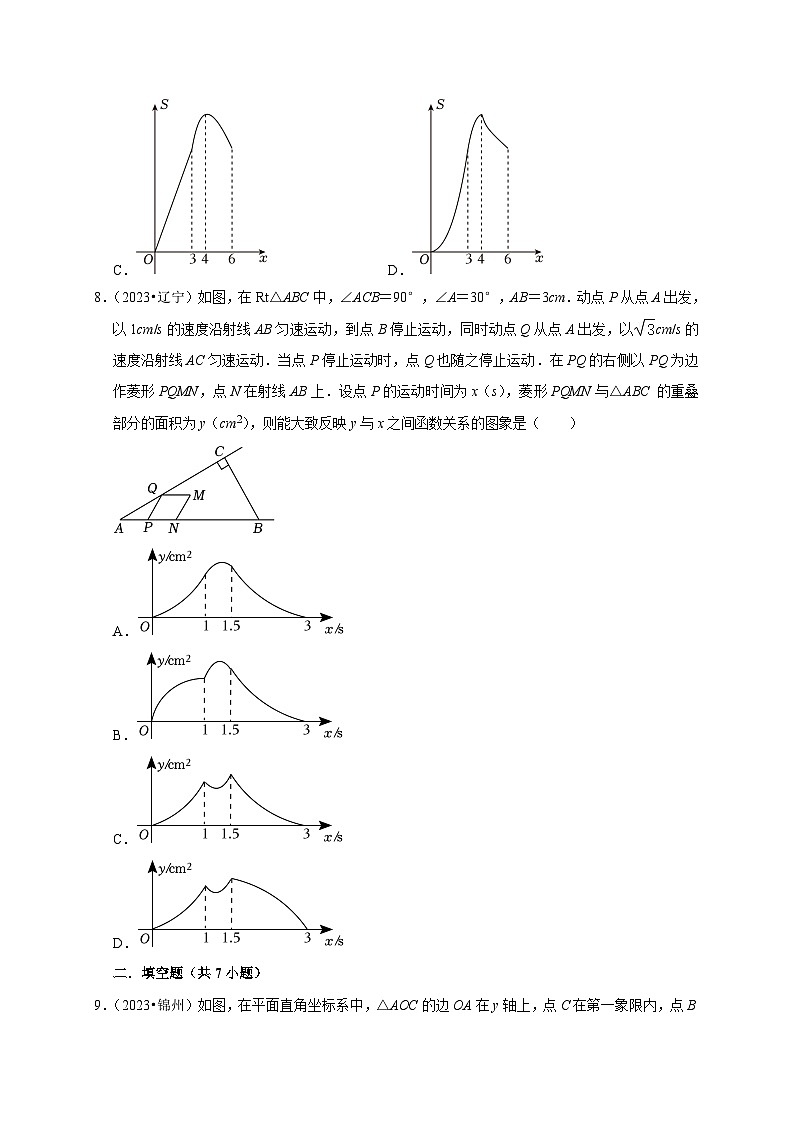
8．（2023•辽宁）如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，AB＝3cm．动点P从点A出发，以1cm/s的速度沿射线AB匀速运动，到点B停止运动，同时动点Q从点A出发，以cm/s的速度沿射线AC匀速运动．当点P停止运动时，点Q也随之停止运动．在PQ的右侧以PQ为边作菱形PQMN，点N在射线AB上．设点P的运动时间为x（s），菱形PQMN与△ABC 的重叠部分的面积为y（cm2），则能大致反映y与x之间函数关系的图象是（　　）

A．
B．
C．
D．
二．填空题（共7小题）
9．（2023•锦州）如图，在平面直角坐标系中，△AOC的边OA在y轴上，点C在第一象限内，点B为AC的中点，反比例函数y＝（x＞0）的图象经过B，C两点．若△AOC的面积是6，则k的值为 　 　．

10．（2023•锦州）如图，在平面直角坐标系中，四边形A1B1B2C1，A2B2B3C2，A3B3B4C3，A4B4B5C4，…都是平行四边形，顶点B1，B2，B3，B4，B5…都在x轴上，顶点C1，C2，C3，C4，…都在正比例函数y＝x（x≥0）的图象上，且B2C1＝2A2C1，B3C2＝2A3C2，B4C3＝2A4C3，…，连接A1B2，A2B3，A3B4，A4B5，…，分别交射线OC1于点O1，O2，O3，O4，…，连接O1A2，O2A3，O3A4，…，得到△O1A2B2，△O2A3B3，△O3A4A4，…若B1（2，0），B2（3，0），A1（3，1），则△O2023A2024B2024的面积为 　 　．

11．（2023•辽宁）如图，在平面直角坐标系中，点A的坐标为（0，2），将线段AO绕点A逆时针旋转120°，得到线段AB，连接OB，点B恰好落在反比例函数y＝（x＞0）的图象上，则k的值是 　 　．
​

12．（2023•沈阳）若点A（﹣2，y1）和点B（﹣1，y2）都在反比例函数y＝的图象上，则y1　 　y2．（用“＜”“＞”或“＝”填空）
13．（2023•沈阳）如图，王叔叔想用长为60m的栅栏，再借助房屋的外墙围成一个矩形羊圈ABCD，已知房屋外墙足够长，当矩形ABCD的边AB＝　 　m时，羊圈的面积最大．

14．（2023•大连）如图，在数轴上，OB＝1，过O作直线l⊥OB于点O，在直线l上截取OA＝2，且A在OC上方．连接AB，以点B为圆心，AB为半径作弧交直线OB于点C，则C点的横坐标为 　 　．

15．（2023•辽宁）如图，矩形ABCD的边AB平行于x轴，反比例函数y＝（x＞0）的图象经过点B，D，对角线CA的延长线经过原点O，且AC＝2AO，若矩形ABCD的面积是8，则k的值为 　 　．

三．解答题（共13小题）
16．（2023•辽宁）电商平台销售某款儿童组装玩具，进价为每件100元，在销售过程中发现，每周的销售量y（件）与每件玩具售价x（元）之间满足一次函数关系（其中100≤x≤160，且x为整数），当每件玩具售价为120元时，每周的销量为80件；当每件玩具售价为140元时，每周的销量为40件．
（1）求y与x之间的函数关系式；
（2）当每件玩具售价为多少元时，电商平台每周销售这款玩具所获的利润最大？最大周利润是多少元？
17．（2023•营口）某大型超市购进一款热销的消毒洗衣液，由于原材料价格上涨，今年每瓶洗衣液的进价比去年每瓶洗衣液的进价上涨4元，今年用1440元购进这款洗衣液的数量与去年用1200元购进这款洗衣液的数量相同，当每瓶洗衣液的现售价为36元时，每周可卖出600瓶，为了能薄利多销，该超市决定降价销售，经市场调查发现，这种洗衣液的售价每降价1元，每周的销量可增加100瓶，规定这种消毒洗衣液每瓶的售价不低于进价．
（1）求今年这款消毒洗衣液每瓶进价是多少元；
（2）当这款消毒洗衣液每瓶的售价定为多少元时，这款洗衣液每周的销售利润最大？最大利润是多少元？
18．（2023•辽宁）商店出售某品牌护眼灯，每台进价为40元，在销售过程中发现，月销量y（台）与销售单价x（元）之间满足一次函数关系，规定销售单价不低于进价，且不高于进价的2倍，其部分对应数据如下表所示：
销售单价x（元）
…
50
60
70
…
月销量y（台）
…
90
80
70
…
（1）求y与x之间的函数关系式；
（2）当护眼灯销售单价定为多少元时，商店每月出售这种护眼灯所获的利润最大？最大月利润为多少元？
19．（2023•锦州）端午节前夕，某批发部购入一批进价为8元/袋的粽子，销售过程中发现：日销量y（袋）与售价x（元/袋）满足如图所示的一次函数关系．
（1）求y与x之间的函数关系式；
（2）每袋粽子的售价定为多少元时，所获日销售利润最大，最大日销售利润是多少元？

20．（2023•大连）如图1，在平面直角坐标系xOy中，直线y＝x与直线BC相交于点A．P（t，0）为线段OB上一动点（不与点B重合），过点P作PD⊥x轴交直线BC于点D，△OAB与△DPB的重叠面积为S，S关于t的函数图象如图2所示．
（1）OB的长为 　 　；△OAB的面积为 　 　；
（2）求S关于t的函数解析式，并直接写出自变量t的取值范围．

21．（2023•辽宁）如图，抛物线y＝﹣x2+bx+c与x轴交于点A和点B（4，0），与y轴交于点C（0，4），点E在抛物线上．

（1）求抛物线的解析式；
（2）点E在第一象限内，过点E作EF∥y轴，交BC于点F，作EH∥x轴，交抛物线于点H，点H在点E的左侧，以线段EF，EH为邻边作矩形EFGH，当矩形EFGH的周长为11时，求线段EH的长；
（3）点M在直线AC上，点N在平面内，当四边形OENM是正方形时，请直接写出点N的坐标．
22．（2023•锦州）如图，抛物线y＝﹣x2+bx+c交x轴于点A（﹣1，0）和B，交y轴于点C（0，3），顶点为D．
（1）求抛物线的表达式；
（2）若点E在第一象限内对称轴右侧的抛物线上，四边形ODEB的面积为7，求点E的坐标；
（3）在（2）的条件下，若点F是对称轴上一点，点H是坐标平面内一点，在对称轴右侧的抛物线上是否存在点G，使以点E，F，G，H为顶点的四边形是菱形，且∠EFG＝60°，如果存在，请直接写出点G的坐标；如果不存在，请说明理由．

23．（2023•沈阳）如图，在平面直角坐标系中，一次函数y＝kx+b的图象交x轴于点A（8，0），交y轴于点B．直线y＝x﹣与y轴交于点D，与直线AB交于点C（6，a）．点M是线段BC上的一个动点（点M不与点C重合），过点M作x轴的垂线交直线CD于点N．设点M的横坐标为m．
（1）求a的值和直线AB的函数表达式；
（2）以线段MN，MC为邻边作▱MNQC，直线QC与x轴交于点E．
①当0≤m＜时，设线段EQ的长度为l，求l与m之间的关系式；
②连接OQ，AQ，当△AOQ的面积为3时，请直接写出m的值．

24．（2023•营口）如图，点A在反比例函数y＝（x＞0）的图象上，AB⊥y轴于点B，tan∠AOB＝，AB＝2．
（1）求反比例函数的解析式；
（2）点C在这个反比例函数图象上，连接AC并延长交x轴于点D，且∠ADO＝45°，求点C的坐标．

25．（2023•辽宁）抛物线y＝ax2+x+c与x轴交于点A和点B（3，0），与y轴交于点C（0，4），点P为第一象限内抛物线上的动点，过点P作PE⊥x轴于点E，交BC于点F．
（1）求抛物线的解析式；
（2）如图1，当△BEF的周长是线段PF长度的2倍时，求点P的坐标；
（3）如图2，当点P运动到抛物线顶点时，点Q是y轴上的动点，连接BQ，过点B作直线l⊥BQ，连接QF并延长交直线l于点M，当BQ＝BM时，请直接写出点Q的坐标．
​
26．（2023•沈阳）如图，在平面直角坐标系中，二次函数y＝x2+bx+c的图象经过点A（0，2），与x轴的交点为点B（，0）和点C．
（1）求这个二次函数的表达式；
（2）点E，G在y轴正半轴上，OG＝2OE，点D在线段OC上，OD＝OE．以线段OD，OE为邻边作矩形ODFE，连接GD，设OE＝a．
①连接FC，当△GOD与△FDC相似时，求a的值；
②当点D与点C重合时，将线段GD绕点G按逆时针方向旋转60°后得到线段GH，连接FH，FG，将△GFH绕点F按顺时针方向旋转α（0°＜α≤180°）后得到△G′FH′，点G，H的对应点分别为G′、H′，连接DE．当△G′FH′的边与线段DE垂直时，请直接写出点H′的横坐标．
27．（2023•大连）如图，在平面直角坐标系中，抛物线C1：y＝x2上有两点A、B，其中点A的横坐标为﹣2，点B的横坐标为1，抛物线C2：y＝﹣x2+bx+c过点A、B．过A作AC∥x轴交抛物线C1另一点为点C．以AC、AC长为边向上构造矩形ACDE．
（1）求抛物线C2的解析式；
（2）将矩形ACDE向左平移m个单位，向下平移n个单位得到矩形A′C′D′E′，点C的对应点C′落在抛物线C1上．
①求n关于m的函数关系式，并直接写出自变量m的取值范围；
②直线A′E′交抛物线C1于点P，交抛物线C2于点Q．当点E′为线段PQ的中点时，求m的值；
③抛物线C2与边E′D′、A′C′分别相交于点M、N，点M、N在抛物线C2的对称轴同侧，当MN＝时，求点C′的坐标．

28．（2023•营口）如图，抛物线y＝ax2+bx﹣1（a≠0）与x轴交于点A（1，0）和点B，与y轴交于点C，抛物线的对称轴交x轴于点D（3，0），过点B作直线l⊥x轴，过点D作DE⊥CD，交直线l于点E．
（1）求抛物线的解析式；
（2）如图，点P为第三象限内抛物线上的点，连接CE和BP交于点Q，当＝时，求点P的坐标；
（3）在（2）的条件下，连接AC，在直线BP上是否存在点F，使得∠DEF＝∠ACD+∠BED？若存在，请直接写出点F的坐标；若不存在，请说明理由．


函数（真题汇编）2023年辽宁省各市中考数学试题全解析版
参考答案与试题解析
一．选择题（共8小题）
1．（2023•沈阳）已知一次函数y＝kx+b的图象如图所示，则k，b的取值范围是（　　）

A．k＞0，b＞0 B．k＞0，b＜0 C．k＜0，b＞0 D．k＜0，b＜0
【答案】B
【解答】解：由图可知该一次函数图象经过第一、三、四象限，
则k＞0，b＜0．
故答案为B．
2．（2023•沈阳）二次函数y＝﹣（x+1）2+2图象的顶点所在的象限是（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
【答案】B
【解答】解：∵y＝﹣（x+1）2+2，
∴顶点坐标为（﹣1，2），
∴顶点在第二象限．
故选：B．
3．（2023•大连）已知蓄电池两端电压U为定值，电流I与R成反比例函数关系．当I＝4A时，R＝10Ω，则当I＝5A时R的值为（　　）
A．6Ω B．8Ω C．10Ω D．12Ω
【答案】B
【解答】解：设I＝，则U＝IR＝40，
∴R＝＝＝8，
故选：B．
4．（2023•大连）已知抛物线y＝x2﹣2x﹣1，则当0≤x≤3时，函数的最大值为（　　）
A．﹣2 B．﹣1 C．0 D．2
【答案】D
【解答】解：∵y＝x2﹣2x﹣1＝（x﹣1）2﹣2，
∴对称轴为直线x＝1，
∵a＝1＞0，
∴抛物线的开口向上，
∴当0≤x＜1时，y随x的增大而减小，
∴当x＝0时，y＝﹣1，
当1≤x≤3时，y随x的增大而增大，
∴当x＝3时，y＝9﹣6﹣1＝2，
∴当0≤x≤3时，函数的最大值为2，
故选：D．
5．（2023•锦州）如图，在Rt△ABC中，∠ACB＝90°，AC＝3，BC＝4，在△DEF中，DE＝DF＝5，EF＝8，BC与EF在同一条直线上，点C与点E重合．△ABC以每秒1个单位长度的速度沿线段EF所在直线向右匀速运动，当点B运动到点F时，△ABC停止运动．设运动时间为t秒，△ABC与△DEF重叠部分的面积为S，则下列图象能大致反映S与t之间函数关系的是（　　）

A． B．
C． D．
【答案】A
【解答】解：过点D作DH⊥CB于H，

∵DE＝DF＝5，EF＝8，
∴EH＝FH＝EF＝4，
∴DH＝＝3，
当0≤t＜4时，
如图，重叠部分为△EPQ，此时EQ＝t，PQ∥DH，

∴△EPQ∽△EDH，
∴，即，
∴PQ＝t，
∴S＝＝2，
当4≤t＜8时，
如图，重叠部分为四边形POC′B′，此时BB′＝CC′＝t，PB∥DE．

∴B′F＝BC+CF﹣BB′＝12﹣t，FC＝8﹣t，
∵PB∥DE，
∴△PBF∽△DCF，
∴，
又S△DCF＝，
∴，
∵DH⊥BC．∠AB′C′＝90°，
∴AC′∥DH，
∴△C′QF∽△HFD．
∴，即，
∴，
∴S＝S△PB′F﹣S△C′QF＝＝，
当8≤t≤12时
如图，重叠部分为四边形△PFB′，此时BB′＝CC′＝t，PB′∥DE．

∴B′F＝BC+CF﹣BB′＝12﹣t，
∵PB′∥DE．
∴△PB′F∽△DCF，
∴，即，
∴，S＝S△PB′F＝，
综上，
∴符合题意的函数图象是选项A．
故选：A．
6．（2023•营口）如图，抛物线y＝ax2+bx+c（a≠0）与x轴交于点A（﹣3，0）和点B（1，0），与y轴交于点C．下列说法：①abc＜0；②抛物线的对称轴为直线x＝﹣1；③当﹣3＜x＜0时，ax2+bx+c＞0；④当x＞1时，y随x的增大而增大；⑤am2+bm≤a﹣b（m为任意实数），其中正确的个数是（　　）

A．1个 B．2个 C．3个 D．4个
【答案】C
【解答】解：∵抛物线开口向下，
∴a＜0，
∵抛物线y＝ax2+bx+c（a≠0）与x轴交于点A（﹣3，0）和点B（1，0），
∴对称轴为直线x＝＝﹣1，故②正确；
∴﹣＝﹣1，
∴b＝2a＜0，
∵与y轴的交点在正半轴上，
∴c＞0，
∴abc＞0，故①错误；
由图象可知，当﹣3＜x＜0时，y＞0，
∴当﹣3＜x＜0时，ax2+bx+c＞0，故③正确；
由图象可知，当x＞1时，y随x的增大而减小，故④错误；
∵抛物线的对称轴为直线x＝﹣1，
∴当x＝﹣1时，函数有最大值，
∴当m为任意实数时，am2+bm+c≤a﹣b+c，
∴am2+bm≤a﹣b，故⑤正确；
综上所述，结论正确的是②③⑤共3个．
故选：C．
7．（2023•辽宁）如图，∠MAN＝60°，在射线AM，AN上分别截取AC＝AB＝6，连接BC，∠MAN的平分线交BC于点D，点E为线段AB上的动点，作EF⊥AM交AM于点F，作EG∥AM交射线AD于点G，过点G作GH⊥AM于点H，点E沿AB方向运动，当点E与点B重合时停止运动．设点E运动的路程为x，四边形EFHG与△ABC重叠部分的面积为S，则能大致反映S与x之间函数关系的图象是（　　）

A． B．
C． D．
【答案】A
【解答】解：∵∠MAN＝60°，AC＝AB＝6，
∴△ABC是边长为6的正三角形，
∵AD平分∠MAN，
∴∠MAD＝∠NAD＝30°，AD⊥BC，CD＝DB＝3，
①当矩形EFHG全部在△ABC之中，即由图1到图2，此时0＜x≤3，
∵EG∥AC，
∴∠NAD＝∠AGE＝30°，
∴AE＝EG＝x，
在Rt△AEF中，AE＝x，∠EAF＝60°，
∴EF＝AE＝x，
∴S＝x2；
②图3时，AE+AF＝AC，即x+x＝6，解得x＝4，由图2到图3，此时3＜x≤4，
如图4，由题意可知△EQB是正三角形，
∴EQ＝EB＝BQ＝6﹣x，
∴GQ＝x﹣（6﹣x）＝2x﹣6，
∴S＝S矩形EFHG﹣S△PQG
＝x2﹣×（2x﹣6）2
＝﹣x2+12x﹣18，
③图6时，x＝6，由图3到图6，此时4＜x≤6，
如图5，由题意可知△EKB是正三角形，
∴EK＝EB＝BK＝6﹣x，FC＝AC﹣AF＝6﹣x，EF＝x，
∴S＝S梯形EFCK
＝（6﹣x+6﹣x）×x
＝﹣x2+3x，
综上所述，S与x的函数关系式为S＝，
因此三段函数的都是二次函数关系，其中第1段是开口向上，第2段、第3段是开口向下的抛物线，
故选：A．






8．（2023•辽宁）如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，AB＝3cm．动点P从点A出发，以1cm/s的速度沿射线AB匀速运动，到点B停止运动，同时动点Q从点A出发，以cm/s的速度沿射线AC匀速运动．当点P停止运动时，点Q也随之停止运动．在PQ的右侧以PQ为边作菱形PQMN，点N在射线AB上．设点P的运动时间为x（s），菱形PQMN与△ABC 的重叠部分的面积为y（cm2），则能大致反映y与x之间函数关系的图象是（　　）

A．
B．
C．
D．
【答案】A
【解答】解：作PD⊥AC于点D，作QE⊥AB于点E，

由题意得AP＝x，AQ＝x，
∴AD＝AP•cos30°＝x，
∴AD＝DQ＝AQ，
∴PD是线段AQ的垂直平分线，
∴∠PQA＝∠A＝30°，
∴∠QPE＝60°，PQ＝AP＝x，
∴QE＝AQ＝x，PQ＝PN＝MN＝QM＝x，
当点M运动到直线BC上时，

此时，△BMN是等边三角形，
∴AP＝PN＝BN＝AB＝1，x＝1；
当点Q、N运动到与点C，B重合时，

∴AP＝PN＝AB＝，x＝；
当点P运动到与点B重合时，
∴AP＝AB＝3，x＝3；
∴当0＜x≤1时，y＝x•x＝x2，
当1＜x≤时，如图，作FG⊥AB于点G，交QM于点R，

则BN＝FN＝FB＝3﹣2x，FM＝MS＝FS＝3x﹣3，FR＝（3x﹣3），
∴y＝x2﹣（3x﹣3）•（3x﹣3）＝﹣x2+x﹣，
当＜x＜3时，如图，作HI⊥AB于点I，

则BP＝PH＝HB＝3﹣x，HI＝（3﹣x），
∴y＝•（3﹣x）•（3﹣x）＝x2﹣x+，
综上，y与x之间函数关系的图象分为三段，当0＜x≤1时，是开口向上的一段抛物线，当1＜x≤时，是开口向下的一段抛物线，当＜x＜3时，是开口向上的一段抛物线，
只有选项A符合题意，
故选：A．
二．填空题（共7小题）
9．（2023•锦州）如图，在平面直角坐标系中，△AOC的边OA在y轴上，点C在第一象限内，点B为AC的中点，反比例函数y＝（x＞0）的图象经过B，C两点．若△AOC的面积是6，则k的值为 　4　．

【答案】4．
【解答】解：过点C作CD⊥y轴于点D，如图：

设点C的坐标为（a，b），点A的坐标为（0，c），
∴CD＝a，OA＝c，
∵△AOC的面积是6，
∴，
∴ac＝12，
∵点C（a，b）在反比例函数（x＞0）的图象上，
∴k＝ab，
∵点B为AC的中点，
∴点，
∵点B在反比例函数（x＞0）的图象上，
∴，
即：4k＝a（b+c），
∴4k＝ab+ac，
将ab＝k，ac＝12代入上式得：k＝4．
故答案为：4．
10．（2023•锦州）如图，在平面直角坐标系中，四边形A1B1B2C1，A2B2B3C2，A3B3B4C3，A4B4B5C4，…都是平行四边形，顶点B1，B2，B3，B4，B5…都在x轴上，顶点C1，C2，C3，C4，…都在正比例函数y＝x（x≥0）的图象上，且B2C1＝2A2C1，B3C2＝2A3C2，B4C3＝2A4C3，…，连接A1B2，A2B3，A3B4，A4B5，…，分别交射线OC1于点O1，O2，O3，O4，…，连接O1A2，O2A3，O3A4，…，得到△O1A2B2，△O2A3B3，△O3A4A4，…若B1（2，0），B2（3，0），A1（3，1），则△O2023A2024B2024的面积为 　　．

【答案】．
【解答】解：∵B2（3，0），A1（3，1）
∴O1（3，），A1B2⊥x轴，
同理可得：A2B3⊥x轴，A3B4⊥x轴，
可得：△A1B1B2∽△A2B2B3，
∴，
∵A1B1＝B2C1，
∴，
∴B2B3＝，
∴＝O1B2•B2B3＝，
可得：△O2A3B3∽△O1A2B2，
∴S_△O2A3B3：＝（A3B3：A2B2）2，
∴＝（）2，
.....．
S_△O2023A2024B2024＝（）2023﹣1＝，
故答案为：．
11．（2023•辽宁）如图，在平面直角坐标系中，点A的坐标为（0，2），将线段AO绕点A逆时针旋转120°，得到线段AB，连接OB，点B恰好落在反比例函数y＝（x＞0）的图象上，则k的值是 　　．
​

【答案】．
【解答】解：过点B作BC⊥y轴于点C，
由旋转的性质得，AO＝AB，∠OAB＝120°，
∵点A的坐标为（0，2），
∴AO＝2，
∴AB＝2，
∵∠OAB＝120°，
∴∠BAC＝180°﹣∠OAB＝180°﹣120°＝60°，
∴∠ABC＝90°﹣∠BAC＝30°，
∴，
由勾股定理得，
∴OC＝AO+AC＝2+1＝3，
∴点B的坐标为，
∵点B恰好落在反比例函数（x＞0）的图象上，
∴，
故答案为：．

12．（2023•沈阳）若点A（﹣2，y1）和点B（﹣1，y2）都在反比例函数y＝的图象上，则y1　＞　y2．（用“＜”“＞”或“＝”填空）
【答案】＞．
【解答】解：令x＝﹣2，
则，
令x＝﹣1，
则，
∵﹣1＞﹣2，
∴y1＞y2，
故答案为：＞．
13．（2023•沈阳）如图，王叔叔想用长为60m的栅栏，再借助房屋的外墙围成一个矩形羊圈ABCD，已知房屋外墙足够长，当矩形ABCD的边AB＝　15　m时，羊圈的面积最大．

【答案】15．
【解答】解：设AB为xm，面积为Sm2，
由题意可得：S＝x（60﹣2x）＝﹣2（x﹣15）2+450，
∴当x＝15时，S取得最大值，
即AB＝15m时，羊圈的面积最大，
故答案为：15．
14．（2023•大连）如图，在数轴上，OB＝1，过O作直线l⊥OB于点O，在直线l上截取OA＝2，且A在OC上方．连接AB，以点B为圆心，AB为半径作弧交直线OB于点C，则C点的横坐标为 　1+　．

【答案】1+，
【解答】解：∵OA⊥OB，
∴∠AOB＝90°，
在Rt△AOB中，AB＝＝＝，
∵以点B为圆心，AB为半径作弧交直线OB于点C，
∴AB＝BC＝，
∴OC＝OB+BC＝1+，
∴点C的横坐标为1+．
故答案为：1+，
15．（2023•辽宁）如图，矩形ABCD的边AB平行于x轴，反比例函数y＝（x＞0）的图象经过点B，D，对角线CA的延长线经过原点O，且AC＝2AO，若矩形ABCD的面积是8，则k的值为 　6　．

【答案】6．
【解答】解：如图，延长CD交y轴于E，连接OD，
∵矩形ABCD的面积是8，
∴S△ADC＝4，
∵AC＝2AO，
∴S△ADO＝2，
∵AD∥OE，
∴△ACD∽△OCE，
∴AD：OE＝AC：OC＝2：3，
∴S△ODE＝3，
由几何意义得，＝3，
∵k＞0，
∴k＝6，
故答案为：6．

三．解答题（共13小题）
16．（2023•辽宁）电商平台销售某款儿童组装玩具，进价为每件100元，在销售过程中发现，每周的销售量y（件）与每件玩具售价x（元）之间满足一次函数关系（其中100≤x≤160，且x为整数），当每件玩具售价为120元时，每周的销量为80件；当每件玩具售价为140元时，每周的销量为40件．
（1）求y与x之间的函数关系式；
（2）当每件玩具售价为多少元时，电商平台每周销售这款玩具所获的利润最大？最大周利润是多少元？
【答案】见试题解答内容
【解答】解：（1）设y与x之间的函数关系式为y＝kx+b，
∵当每件玩具售价为120元时，每周的销量为80件；当每件玩具售价为140元时，每周的销量为40件，
∴，
解得，
即y与x之间的函数关系式为y＝﹣2x+320；
（2）设利润为w元，
由题意可得：w＝（x﹣100）（﹣2x+320）＝﹣2（x﹣130）2+1800，
∴当x＝130时，w取得最大值，此时w＝1800，
答：当每件玩具售价为130元时，电商平台每周销售这款玩具所获的利润最大，最大周利润是1800元．
17．（2023•营口）某大型超市购进一款热销的消毒洗衣液，由于原材料价格上涨，今年每瓶洗衣液的进价比去年每瓶洗衣液的进价上涨4元，今年用1440元购进这款洗衣液的数量与去年用1200元购进这款洗衣液的数量相同，当每瓶洗衣液的现售价为36元时，每周可卖出600瓶，为了能薄利多销，该超市决定降价销售，经市场调查发现，这种洗衣液的售价每降价1元，每周的销量可增加100瓶，规定这种消毒洗衣液每瓶的售价不低于进价．
（1）求今年这款消毒洗衣液每瓶进价是多少元；
（2）当这款消毒洗衣液每瓶的售价定为多少元时，这款洗衣液每周的销售利润最大？最大利润是多少元？
【答案】（1）今年这款消毒洗衣液每瓶进价是24元；
（2）当这款消毒洗衣液每瓶的售价定为33元时，这款洗衣液每周的销售利润最大，最大利润是8100元．
【解答】解：（1）设今年这款消毒洗衣液每瓶进价是m元，
根据题意得：＝，
解得m＝24，
经检验，m＝24是原方程的解，也符合题意，
∴今年这款消毒洗衣液每瓶进价是24元；
（2）设消毒洗衣液每瓶的售价为x元，每周的销售利润为w元，
根据题意得w＝（x﹣24）[600+100（36﹣x）]＝﹣100x2+6600x﹣100800＝﹣100（x﹣33）2+8100，
∵﹣100＜0，
∴当x＝33时，w取最大值8100，
∴当这款消毒洗衣液每瓶的售价定为33元时，这款洗衣液每周的销售利润最大，最大利润是8100元．
18．（2023•辽宁）商店出售某品牌护眼灯，每台进价为40元，在销售过程中发现，月销量y（台）与销售单价x（元）之间满足一次函数关系，规定销售单价不低于进价，且不高于进价的2倍，其部分对应数据如下表所示：
销售单价x（元）
…
50
60
70
…
月销量y（台）
…
90
80
70
…
（1）求y与x之间的函数关系式；
（2）当护眼灯销售单价定为多少元时，商店每月出售这种护眼灯所获的利润最大？最大月利润为多少元？
【答案】见试题解答内容
【解答】解：（1）设月销量y（台）与销售单价x（元）之间满足一次函数关系式为y＝kx+b，
把（50，90）和（60，80）代入得，
解得，
∴y＝﹣x+140；
（2）∵规定销售单价不低于进价，且不高于进价的2倍，
∴40≤x≤80，
设每月出售这种护眼灯所获的利润为w元，
根据题意得，w＝（x﹣40）y＝（x﹣40）（﹣x+140）＝﹣x2+180x﹣5600＝﹣（x﹣90）2+2500，
∴当护眼灯销售单价定为80元时，商店每月出售这种护眼灯所获的利润最大，最大月利润为2400元．
19．（2023•锦州）端午节前夕，某批发部购入一批进价为8元/袋的粽子，销售过程中发现：日销量y（袋）与售价x（元/袋）满足如图所示的一次函数关系．
（1）求y与x之间的函数关系式；
（2）每袋粽子的售价定为多少元时，所获日销售利润最大，最大日销售利润是多少元？

【答案】（1）y与x的函数关系式为y＝﹣40x+680；
（2）当粽子的售价定为12.5元/袋时，日销售利润最大，最大日销售利润是810元．
【解答】解：（1）设y与x的函数关系式为y＝kx+b，
把x＝10，y＝280和x＝14，y＝120别代入解析式，
得 ，
解得，
∴y与x的函数关系式为y＝﹣40x+680；
（2）设这种粽子日销售利润为w元，
则w＝（x﹣8）（﹣40x+680）
＝40x2+1000x﹣5440
＝40（x﹣）2+810，
∵﹣40＜0，抛物线开口向下，
∴x＝12.5时，w有最大值，最大值为810，
答：当粽子的售价定为12.5元/袋时，日销售利润最大，最大日销售利润是810元．
20．（2023•大连）如图1，在平面直角坐标系xOy中，直线y＝x与直线BC相交于点A．P（t，0）为线段OB上一动点（不与点B重合），过点P作PD⊥x轴交直线BC于点D，△OAB与△DPB的重叠面积为S，S关于t的函数图象如图2所示．
（1）OB的长为 　4　；△OAB的面积为 　　；
（2）求S关于t的函数解析式，并直接写出自变量t的取值范围．

【答案】（1）4，；
（2）S＝．
【解答】解：（1）t＝0时，P与O重合，此时S＝S△ABO＝，
t＝4时，S＝0，P与B重合，
∴OB＝4，B（4，0），
故答案为：4，；
（2）∵A在直线y＝x上，
∴∠AOB＝45°，
设A（a，a），
∴S△ABO＝OB•a，即×4a＝，
∴a＝，
∴A（，）；
当0≤t≤时，设OA交PD于E，如图：

∵∠AOB＝45°，PD⊥OB，
∴△PEO是等腰直角三角形，
∴PE＝PO＝t，
∴S△POE＝t2，
∴S＝﹣S△POE＝﹣t2；
当＜t＜4时，如图：

由A（，），B（4，0）得直线AB解析式为y＝﹣x+2，
当x＝0时，y＝2，
∴C（0，2），
∴OC＝2，
∵tan∠CBO＝＝＝＝，
∴DP＝PB＝（4﹣t）＝2﹣t，
∴S＝S△DPB＝DP•PB＝（2﹣t）×（4﹣t）＝（4﹣t）2＝t2﹣2t+4；
综上所述，S＝．
21．（2023•辽宁）如图，抛物线y＝﹣x2+bx+c与x轴交于点A和点B（4，0），与y轴交于点C（0，4），点E在抛物线上．

（1）求抛物线的解析式；
（2）点E在第一象限内，过点E作EF∥y轴，交BC于点F，作EH∥x轴，交抛物线于点H，点H在点E的左侧，以线段EF，EH为邻边作矩形EFGH，当矩形EFGH的周长为11时，求线段EH的长；
（3）点M在直线AC上，点N在平面内，当四边形OENM是正方形时，请直接写出点N的坐标．
【答案】（1）见解答．
（2）EH＝4，
（3）点N的坐标为（4，4）或（﹣，）或（，）或（，）．
【解答】解：（1）∵抛物线y＝﹣x2+bx+c经过点B（4，0）和C（0，4），
∴
解得，
∴抛物线的解析式为y＝﹣x2+x+4；
（2）∵点B（4，0）和C（0，4）．
设直线BC的解析式为v＝kx+4，则0＝4k+4，
解得k＝﹣1．
直线BC的解析式为y＝﹣x+4，
设E（x，﹣x2+x+4），且0＜x＜4，则F（x，﹣x+4），
GH﹣EF＝﹣x2+x+4﹣（﹣x+4）＝﹣x2+2x，
∴解析式的对称轴为﹣，
∴H（2﹣x，﹣x2+x+4），
∴GF﹣EH＝x﹣（4﹣x）＝2x﹣2，
依题意得2（﹣x2+2x+2x﹣2）＝11．
解得x＝5（舍去）或x＝3．
∴EH＝4，
（3）令y＝0，则﹣x2+x+4＝0，
解得x＝﹣2或x＝4．
∴A（﹣2，0）．
同理，直线AC的解析式为y＝2x+4，
∵四边形OENM是正方形，
∴OE＝OM，∠EOM＝90°，分别过点M、E作y轴的垂线，垂足分别为P、Q，如图，

∠OPM＝∠EQO＝90°，∠OMP＝90°﹣∠MOP＝∠EOQ．
∴△OMP≌Δ EOQ（AAS）．
∴PM＝OQ，PO＝EQ．
设E（m，﹣m2+m+4），
∴PM＝OQ＝﹣m，PO﹣EQ＝﹣m2+m+4．
则M（m2﹣m+4，m），
∵点M在直线AC上，
∴m＝2（﹣m﹣4）+4．
解得m＝4或m＝﹣1
当m＝4时，M（0，4），E（4，0），
即点M与点C重合，点E与点B重合时，四边形OENM是正方形，此时N（4，4）：
当m＝﹣1时，M（﹣，﹣1），E（﹣1，），
点O向左平移个单位，再向下平移1个单位，得到点M，
则点E向左平移个单位，再向下平移1个单位，得到点N，
N（﹣1﹣，﹣1），即N（﹣，）．
当OM沿着点O逆时针旋转90°得到OE，如图：

设M（a，b），则点E（b，﹣a），
∵点M在y＝2x+4，
∴b＝2a+4，则点M（a，2a+4），
此时点E（2a+4，﹣a），
点E在y＝﹣x2+x+4的图象上，
∴，
解得a＝0或﹣，
∴M1 （0，4），E1 （4，0），M2（﹣，﹣1），E2（﹣1，），
当点E为点M绕点O逆时针旋转90°时，点E（﹣b，a），
M（a，2a+4），E（﹣2a﹣4，a），
点E在y＝﹣x2+x+4的图象上，
∴﹣（﹣2a﹣4）2﹣2a﹣4+4＝a，
解得a＝，
∴M1（，），E1（，），
M2（，），E2（，），
∴点N的坐标为（，）或（，），
综上，点N的坐标为（4，4）或（﹣，）或（，）或（，）．
22．（2023•锦州）如图，抛物线y＝﹣x2+bx+c交x轴于点A（﹣1，0）和B，交y轴于点C（0，3），顶点为D．
（1）求抛物线的表达式；
（2）若点E在第一象限内对称轴右侧的抛物线上，四边形ODEB的面积为7，求点E的坐标；
（3）在（2）的条件下，若点F是对称轴上一点，点H是坐标平面内一点，在对称轴右侧的抛物线上是否存在点G，使以点E，F，G，H为顶点的四边形是菱形，且∠EFG＝60°，如果存在，请直接写出点G的坐标；如果不存在，请说明理由．

【答案】（1）y＝﹣x2+2x+3；
（2）E（2，3）；
（3）存在，G的坐标为（，）或（，）．
【解答】解：（1）∵抛物线y＝﹣x2+bx+c过点A（﹣1，0）和点C（0，3），
∴，
∴，
∴抛物线的表达式y＝﹣x2+2x+3．
（2）设抛物线的对称轴与x轴交于点M，过点E作EN⊥x轴于点N，
设E（x，﹣x2+2x+3），
∴BN＝3﹣x，MN＝x﹣1，
∴S四边形ODEB＝S△ODM+S梯形DMNE+S△ENB＝×1×4+（4﹣x2+4x+3）（x﹣1）+（﹣x2+2x+3）（3﹣x）＝﹣x2+4x+3，
∵四边形ODEB的面积为7，
∴﹣x2+4x+3＝7，
∴x2﹣4x+4＝0，
∴x1＝x2＝2，
∴E（2，3）．

（3）存在点G，使以点E，F，G，H为顶点的四边形是菱形，且∠EFG＝60°，满足条件G的坐标为（，）或（，）．理由如下：
如图，连接CG，DG，
∵四边形EFGH是菱形，且∠EFG＝60°，
∴△EFG是等边三角形，
∴△DCE是等边三角形，
∴△CEG≌△DEF，
∴∠ECG＝∠EDF＝30°，
∴直线CG的表达式为y＝﹣x+3，
∴，
∴G（，）；

如图，连接CG、DG、CF，
∵四边形EFGH是菱形，且∠EFG＝60°，
∴△EFG是等边三角形，
∴△DCE是等边三角形，
∴△DGE≌△CFE，
∴DG＝CF，
∴CF＝FE，GE＝FE，
∴DG＝GE，
∴△CDG≌△CEG，
∴∠DCG＝∠ECG＝30°，
∴直线CG的表达式为y＝x+3，
∴，
∴G（，），

综上，G（，）或（，）．
23．（2023•沈阳）如图，在平面直角坐标系中，一次函数y＝kx+b的图象交x轴于点A（8，0），交y轴于点B．直线y＝x﹣与y轴交于点D，与直线AB交于点C（6，a）．点M是线段BC上的一个动点（点M不与点C重合），过点M作x轴的垂线交直线CD于点N．设点M的横坐标为m．
（1）求a的值和直线AB的函数表达式；
（2）以线段MN，MC为邻边作▱MNQC，直线QC与x轴交于点E．
①当0≤m＜时，设线段EQ的长度为l，求l与m之间的关系式；
②连接OQ，AQ，当△AOQ的面积为3时，请直接写出m的值．

【答案】（1）a的值为，直线AB解析式为y＝﹣x+6；
（2）①l＝；
②或．
【解答】解：（1）∵点C（6，a）在直线y＝x﹣上，
∴a＝＝，
∵一次函数y＝kx+b的图象过点A（8，0）和点C（6，），
∴，
解得，
∴直线AB的解析式为y＝﹣x+6；
（2）①∵M点在直线y＝﹣x+6上，且M的横坐标为m，
∴M的纵坐标为：﹣m+6，
∵N点在直线y＝x﹣上，且N点的横坐标为m，
∴N点的纵坐标为：m﹣，
∴|MN|＝﹣m+6﹣m+＝﹣，
∵点C（6，），线段EQ的长度为l，
∴|CQ|＝1+，
∵|MN|＝|CQ|，
∴﹣＝1+，
即l＝；
②∵△AOQ的面积为3，
∴OA•EQ＝3，
即，
解得EQ＝，
由①知，EQ＝6﹣，
∴|6﹣|＝，
解得m＝或，
即m的值为或．
24．（2023•营口）如图，点A在反比例函数y＝（x＞0）的图象上，AB⊥y轴于点B，tan∠AOB＝，AB＝2．
（1）求反比例函数的解析式；
（2）点C在这个反比例函数图象上，连接AC并延长交x轴于点D，且∠ADO＝45°，求点C的坐标．

【答案】（1）反比例函数的解析式为y＝；
（2）C（4，2）．
【解答】解：（1）∵AB⊥y轴于点B，
∴∠OBA＝90°，
在Rt△OBA中，AB＝2，tan∠AOB＝，
∴OB＝4，
∴A（2，4），
∵点A在反比例函数y＝（x＞0）的图象上，
∴k＝4×2＝8；
∴反比例函数的解析式为y＝；
（2）如图，过A作AF⊥x轴于F，
∴∠AFD＝90°，
∵∠ADO＝45°，
∴∠FAD＝90°﹣∠CDE＝45°，
∴AF＝DF＝OB＝4，
∵OF＝AB＝2，
∴OD＝6，
∴D（6，0），
设直线AC的解析式为y＝ax+b，
∵点A（2，4），D（6，0）在直线AC上，
∴，
∴，
∴直线AC的解析式为y＝﹣x+6①，
由（1）知，反比例函数的解析式为y＝②，
联立①②解得，或，
∴C（4，2）．

25．（2023•辽宁）抛物线y＝ax2+x+c与x轴交于点A和点B（3，0），与y轴交于点C（0，4），点P为第一象限内抛物线上的动点，过点P作PE⊥x轴于点E，交BC于点F．
（1）求抛物线的解析式；
（2）如图1，当△BEF的周长是线段PF长度的2倍时，求点P的坐标；
（3）如图2，当点P运动到抛物线顶点时，点Q是y轴上的动点，连接BQ，过点B作直线l⊥BQ，连接QF并延长交直线l于点M，当BQ＝BM时，请直接写出点Q的坐标．
​
【答案】（1）y＝﹣x2+x+4；
（2）P（，5）；
（3）Q（0，+）或（0，﹣）．
【解答】解：（1）将点B（3，0），点C（0，4）代入y＝ax2+x+c，
∴，
解得，
∴抛物线的解析式为y＝﹣x2+x+4；
（2）∵点B（3，0），点C（0，4），
∴OB＝3，OC＝4，
∴tan∠OBC＝，
∴BE＝EF，BF＝EF，
∴△BEF的周长＝3EF，
∵△BEF的周长是线段PF长度的2倍，
∴3EF＝2PF，
设直线BC的解析式为y＝kx+4，
∴3k+4＝0，
解得k＝﹣，
∴直线BC的解析式为y＝﹣x+4，
设P（t，﹣t2+t+4），则F（t，﹣t+4），E（t，0），
∴EF＝﹣t+4，PF＝﹣t2+t+4+t﹣4＝﹣t2+4t，
∴3（﹣t+4）＝2（﹣t2+4t），
解得t＝3（舍）或t＝，
∴P（，5）；
（3）∵y＝﹣x2+x+4＝﹣（x﹣1）2+，
∴P（1，），
∵FP⊥x轴，
∴F（1，），
设Q（0，n），
过点M作MN⊥x轴交于点N，
∵∠QBM＝90°，
∴∠QBO+∠MBN＝90°，
∵∠QBO+∠OQB＝90°，
∴∠MBN＝∠OQB，
∵BQ＝BM，
∴△BQO≌△MBN（AAS），
∴QO＝BN，MN＝OB，
∴M（3+n，3），
设直线QM的解析式为y＝k'x+n，
∴k'（3+n）+n＝3，
解得k'＝，
∴直线QM的解析式为y＝x+n，
将点F代入，+n＝，
解得n＝+或n＝﹣，
∴Q（0，+）或（0，﹣）．

26．（2023•沈阳）如图，在平面直角坐标系中，二次函数y＝x2+bx+c的图象经过点A（0，2），与x轴的交点为点B（，0）和点C．
（1）求这个二次函数的表达式；
（2）点E，G在y轴正半轴上，OG＝2OE，点D在线段OC上，OD＝OE．以线段OD，OE为邻边作矩形ODFE，连接GD，设OE＝a．
①连接FC，当△GOD与△FDC相似时，求a的值；
②当点D与点C重合时，将线段GD绕点G按逆时针方向旋转60°后得到线段GH，连接FH，FG，将△GFH绕点F按顺时针方向旋转α（0°＜α≤180°）后得到△G′FH′，点G，H的对应点分别为G′、H′，连接DE．当△G′FH′的边与线段DE垂直时，请直接写出点H′的横坐标．
【答案】（1）y＝﹣x+2；（2）①或；②当△G′FH′的边与线段DE垂直时，点H′的横坐标为2+3或2+或．
【解答】解：（1）∵二次函数y＝x2+bx+c的图象经过点A（0，2），与x轴的交点为点B（，0），
∴，
解得：，
∴此抛物线的解析式为y＝﹣x+2；
（2）①令y＝0，则﹣x+2＝0，
解得：x＝或x＝2，
∴C（2，0），
∴OC＝2．
∵OE＝a，OG＝2OE，OD＝OE，
∴OG＝2a，OD＝a．
∵四边形ODFE为矩形，
∴EF＝OD＝a，FD＝OE＝a，
∴E（0，a），D（a，0），F（a，a），G（0，2a），
∴CD＝OC﹣OD＝2﹣a．
Ⅰ．当△GOD∽△FDC时，
∴，
∴，
∴a＝；
Ⅱ．当△GOD∽△CDF时，
∴，
∴，
∴a＝．
综上，当△GOD与△FDC相似时，a的值为或；
②∵点D与点C重合，
∴OD＝OC＝2．
∴OE＝2，OG＝2OE＝4，EF＝OD＝2，DF＝OE＝2，
∴EG＝OE＝2．

∴EG＝DF＝2，
∵EG∥DF，
∴四边形GEDF为平行四边形，
∴FG＝DE＝＝＝4，
∴∠GFE＝30°，
∴∠EGF＝60°，
∵∠DGH＝60°，
∴∠EGF＝∠DGH，
∴∠OGD＝∠FGH．
在△GOD和△GFH中，
，
∴△GOD≌△GFH（SAS），
∴FH＝OD＝2，∠GOD＝∠GFH＝90°．
∴GH＝＝＝2．
Ⅰ．当G′F所在直线与DE垂直时，如图，

∵∠GFH＝90°，GF∥DE，
∴∠G′FH′＝90°，
∴G，F，H′三点在一条直线上，
∴GH′＝GF+FH′＝FG+FH＝4+2．
过点H′作H′K⊥y轴于点K，则H′K∥FE，
∴∠KH′G＝∠EFG＝30°，
∴H′K＝H′G•cos30°＝×（4+2）＝2+3，
∴此时点H′的横坐标为2+3；
Ⅱ．当G′H′所在直线与DE垂直时，如图，

∵GF∥DE，
∴G′H′⊥GF，
设GF的延长线交G′H′于点M，过点M作MP⊥EF，交EF的延长线于点P，过点H′作H′N⊥MP，交PM的延长线于点N，则H′N∥PF∥x轴，∠PFM＝∠EFG＝30°．
∵G′H′•FM＝FH′•FG′，
∴4×2＝2FM，
∴FM＝．
∴FP＝FM•cos30°＝＝，
∴PE＝PF+EF＝2+．
∵H′M＝＝，
∴H′N＝H′M•sin30°＝，
∴此时点H′的横坐标为PE﹣H′N＝2＝2+；
Ⅲ．当FH′所在直线与DE垂直时，如图，

∵∠H′FG′＝90°，GF∥DE，
∴∠GFH′＝90°，
∴H，F，H′三点在一条直线上，则∠H′FD＝30°，
过点H′作H′L⊥DF，交FD的延长线于点L，
H′L＝H′F•sin30°＝2×＝，
∴此时点H′的横坐标为EF﹣H′L＝2＝．
综上，当△G′FH′的边与线段DE垂直时，点H′的横坐标为2+3或2+或．
27．（2023•大连）如图，在平面直角坐标系中，抛物线C1：y＝x2上有两点A、B，其中点A的横坐标为﹣2，点B的横坐标为1，抛物线C2：y＝﹣x2+bx+c过点A、B．过A作AC∥x轴交抛物线C1另一点为点C．以AC、AC长为边向上构造矩形ACDE．
（1）求抛物线C2的解析式；
（2）将矩形ACDE向左平移m个单位，向下平移n个单位得到矩形A′C′D′E′，点C的对应点C′落在抛物线C1上．
①求n关于m的函数关系式，并直接写出自变量m的取值范围；
②直线A′E′交抛物线C1于点P，交抛物线C2于点Q．当点E′为线段PQ的中点时，求m的值；
③抛物线C2与边E′D′、A′C′分别相交于点M、N，点M、N在抛物线C2的对称轴同侧，当MN＝时，求点C′的坐标．

【答案】（1）y＝﹣x2﹣2x+4．
（2）①n＝﹣m2+4m（0＜m＜4）．
②．
③或．
【解答】（1）根据题意，点A的横坐标为﹣2，点B的横坐标为1，代入抛物线C1：y＝x2，
∴当x＝﹣2时，y＝（﹣2）2＝4，则A（﹣2，4），
当x＝1时，y＝1，则B（1，1），
将点A（﹣2，4），B（1，1）代入抛物线C2：y＝﹣x2+bx+c，
∴，
解得，
∴抛物线C2的解析式为y＝﹣x2﹣2x+4．
（2）①∵AC∥x轴交抛物线另一点为C，
当y＝4时，x＝±2，
∴C（2，4），
∵矩形ACDE向左平移m个单位，向下平移n个单位得到矩形A′C′D′E′，点C的对应点C′落在抛物线C1上．
∴C′（2﹣m，4﹣n），（2﹣m）2＝4﹣n，
整理得n＝﹣m2+4m，
∵m＞0，n＞0，
∴0＜m＜4，
∴n＝﹣m2+4m（0＜m＜4）；
②如图，

∵A（﹣2，4），C（2，4），
∴AC＝4，
∵，
∴E（﹣2，6），
由①可得A′（﹣2﹣m，m2﹣4m+4），E′（﹣2﹣m，m2﹣4m+6），
∴P，Q的横坐标为﹣2﹣m，分别代入C1，C2，
∴P（﹣2﹣m，m2+4m+4），Q（﹣2﹣m，﹣m2﹣2m+4），
∴，
∴PQ的中点坐标为（﹣2﹣m，m+4），
∵点E′为线段PQ的中点，
∴m2﹣4m+6＝m+4，
解得m＝或m＝（大于4，舍去）．
③如图，连接MN，过点N作NG⊥E′D′于点G，

则NG＝2，
∵，
∴，
设N（a，﹣a2﹣2a+4），则M（a﹣，﹣a2﹣2a+6），
将M点代入y＝﹣x2﹣2x+4，
得，
解得a＝，
当a＝，，
∴，
将y＝代入y＝x2，
解得，
∴或．
28．（2023•营口）如图，抛物线y＝ax2+bx﹣1（a≠0）与x轴交于点A（1，0）和点B，与y轴交于点C，抛物线的对称轴交x轴于点D（3，0），过点B作直线l⊥x轴，过点D作DE⊥CD，交直线l于点E．
（1）求抛物线的解析式；
（2）如图，点P为第三象限内抛物线上的点，连接CE和BP交于点Q，当＝时，求点P的坐标；
（3）在（2）的条件下，连接AC，在直线BP上是否存在点F，使得∠DEF＝∠ACD+∠BED？若存在，请直接写出点F的坐标；若不存在，请说明理由．

【答案】（1）y＝﹣；
（2）P（﹣3，﹣）；
（3）F（，﹣）或（10，4）．
【解答】解：（1）由题意得：B（5，0），
设抛物线的解析式为：y＝a（x﹣1）（x﹣5），过点C（0，﹣1），
∴﹣1＝a•（﹣1）×（﹣5），
∴a＝﹣，
∴y＝﹣（x﹣1）（x﹣5）＝﹣；
（2）如图1，

∵直线l⊥x轴，DE⊥CD，
∴∠COD＝∠CDE＝∠EBD＝90°，
∴∠ODC+∠OCD＝90°，∠ODC+∠BDE＝90°，
∴∠OCD＝∠BDE，
∴△OCD∽△BDE，
∴，
∵OC＝1，OD＝3，BD＝OB﹣OD＝5﹣3＝2，
∴，
∴BE＝6，
∴B（5，﹣6），
设CE的解析式为：y＝kx+b，
∴，
∴，
∴y＝﹣x+1，
作PT⊥x轴，交直线CE于点T，设P（m，﹣），
∴T（m，﹣m﹣1），PT∥BE，
∴PT＝（﹣m﹣1）﹣（﹣）＝，△PQT∽△BQE，
∴，
∴，
∴m1＝﹣3，m2＝14（舍去），
当m＝﹣3时，y＝﹣×（﹣3﹣1）×（﹣3﹣5）＝﹣，
∴P（﹣3，﹣）；
（3）存在F点满足∠DEF＝∠ACD+∠BED，理由如下：
由（2）知：△OCD∽△BDE，
∴∠BED＝∠CDO，
∴∠ACD+∠BED＝∠ACD+∠CDO＝∠OAC，
∵OA＝OC＝1，∠AOC＝90°，
∴∠OAC＝45°，
∵∠DEF＝∠ACD+∠BED，
∴∠DEF＝45°，
如图2，

当点F在BP上时，
方法一：直线EF，交y轴于点G，作GH⊥CE于点H，
∵直线CE的解析式为：y＝﹣x﹣1，
∴∠ECF＝∠BEC＝45°，
∴∠DEF＝∠BEC，
∴∠FEQ＝∠BED，
∴tan∠FEQ＝tan∠BED＝，
∴，
∴设GH＝t，EH＝3t，
∴CH＝GH＝t，
∵C（0，﹣1），E（5，﹣6），
∴CE＝5，
∴t+3t＝5，
∴t＝，
∴CG＝GH＝＝，
∴OG＝1+＝，
∴G（0，﹣），
∴直线EG的解析式为：y＝﹣x﹣，
∵P（﹣3，﹣），B（5，0），
∴直线PB的解析式为：y＝﹣4，
由得，
，
∴F1（），
方法二：如图3，

作ER⊥y轴于点R，
∵∠DEF＝45°，∠BER＝90°，
∴∠REF+∠BED＝45°，
∵tan∠BED＝，
∴tan∠REF＝，
又E（5，﹣6），
∴直线EF的解析式为：y＝﹣x﹣，
后面步骤同上，
如图4，

当点F在PB的延长线上时，设EF交x轴于点W，
∵∠DEF＝45°，tan∠BED＝，
∴tan∠BEF＝＝，
∴BW＝BE＝3，
∴W（8，0），
∴直线EF的解析式为：y＝2x﹣16，
由2x﹣16＝得：x＝10，
当x＝10时，y＝2×10﹣16＝4，
∴F2（10，4），
综上所述：F（，﹣）或（10，4）．