2023年四川省各市中考数学试题真题汇编——函数(含答案)

这是一份2023年四川省各市中考数学试题真题汇编——函数(含答案)，共65页。试卷主要包含了，且1＜m＜2，有下列结论等内容，欢迎下载使用。
函数A（真题汇编）2023年四川省各市中考数学试题全解析版
一．选择题（共11小题）;
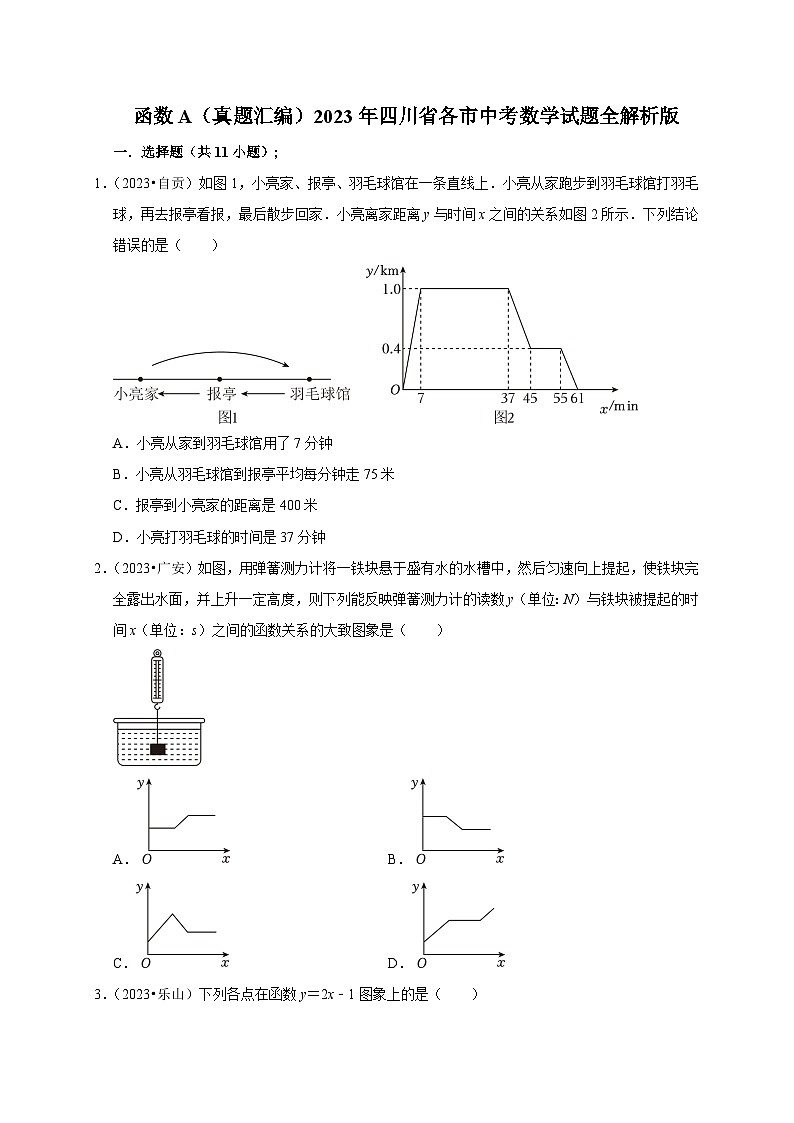
1．（2023•自贡）如图1，小亮家、报亭、羽毛球馆在一条直线上．小亮从家跑步到羽毛球馆打羽毛球，再去报亭看报，最后散步回家．小亮离家距离y与时间x之间的关系如图2所示．下列结论错误的是（　　）

A．小亮从家到羽毛球馆用了7分钟
B．小亮从羽毛球馆到报亭平均每分钟走75米
C．报亭到小亮家的距离是400米
D．小亮打羽毛球的时间是37分钟
2．（2023•广安）如图，用弹簧测力计将一铁块悬于盛有水的水槽中，然后匀速向上提起，使铁块完全露出水面，并上升一定高度，则下列能反映弹簧测力计的读数y（单位：N）与铁块被提起的时间x（单位：s）之间的函数关系的大致图象是（　　）

A． B．
C． D．
3．（2023•乐山）下列各点在函数y＝2x﹣1图象上的是（　　）
A．（﹣1，3） B．（0，1） C．（1，﹣1） D．（2，3）
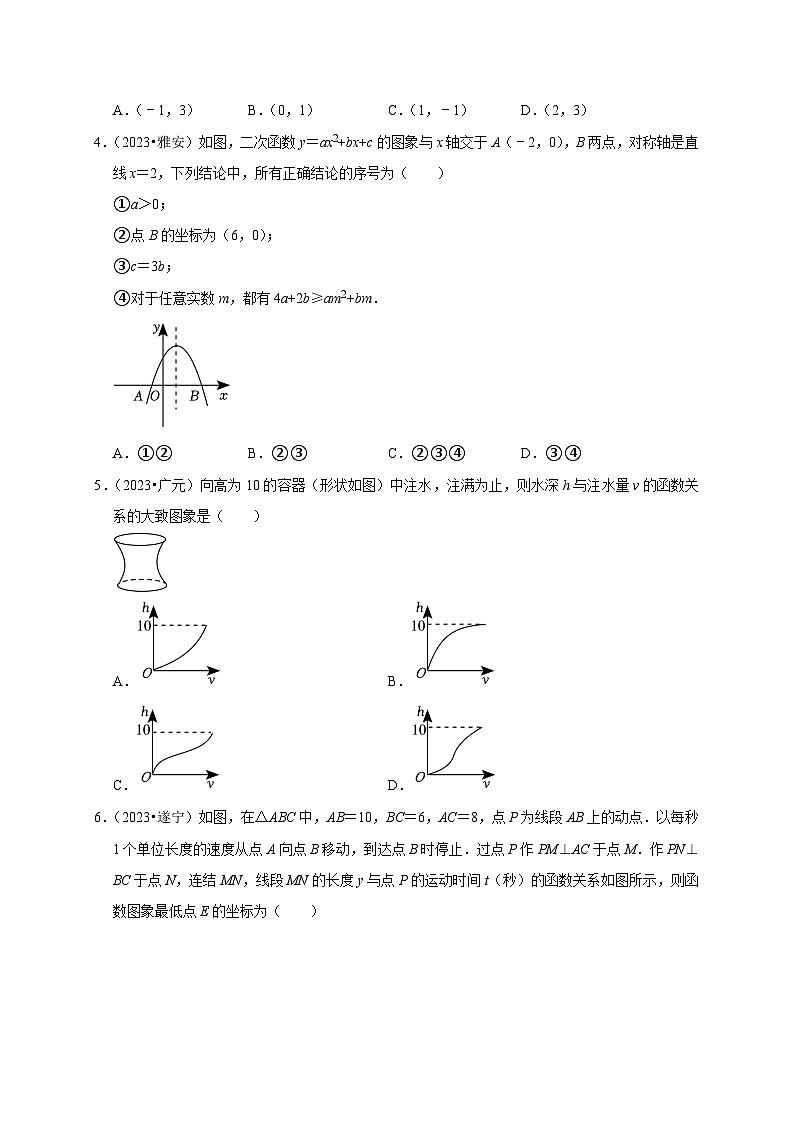
4．（2023•雅安）如图，二次函数y＝ax2+bx+c的图象与x轴交于A（﹣2，0），B两点，对称轴是直线x＝2，下列结论中，所有正确结论的序号为（　　）
①a＞0；
②点B的坐标为（6，0）；
③c＝3b；
④对于任意实数m，都有4a+2b≥am2+bm．

A．①② B．②③ C．②③④ D．③④
5．（2023•广元）向高为10的容器（形状如图）中注水，注满为止，则水深h与注水量v的函数关系的大致图象是（　　）

A． B．
C． D．
6．（2023•遂宁）如图，在△ABC中，AB＝10，BC＝6，AC＝8，点P为线段AB上的动点．以每秒1个单位长度的速度从点A向点B移动，到达点B时停止．过点P作PM⊥AC于点M．作PN⊥BC于点N，连结MN，线段MN的长度y与点P的运动时间t（秒）的函数关系如图所示，则函数图象最低点E的坐标为（　　）

A．（5，5） B．（6，） C．（，） D．（，5）
7．（2023•雅安）在平面直角坐标系中，将函数y＝x的图象绕坐标原点逆时针旋转90°，再向上平移1个单位长度，所得直线的函数表达式为（　　）
A．y＝﹣x+1 B．y＝x+1 C．y＝﹣x﹣1 D．y＝x﹣1
8．（2023•广元）已知抛物线y＝ax2+bx+c（a，b，c是常数且a＜0）过（﹣1，0）和（m，0）两点，且3＜m＜4，下列四个结论：
①abc＞0；
②3a+c＞0；
③若抛物线过点（1，4），则﹣1＜a＜；
④若关于x的方程a（x+1）（x﹣m）＝3有实数根，则4ac﹣b2≥12a，其中正确的结论有（　　）
A．1个 B．2个 C．3个 D．4个
9．（2023•乐山）如图，抛物线y＝ax2+bx+c经过点A（﹣1，0）、B（m，0），且1＜m＜2，有下列结论：
①b＜0；
②a+b＞0；
③0＜a＜﹣c；
④若点C（﹣，y1），D（，y2）在抛物线上，则y1＞y2．
其中，正确的结论有（　　）

A．4个 B．3个 C．2个 D．1个
10．（2023•巴中）在平面直角坐标系中，直线y＝kx+1与抛物线y＝x2交于A、B两点，设A（x1，y1），B（x2，y2），则下列结论正确的个数为（　　）
①x1•x2＝﹣4．
②y1+y2＝4k2+2．
③当线段AB长取最小值时，则△AOB的面积为2．
④若点N（0，﹣1），则AN⊥BN．

A．1 B．2 C．3 D．4
11．（2023•巴中）一次函数y＝（k﹣3）x+2的函数值y随x增大而减小，则k的取值范围是（　　）
A．k＞0 B．k＜0 C．k＞3 D．k＜3
二．填空题（共7小题）
12．（2023•巴中）已知a为正整数，点P（4，2﹣a）在第一象限中，则a＝　 　．
13．（2023•巴中）规定：如果两个函数的图象关于y轴对称，那么称这两个函数互为“Y函数”．例如：函数y＝x+3与y＝﹣x+3互为“Y函数”．若函数y＝x2+（k﹣1）x+k﹣3的图象与x轴只有一个交点，则它的“Y函数”图象与x轴的交点坐标为 　 　．
14．（2023•广安）函数y＝的自变量x的取值范围是 　 　．
15．（2023•成都）若点A（﹣3，y1），B（﹣1，y2）都在反比例函数y＝的图象上，则y1　 　y2（填“＞”或“＜”）．
16．（2023•内江）如图，在平面直角坐标系中，O为坐标原点，MN垂直于x轴，以MN为对称轴作△ODE的轴对称图形，对称轴MN与线段DE相交于点F，点D的对应点B恰好落在反比例函数y＝（x＜0）的图象上，点O、E的对应点分别是点C、A，若点A为OE的中点，且S△EAF＝，则k的值为 　 　．

17．（2023•乐山）定义：若x，y满足x2＝4y+t，y2＝4x+t且x≠y（t为常数），则称点M（x，y）为“和谐点”．
（1）若P（3，m）是“和谐点”，则m＝　 　；
（2）若双曲线y＝（﹣3＜x＜﹣1）存在“和谐点”，则k的取值范围 　 　．
18．（2023•宜宾）如图，抛物线y＝ax2+bx+c经过点A（﹣3，0），顶点为M（﹣1，m），且抛物线与y轴的交点B在（0，﹣2）与（0，﹣3）之间（不含端点），则下列结论：①当﹣3≤x≤1时，y≤0；②当△ABM的面积为时，a＝；③当△ABM为直角三角形时，在△AOB内存在唯一一点P，使得PA+PO+PB的值最小，最小值的平方为18+9．其中正确的结论是 　 　．（填写所有正确结论的序号）

三．解答题（共20小题）
19．（2023•雅安）李叔叔批发甲、乙两种蔬菜到菜市场去卖，已知甲、乙两种蔬菜的批发价和零售价如下表所示：
品名
甲蔬菜
乙蔬菜
批发价/（元/kg）
4.8
4
零售价/（元/kg）
7.21
5.6
（1）若他批发甲、乙两种蔬菜共40kg花180元，求批发甲、乙两种蔬菜各多少千克？（列方程或方程组求解）
（2）若他批发甲、乙两种蔬菜共80kg花m元，设批发甲种蔬菜nkg，求m与n的函数关系式；
（3）在（2）的条件下，全部卖完蔬菜后要保证利润不低于176元，至少批发甲种蔬菜多少千克？
20．（2023•内江）如图，在平面直角坐标系中，一次函数y＝mx+n与反比例函数的图象在第一象限内交于A（a，4）和B（4，2）两点，直线AB与x轴相交于点C，连接OA．
（1）求一次函数与反比例函数的表达式；
（2）当x＞0时，请结合函数图象，直接写出关于x的不等式mx+n的解集；
（3）过点B作BD平行于x轴，交OA于点D，求梯形OCBD的面积．

21．（2023•宜宾）如图，在平面直角坐标系xOy中，等腰直角三角形ABC的直角顶点C（3，0），顶点A、B（6，m）恰好落在反比例函数y＝第一象限的图象上．
（1）分别求反比例函数的表达式和直线AB所对应的一次函数的表达式；
（2）在x轴上是否存在一点P，使△ABP周长的值最小．若存在，求出最小值；若不存在，请说明理由．

22．（2023•达州）某县著名传统土特产品“豆笋”、“豆干”以“浓郁豆香，绿色健康”享誉全国，深受广大消费者喜爱．已知2件豆笋和3件豆干进货价为240元，3件豆笋和4件豆干进货价为340元．
（1）分别求出每件豆笋、豆干的进价；
（2）某特产店计划用不超过10440元购进豆笋、豆干共200件，且豆笋的数量不低于豆干数量的，该特产店有哪几种进货方案？
（3）若该特产店每件豆笋售价为80元，每件豆干售价为55元，在（2）的条件下，怎样进货可使该特产店获得利润最大，最大利润为多少元？
23．（2023•成都）2023年7月28日至8月8日，第31届世界大学生运动会将在成都举行．“当好东道主，热情迎嘉宾”，成都某知名小吃店计划购买A，B两种食材制作小吃．已知购买1千克A种食材和1千克B种食材共需68元，购买5千克A种食材和3千克B种食材共需280元．
（1）求A，B两种食材的单价；
（2）该小吃店计划购买两种食材共36千克，其中购买A种食材千克数不少于B种食材千克数的2倍，当A，B两种食材分别购买多少千克时，总费用最少？并求出最少总费用．
24．（2023•德阳）2022年8月27日至29日，以“新能源、新智造、新时代”为主题的世界清洁能源装备大会在德阳举行．大会聚焦清洁能源装备产业发展热点和前瞻性问题，着力实现会展聚集带动产业聚集，其中德阳清洁能源装备特色小镇位于德阳经济技术开发区，规划面积4.82平方公里，计划2025年基本建成，若甲、乙两个工程队计划参与修建“特色小镇”中的某项工程，已知由甲单独施工需要18个月完成任务，若由乙先单独施工2个月，再由甲、乙合作施工10个月恰好完成任务．承建公司每个月需要向甲工程队支付施工费用8万元，向乙工程队支付施工费用5万元．
（1）乙队单独施工需要几个月才能完成任务？
（2）为保证该工程在两年内完工，且尽可能的减少成本，承建公司决定让甲、乙两个工程队同时施工，并将该工程分成两部分，甲队完成其中一部分工程用了a个月，乙队完成另一部分工程用了b个月，已知甲队施工时间不超过6个月，乙队施工时间不超过24个月，且a，b为正整数，则甲乙两队实际施工的时间安排有几种方式？哪种安排方式所支付费用最低？
25．（2023•德阳）如图，点A在反比例函数y＝（k≠0）的图象上，点C是点A关于y轴的对称点，△OAC的面积是8．
（1）求反比例函数的解析式；
（2）当点A的横坐标为2时，过点C的直线y＝2x+b与反比例函数的图象相交于点P，求交点P的坐标．

26．（2023•雅安）如图，在平面直角坐标系中，四边形OABC是边长为2的正方形，点A，C在坐标轴上，反比例函数y＝（x＞0）的图象经过点B．
（1）求反比例函数的表达式；
（2）点D在反比例函数图象上，且横坐标大于2，S△OBD＝3，求直线BD的函数表达式．

27．（2023•广元）某移动公司推出A，B两种电话计费方式．
计费方式
月使用费/元
主叫限定时间/min
主叫超时费/（元/min）
被叫
A
78
200
0.25
免费
B
108
500
0.19
免费
（1）设一个月内用移动电话主叫时间为tmin，根据上表，分别写出在不同时间范围内，方式A，方式B的计费金额y1，y2关于t的函数解析式；
（2）若你预计每月主叫时间为350min，你将选择A，B哪种计费方式，并说明理由；
（3）请你根据月主叫时间t的不同范围，直接写出最省钱的计费方式．
28．（2023•广元）如图，已知一次函数y＝kx+6的图象与反比例函数y＝（m＞0）的图象交于A（3，4），B两点，与x轴交于点C，将直线AB沿y轴向上平移3个单位长度后与反比例函数图象交于点D，E．
​（1）求k，m的值及C点坐标；
（2）连接AD，CD，求△ACD的面积．

29．（2023•内江）某水果种植基地为响应政府号召，大力种植优质水果．某超市看好甲、乙两种优质水果的市场价值，经调查，这两种水果的进价和售价如表所示：
水果种类
进价（元/千克）
售价（元/千克）
甲
a
20
乙
b
23
该超市购进甲种水果15千克和乙种水果5千克需要305元；购进甲种水果20千克和乙种水果10千克需要470元．
（1）求a，b的值；
（2）该超市决定每天购进甲、乙两种水果共100千克进行销售，其中甲种水果的数量不少于30千克，且不大于80千克．实际销售时，若甲种水果超过60千克，则超过部分按每千克降价3元销售，求超市当天售完这两种水果获得的利润y（元）与购进甲种水果的数量x（千克）之间的函数关系式，并写出x的取值范围；
（3）在（2）的条件下，超市在获得的利润y（元）取得最大值时，决定售出的甲种水果每千克降价3m元，乙种水果每千克降价m元，若要保证利润率（利润率＝）不低于16%，求m的最大值．
30．（2023•乐山）如图，一次函数y＝kx+b的图象与反比例函数y＝的图象交于点A（m，4），与x轴交于点B，与y轴交于点C（0，3）．
（1）求m的值和一次函数的表达式；
（2）已知P为反比例函数y＝图象上的一点，S△OBP＝2S△OAC，求点P的坐标．
​

31．（2023•巴中）如图，正比例函数y＝kx（k≠0）与反比例函数y＝（m≠x）的图象交于A、B两点，A的横坐标为﹣4，B的纵坐标为﹣6．
（1）求反比例函数的表达式．
（2）观察图象，直接写出不等式kx＜的解集．
（3）将直线AB向上平移n个单位，交双曲线于C、D两点，交坐标轴于点E、F，连接OD、BD，若△OBD的面积为20，求直线CD的表达式．

32．（2023•泸州）如图，在平面直角坐标系xOy中，直线l：y＝kx+2与x，y轴分别相交于点A，B，与反比例函数y＝（x＞0）的图象相交于点C，已知OA＝1，点C的横坐标为2．
（1）求k，m的值；
（2）平行于y轴的动直线与l和反比例函数的图象分别交于点D，E，若以B，D，E，O为顶点的四边形为平行四边形，求点D的坐标．

33．（2023•德阳）已知：在平面直角坐标系中，抛物线与x轴交于点A（﹣4，0），B（2，0），与y轴交于点C（0，﹣4）．
（1）求抛物线的解析式；
（2）如图1，如果把抛物线x轴下方的部分沿x轴翻折180°，抛物线的其余部分保持不变，得到一个新图象．当平面内的直线y＝kx+6与新图象有三个公共点时，求k的值；
（3）如图2，如果把直线AB沿y轴向上平移至经过点D，与抛物线的交点分别是E，F，直线BC交EF于点H，过点F作FG⊥CH于点G，若，求点F的坐标．
​
34．（2023•雅安）在平面直角坐标系中，已知抛物线y＝x2+bx+c过点A（0，2），对称轴是直线x＝2．
（1）求此抛物线的函数表达式及顶点M的坐标；
（2）若点B在抛物线上，过点B作x轴的平行线交抛物线于点C，当△BCM是等边三角形时，求出此三角形的边长；
（3）已知点E在抛物线的对称轴上，点D的坐标为（1，﹣1）是否存在点F，使以点A，D，E，F为顶点的四边形为菱形？若存在，请直接写出点F的坐标；若不存在，请说明理由．

35．（2023•巴中）在平面直角坐标系中，抛物线y＝ax2+bx+c（a≠0）经过点A（﹣1，0）和B（0，3），其顶点的横坐标为1．
（1）求抛物线的表达式．
（2）若直线x＝m与x轴交于点N，在第一象限内与抛物线交于点M，当m取何值时，使得AN+MN有最大值，并求出最大值．
（3）若点P为抛物线y＝ax2+bx+c（a≠0）的对称轴上一动点，将抛物线向左平移1个单位长度后，Q为平移后抛物线上一动点．在（2）的条件下求得的点M，是否能与A、P、Q构成平行四边形？若能构成，求出Q点坐标；若不能构成，请说明理由．

36．（2023•广元）如图1，在平面直角坐标系中，已知二次函数y＝ax2+bx+4的图象与x轴交于点A（﹣2，0），B（4，0），与y轴交于点C．
（1）求抛物线的解析式；
（2）已知E为抛物线上一点，F为抛物线对称轴l上一点，以B，E，F为顶点的三角形是等腰直角三角形，且∠BFE＝90°，求出点F的坐标；
（3）如图2，P为第一象限内抛物线上一点，连接AP交y轴于点M，连接BP并延长交y轴于点N，在点P运动过程中，OM+ON是否为定值？若是，求出这个定值；若不是，请说明理由．

37．（2023•乐山）已知（x1，y1），（x2，y2）是抛物线C1：y＝﹣x2+bx（b为常数）上的两点，当x1+x2＝0时，总有y1＝y2．
（1）求b的值；
（2）将抛物线C1平移后得到抛物线C2：y＝﹣（x﹣m）2+1（m＞0）．
当0≤x≤2时，探究下列问题：
①若抛物线C1与抛物线C2有一个交点，求m的取值范围；
②设抛物线C2与x轴交于A，B两点，与y轴交于点C，抛物线C2的顶点为点E，△ABC外接圆的圆心为点F．如果对抛物线C1上的任意一点P，在抛物线C2上总存在一点Q，使得点P、Q的纵坐标相等．求EF长的取值范围．
38．（2023•内江）如图，在平面直角坐标系中，抛物线y＝ax2+bx+c与x轴交于B（4，0），C（﹣2，0）两点，与y轴交于点A（0，﹣2）．
（1）求该抛物线的函数表达式；
（2）若点P是直线AB下方抛物线上的一动点，过点P作x轴的平行线交AB于点K，过点P作y轴的平行线交x轴于点D，求的最大值及此时点P的坐标；
（3）在抛物线的对称轴上是否存在一点M，使得△MAB是以AB为一条直角边的直角三角形；若存在，请求出点M的坐标，若不存在，请说明理由．


函数A（真题汇编）2023年四川省各市中考数学试题全解析版
参考答案与试题解析
一．选择题（共11小题）
1．（2023•自贡）如图1，小亮家、报亭、羽毛球馆在一条直线上．小亮从家跑步到羽毛球馆打羽毛球，再去报亭看报，最后散步回家．小亮离家距离y与时间x之间的关系如图2所示．下列结论错误的是（　　）

A．小亮从家到羽毛球馆用了7分钟
B．小亮从羽毛球馆到报亭平均每分钟走75米
C．报亭到小亮家的距离是400米
D．小亮打羽毛球的时间是37分钟
【答案】D
【解答】解：A、由图象得：小亮从家到羽毛球馆用了7分钟，故A选项不符合题意；
B、由图象可知：小亮从羽毛球馆到报亭的平均速度为：（1.0﹣0.4）÷（45﹣37）＝0.075（千米/分）＝75（米/分），故B选项不符合题意；
C、由图象知报亭到小亮家的距离是0.4千米，即400米，故C选项不符合题意；
D、由图象知小亮打羽毛球的时间是37﹣7＝30（分钟），故D选项符合题意；
故选：D．
2．（2023•广安）如图，用弹簧测力计将一铁块悬于盛有水的水槽中，然后匀速向上提起，使铁块完全露出水面，并上升一定高度，则下列能反映弹簧测力计的读数y（单位：N）与铁块被提起的时间x（单位：s）之间的函数关系的大致图象是（　　）

A． B．
C． D．
【答案】A
【解答】解：根据浮力的知识可知，当铁块露出水面之前，F拉+F浮＝G，
此过程浮力不变，铁块的重力不变，故拉力不变，即弹簧测力计的读数不变；
当铁块逐渐露出水面的过程中，F拉+F浮＝G，
此过程浮力逐渐减小，铁块重力不变，故拉力逐渐增大，即弹簧测力计的读数逐渐增大；
当铁块完全露出水面之后，F拉＝G，
此过程拉力等于铁块重力，即弹簧测力计的读数不变．
综上，弹簧测力计的读数先不变，再逐渐增大，最后不变．
故选：A．
3．（2023•乐山）下列各点在函数y＝2x﹣1图象上的是（　　）
A．（﹣1，3） B．（0，1） C．（1，﹣1） D．（2，3）
【答案】D
【解答】解：A．当x＝﹣1时，y＝2×（﹣1）﹣1＝﹣3，
∴点（﹣1，3）不在函数y＝2x﹣1图象上；
B．当x＝0时，y＝2×0﹣1＝﹣1，
∴点（0，1）不在函数y＝2x﹣1图象上；
C．当x＝1时，y＝2×1﹣1＝1，
∴点（1，﹣1）不在函数y＝2x﹣1图象上；
D．当x＝2时，y＝2×2﹣1＝3，
∴点（2，3）在函数y＝2x﹣1图象上；
故选：D．
4．（2023•雅安）如图，二次函数y＝ax2+bx+c的图象与x轴交于A（﹣2，0），B两点，对称轴是直线x＝2，下列结论中，所有正确结论的序号为（　　）
①a＞0；
②点B的坐标为（6，0）；
③c＝3b；
④对于任意实数m，都有4a+2b≥am2+bm．

A．①② B．②③ C．②③④ D．③④
【答案】C
【解答】解：∵抛物线开口向下，
∴a＜0，①错误，
∵A、B关于对称轴x＝2对称，
∴B点的横坐标为6，②正确，
∵二次函数y＝ax2+bx+c的对称轴为直线x＝2，
∴﹣＝2，
∴，
把（﹣2，0）代入y＝ax2+bx+c，得：
4a﹣2b+c＝0，
∴﹣2b+c＝0，整理得：
c＝3b，③正确，
∵二次函数y＝ax2+bx+c的对称轴为直线x＝2，
∴当x＝2时，抛物线取得最大值为y＝4a+2b+c，
当x＝m时，y＝am2+bm+c，
∴4a+2b+c≥am2+bm+c，
即a+b≥am2+bmm，④正确．
∴所有正确结论的序号为②③④．
故选：C．
5．（2023•广元）向高为10的容器（形状如图）中注水，注满为止，则水深h与注水量v的函数关系的大致图象是（　　）

A． B．
C． D．
【答案】D
【解答】解：依据题意，从水瓶的构造形状上看，从底部到顶部的变化关系为：开始宽，逐渐细小，再变宽．
则注入的水量V随水深h的变化关系为：先慢再快，最后又变慢．
那么从函数的图象上看，
C对应的图象变化为先快再慢，最后又变快，不符合．
A、B对应的图象中间没有变化，只有D符合条件．
故选：D．
6．（2023•遂宁）如图，在△ABC中，AB＝10，BC＝6，AC＝8，点P为线段AB上的动点．以每秒1个单位长度的速度从点A向点B移动，到达点B时停止．过点P作PM⊥AC于点M．作PN⊥BC于点N，连结MN，线段MN的长度y与点P的运动时间t（秒）的函数关系如图所示，则函数图象最低点E的坐标为（　　）

A．（5，5） B．（6，） C．（，） D．（，5）
【答案】C
【解答】解：连接CP，
∵AB＝10，BC＝6，AC＝8，
∴AC2+BC2＝82+62＝102＝AB2，
∴△ABC是直角三角形，∠ACB＝90°，
∵PM⊥AC，PN⊥BC，
∴∠PMC＝∠PNC＝90°，
∴∠PMC＝∠PNC＝∠ACB＝90°，
∴四边形CMPN是矩形，
∴MN＝CP，
当CP⊥AB时，CP取得最小值，此时CP＝＝＝，AP＝＝＝，
∴函数图象最低点E的坐标为（，），
故选：C．

7．（2023•雅安）在平面直角坐标系中，将函数y＝x的图象绕坐标原点逆时针旋转90°，再向上平移1个单位长度，所得直线的函数表达式为（　　）
A．y＝﹣x+1 B．y＝x+1 C．y＝﹣x﹣1 D．y＝x﹣1
【答案】A
【解答】解：在函数y＝x的图象上取点A（1，1），
绕原点逆时针方向旋转90°后得到对应的点的坐标A′（﹣1，1），
则旋转后的直线的解析式为y＝﹣x，
再向上平移1个单位长度，得到y＝﹣x+1．
故选：A．
8．（2023•广元）已知抛物线y＝ax2+bx+c（a，b，c是常数且a＜0）过（﹣1，0）和（m，0）两点，且3＜m＜4，下列四个结论：
①abc＞0；
②3a+c＞0；
③若抛物线过点（1，4），则﹣1＜a＜；
④若关于x的方程a（x+1）（x﹣m）＝3有实数根，则4ac﹣b2≥12a，其中正确的结论有（　　）
A．1个 B．2个 C．3个 D．4个
【答案】B
【解答】解：∵抛物线y＝ax2+bx+c（a，b，c是常数），过A（﹣1，0），B（m，0）两点，且3＜m＜4，
∴对称轴x＝＞1，
∴对称轴在y轴右侧，
∴﹣＞0，
∵a＜0，
∴b＞0，c＞0，
∴abc＜0，
故①错误；
∵﹣＞1，a＜0，
∴﹣b＜2a，
∵抛物线y＝ax2+bx+c（a，b，c是常数），过A（﹣1，0），
∴a﹣b+c＝0，
∴3a+c＞0，
故②正确；
∵抛物线y＝ax2+bx+c（a，b，c是常数），过A（﹣1，0），点（1，4），
∴，
解得，
∵抛物线y＝ax2+2x+2﹣a，
∵抛物线y＝ax2+bx+c（a，b，c是常数且a＜0）过（﹣1，0）和（m，0）两点，
∴y＝a（x+1）（x﹣m）＝ax2+a（1﹣m）x﹣am，
∴﹣am＝2﹣a，
∴m＝＝1﹣，
∵3＜m＜4，
∴3＜1﹣＜4，
∵a＜0，
∴﹣1＜a＜，
故③正确；
∵若关于x的方程a（x+1）（x﹣m）＝3有实数根，
∴抛物线y＝ax2+bx+c（a，b，c是常数且a＜0）与直线y＝3有交点，
∴，
∴4ac﹣b2≤12a，
故④错误．
故选：B．
9．（2023•乐山）如图，抛物线y＝ax2+bx+c经过点A（﹣1，0）、B（m，0），且1＜m＜2，有下列结论：
①b＜0；
②a+b＞0；
③0＜a＜﹣c；
④若点C（﹣，y1），D（，y2）在抛物线上，则y1＞y2．
其中，正确的结论有（　　）

A．4个 B．3个 C．2个 D．1个
【答案】B
【解答】解：∵抛物线开口向上，
∴a＞0，
∵抛物线的对称轴在y轴的右侧，
∴b＜0，故①正确；
∵抛物线与y轴的交点在x轴下方，
∴c＜0，
∵抛物线经过点A（﹣1，0），
∴a﹣b+c＝0，
∴c＝b﹣a，
∵当x＝2时，y＞0，
∴4a+2b+c＞0，
∴4a+2b+b﹣a＞0，
∴3a+3b＞0，
∴a+b＞0，故②正确；
∵a﹣b+c＝0，
∴a+c＝b，
∵b＜0，
∴a+c＜0，
∴0＜a＜﹣c，故③正确；
∵点C（﹣，y1）到对称轴的距离比点D（，y2）到对称轴的距离近，
∴y1＜y2，故④的结论错误．
故选：B．
10．（2023•巴中）在平面直角坐标系中，直线y＝kx+1与抛物线y＝x2交于A、B两点，设A（x1，y1），B（x2，y2），则下列结论正确的个数为（　　）
①x1•x2＝﹣4．
②y1+y2＝4k2+2．
③当线段AB长取最小值时，则△AOB的面积为2．
④若点N（0，﹣1），则AN⊥BN．

A．1 B．2 C．3 D．4
【答案】C
【解答】解：由题意，联列方程组
∴可得得x1，x2满足方程x2﹣kx﹣1＝0；y1，y2满足方程y2﹣（2+4k2）y+1＝0．
依据根与系数的关系得，x1+x2＝4k，x1•x2＝﹣4，y1+y2＝4k2+2，y1•y2＝1，
∴①、②正确．
由两点间距离公式得，AB＝＝＝4（k2+1）．
∴当k＝0时，AB最小值为4．
∴S△AOB＝×1×AB＝2．
∴③正确．
由题意，kAN＝，kBN＝，
∴kAN•kBN＝•＝＝＝﹣k2﹣1．
∴当k＝0时，AN⊥BN；当k≠0是，AN与BN不垂直．
∴④错误．
故选：C．
11．（2023•巴中）一次函数y＝（k﹣3）x+2的函数值y随x增大而减小，则k的取值范围是（　　）
A．k＞0 B．k＜0 C．k＞3 D．k＜3
【答案】D
【解答】解：∵一次函数y＝（k﹣3）x+2的函数值y随x增大而减小，
∴k﹣3＜0，
∴k＜3，
故选：D．
二．填空题（共7小题）
12．（2023•巴中）已知a为正整数，点P（4，2﹣a）在第一象限中，则a＝　1　．
【答案】见试题解答内容
【解答】解：∵点P（4，2﹣a）在第一象限，
∴2﹣a＞0，
∴a＜2，
又a为正整数，
∴a＝1．
故答案为：1．
13．（2023•巴中）规定：如果两个函数的图象关于y轴对称，那么称这两个函数互为“Y函数”．例如：函数y＝x+3与y＝﹣x+3互为“Y函数”．若函数y＝x2+（k﹣1）x+k﹣3的图象与x轴只有一个交点，则它的“Y函数”图象与x轴的交点坐标为 　（3，0）或（4，0）　．
【答案】（3，0）或（4，0）．
【解答】解：当k＝0时，函数解析式为y＝﹣x﹣3，
它的“Y函数”解析式为y＝x﹣3，它们的图象与x轴都只有一个交点，
∴它的“Y函数”图象与x轴的交点坐标为（3，0）；
当k≠0时，此函数为二次函数，
若二次函数的图象与x轴只有一个交点，
则二次函数的顶点在x轴上，
即，
解得k＝﹣1，
∴二次函数的解析式为＝，
∴它的“Y函数”解析式为，
令y＝0，
则，
解得x＝4，
∴二次函数的“Y函数”图象与x轴的交点坐标为（4，0），
综上，它的“Y函数”图象与x轴的交点坐标为（3，0）或（4，0）．
故答案为：（3，0）或（4，0）．
14．（2023•广安）函数y＝的自变量x的取值范围是 　x≥﹣2且x≠1　．
【答案】见试题解答内容
【解答】解：根据题意得：，
解得：x≥﹣2且x≠1．
故答案为：x≥﹣2且x≠1．
15．（2023•成都）若点A（﹣3，y1），B（﹣1，y2）都在反比例函数y＝的图象上，则y1　＞　y2（填“＞”或“＜”）．
【答案】＞．
【解答】解：∵y＝中k＝6＞0，
∴在每个象限内，y随x的增大而减小，
∵﹣3＜﹣1＜0，
∴y1＞y2．
故答案为：＞．
16．（2023•内江）如图，在平面直角坐标系中，O为坐标原点，MN垂直于x轴，以MN为对称轴作△ODE的轴对称图形，对称轴MN与线段DE相交于点F，点D的对应点B恰好落在反比例函数y＝（x＜0）的图象上，点O、E的对应点分别是点C、A，若点A为OE的中点，且S△EAF＝，则k的值为 　﹣6　．

【答案】﹣6．
【解答】解：连接OB，设对称轴MN与x轴交于G，
∵△ODE与△CBA关于MN对称，
∴AG＝EG，AC＝EO，EC＝AO，
∵点A我OE的中点，
设AG＝EG＝a，则EC＝AO＝AE＝2a，
∴AC＝EO＝4a，
∵S△EAF＝，
∴S△EGF＝，
∵GF∥OD，
∴△EFG∽△EDO，
∴，
即，
∴，
∴S△ACB＝2，
∵AC＝4a，AO＝2a，
∴S△OCB＝S△ACB+S△AOB＝2+1＝3，
∴|k|＝3，
∵k＜0，
∴k＝﹣6，
故答案为：﹣6．

17．（2023•乐山）定义：若x，y满足x2＝4y+t，y2＝4x+t且x≠y（t为常数），则称点M（x，y）为“和谐点”．
（1）若P（3，m）是“和谐点”，则m＝　﹣7　；
（2）若双曲线y＝（﹣3＜x＜﹣1）存在“和谐点”，则k的取值范围 　3＜k＜4　．
【答案】（1）﹣7；
（2）3＜k＜4．
【解答】解：（1）∵P（3，m）是“和谐点”，
∴，
消去t得到m2+4m﹣21＝0，
解得m＝﹣7或3，
∵x≠y，
∴m＝﹣7；
故答案为：﹣7；
（2）∵双曲线y＝（﹣3＜x＜﹣1）存在“和谐点”，
∴，
①﹣②得（x+）（x﹣）＝﹣4（x﹣），
∴（x﹣）（x++4）＝0，
∵x≠y，
∴x++4＝0，
整理得k＝﹣x2﹣4x＝﹣（x+2）2+4，
∵﹣3＜x＜﹣1，
∴3＜k＜4．
故答案为：3＜k＜4．
18．（2023•宜宾）如图，抛物线y＝ax2+bx+c经过点A（﹣3，0），顶点为M（﹣1，m），且抛物线与y轴的交点B在（0，﹣2）与（0，﹣3）之间（不含端点），则下列结论：①当﹣3≤x≤1时，y≤0；②当△ABM的面积为时，a＝；③当△ABM为直角三角形时，在△AOB内存在唯一一点P，使得PA+PO+PB的值最小，最小值的平方为18+9．其中正确的结论是 　①②　．（填写所有正确结论的序号）

【答案】①②．
【解答】解：①∵抛物线y＝ax2+bx+c经过点A（﹣3，0），顶点为M（﹣1，m），
∴抛物线的对称轴为直线x＝﹣1，
∴抛物线与x轴的另一个交点坐标为（1，0），
∵抛物线的开口向上，
∴当﹣3≤x≤1时，y≤0；故①正确．
②将（﹣3，0），（1，0）代入y＝ax2+bx+c，得，
解得：，
∴y＝ax2+2ax﹣3a＝a（x+1）2﹣4a，
∴抛物线的顶点为M（﹣1，﹣4a），
设抛物线对称轴交x轴于H，如图，

则H（﹣1，0），
∴AH＝﹣1﹣（﹣3）＝2，MH＝4a，OH＝1，
∵B（0，﹣3a），
∴OB＝3a，
∴S△ABM＝S△AMH+S梯形BMHO﹣S△AOB＝•AH•MH+•（MH+OB）•OH﹣OA•OB＝×2×4a+×（4a+3a）×1﹣×3×3a＝3a，
∵S△ABM＝，
∴3a＝，
∴a＝；故②正确．
③∵A（﹣3，0），B（0，﹣3a），M（﹣1，﹣4a），
∴AB2＝OA2+OB2＝32+（3a）2＝9+9a2，AM2＝AH2+MH2＝4+16a2，BM2＝1+a2，
若∠AMB＝90°，则AM2+BM2＝AB2，
即4+16a2+1+a2＝9+9a2，
解得：a＝，或a＝﹣（舍去）；
若∠ABM＝90°，则AB2+BM2＝AM2，
即9+9a2+1+a2＝4+16a2，
解得：a＝1，或a＝﹣1（舍去）；
若∠BAM＝90°，则AB2+AM2＝BM2，
即9+9a2+4+16a2＝1+a2，
整理得：a2＝﹣（无解）；
∵点B在（0，﹣2）与（0，﹣3）之间（不含端点），
∴﹣3＜﹣3a＜﹣2，
∴＜a＜1，
∴a＝，
∴OB＝，AB2＝，
如图，将△BPA绕点B逆时针旋转60°得到△BP′A′，连接PP′，过点A′作A′T⊥x轴于点T，作A′Q⊥y轴于点Q，

∴BP＝BP′，PA＝P′A′，∠PBP′＝∠ABA′＝60°，
∴△BPP′和△ABA′是等边三角形，
∴BP＝PP′，AA′＝A′B＝AB＝，
∴PA+PO+PB＝P′A′+PO+PP′，
∴当点O，点P，点P′，点A′共线时，PA+PO+PB值最小，最小值为OA′，
此时∠APB＝∠APO＝∠BPO＝120°，
设A′（m，n），
则A′T＝﹣n，AT＝﹣3﹣m，A′Q＝﹣m，BQ＝﹣n﹣，
在Rt△AA′T中，AT2+A′T2＝AA′2，
在Rt△BA′Q中，BQ2+A′Q2＝A′B2，
即，
解得：，
∴OA′2＝m2+n2＝（）2+（）2＝，
故③错误；
故答案为：①②．
三．解答题（共20小题）
19．（2023•雅安）李叔叔批发甲、乙两种蔬菜到菜市场去卖，已知甲、乙两种蔬菜的批发价和零售价如下表所示：
品名
甲蔬菜
乙蔬菜
批发价/（元/kg）
4.8
4
零售价/（元/kg）
7.21
5.6
（1）若他批发甲、乙两种蔬菜共40kg花180元，求批发甲、乙两种蔬菜各多少千克？（列方程或方程组求解）
（2）若他批发甲、乙两种蔬菜共80kg花m元，设批发甲种蔬菜nkg，求m与n的函数关系式；
（3）在（2）的条件下，全部卖完蔬菜后要保证利润不低于176元，至少批发甲种蔬菜多少千克？
【答案】（1）批发甲种蔬菜25千克，批发乙种蔬菜15千克；
（2）m＝0.8n+320；
（3）至少批发甲种蔬菜千克．
【解答】解：（1）设批发甲种蔬菜x千克，批发乙种蔬菜y千克，根据题意得，
，解得，
答：批发甲种蔬菜25千克，批发乙种蔬菜15千克；
（2）根据题意得m＝4.8n+（80﹣n）×4，
整理得m＝0.8n+320；
（3）设全部卖完蔬菜后利润为w元，根据题意得，
w＝（7.21﹣4.8）n+（5.6﹣4）（80﹣n），
整理得w＝0.81n+128，
∵要保证利润不低于176元，
∴w＝0.81n+128≥176，
解得n≥，
∴至少批发甲种蔬菜千克．
20．（2023•内江）如图，在平面直角坐标系中，一次函数y＝mx+n与反比例函数的图象在第一象限内交于A（a，4）和B（4，2）两点，直线AB与x轴相交于点C，连接OA．
（1）求一次函数与反比例函数的表达式；
（2）当x＞0时，请结合函数图象，直接写出关于x的不等式mx+n的解集；
（3）过点B作BD平行于x轴，交OA于点D，求梯形OCBD的面积．

【答案】（1）反比例函数为，一次函数为y＝﹣x+6；
（2）2≤x≤4；
（3）9．
【解答】解：（1）∵反比例函数 过B（4，2），
∴k＝4×2＝8，
∴反比例函数为：，
把A（a，4）代入 得：，
∴A（2，4），
∴，
解得：，
∴一次函数为y＝﹣x+6；
（2）观察函数图象可得，当x＞0时，﹣x+6≥的解集为：2≤x≤4；
（3）∵A（2，4），
∴直线OA的解析式为：y＝2x，
∵过点B（4，2）作BD平行于x轴，交OA于点D，
∴D（1，2），
∴BD＝4﹣1＝3，
在y＝﹣x+6中，令y＝0得x＝6，即
∴C（6，0），
∴OC＝6，
∵，
∴梯形OCBD的面积为9．
21．（2023•宜宾）如图，在平面直角坐标系xOy中，等腰直角三角形ABC的直角顶点C（3，0），顶点A、B（6，m）恰好落在反比例函数y＝第一象限的图象上．
（1）分别求反比例函数的表达式和直线AB所对应的一次函数的表达式；
（2）在x轴上是否存在一点P，使△ABP周长的值最小．若存在，求出最小值；若不存在，请说明理由．

【答案】（1）反比例函数的表达式为y＝，直线AB所对应的一次函数的表达式为y＝﹣x+4；
（2）在x轴上存在一点P，使△ABP周长的值最小，周长的最小值为4+2．
【解答】解：（1）过A作AT⊥x轴于T，过B作BK⊥x轴于K，如图：

∵△ABC是等腰直角三角形，
∴AC＝BC，∠ACB＝90°，
∴∠ACT＝90°﹣∠BCK＝∠CBK，
∵∠ATC＝90°＝∠CKB，
∴△ATC≌△CKB（AAS），
∴AT＝CK，CT＝BK，
∵C（3，0），B（6，m），
∴AT＝CK＝6﹣3＝3，CT＝BK＝m，
∴OT＝3﹣m，
∴A（3﹣m，3），
∵A（3﹣m，3），B（6，m）恰好落在反比例函数y＝第一象限的图象上，
∴k＝3（3﹣m）＝6m，
∴m＝1，k＝6，
∴反比例函数的表达式为y＝，A（2，3），B（6，1），
设直线AB所对应的一次函数的表达式为y＝k'x+b，把A（2，3），B（6，1）代入得：
，
解得，
∴直线AB所对应的一次函数的表达式为y＝﹣x+4；
（2）在x轴上存在一点P，使△ABP周长的值最小，理由如下：
作A（2，3）关于x轴的对称点A'（2，﹣3），连接A'B交x轴于P，如图：

∵A（2，3），B（6，1），
∴AB＝＝2，
∴当AP+BP最小时，△ABP周长最小，
∵A，A'关于x轴对称，
∴AP＝A'P，
∴当A'，P，B共线时，AP+BP最小，△ABP周长也最小，
∵A'（2，﹣3），B（6，1），
∴A'B＝＝4，
∴AP+BP＝A'P+BP＝A'B＝4，
∴△ABP周长的最小值为4+2．
22．（2023•达州）某县著名传统土特产品“豆笋”、“豆干”以“浓郁豆香，绿色健康”享誉全国，深受广大消费者喜爱．已知2件豆笋和3件豆干进货价为240元，3件豆笋和4件豆干进货价为340元．
（1）分别求出每件豆笋、豆干的进价；
（2）某特产店计划用不超过10440元购进豆笋、豆干共200件，且豆笋的数量不低于豆干数量的，该特产店有哪几种进货方案？
（3）若该特产店每件豆笋售价为80元，每件豆干售价为55元，在（2）的条件下，怎样进货可使该特产店获得利润最大，最大利润为多少元？
【答案】（1）每件豆笋的进价为60元，每件豆干的进价为40元；
（2）该特产店有三种进货方案：购进豆笋120件，购进豆干80件；购进豆笋121件，购进豆干79件；购进豆笋122件，购进豆干78件；
（3）购进豆笋122件，购进豆干78件可使该特产店获得利润最大，最大利润为3610元．
【解答】解：（1）设每件豆笋的进价为x元，每件豆干的进价为y元，
由题意得：，
解得：，
∴每件豆笋的进价为60元，每件豆干的进价为40元；
（2）设购进豆笋a件，则购进豆干（200﹣a）件，
由题意可得：，
解得：120≤a≤122，且a为整数，
∴该特产店有以下三种进货方案：
当a＝120时，200﹣a＝80，即购进豆笋120件，购进豆干80件，
当a＝121时，200﹣a＝79，即购进豆笋121件，购进豆干79件，
当a＝122时，200﹣a＝78，即购进豆笋122件，购进豆干78件，
（3）设总利润为w元，
则w＝（80﹣60）•a+（55﹣40）•（200﹣a）＝5a+3000，
∵5＞0，
∴w随a的增大而增大，
∴当a＝122时，w取得最大值，最大值为5×122+3000＝3610，
∴购进豆笋122件，购进豆干78件可使该特产店获得利润最大，最大利润为3610元．
23．（2023•成都）2023年7月28日至8月8日，第31届世界大学生运动会将在成都举行．“当好东道主，热情迎嘉宾”，成都某知名小吃店计划购买A，B两种食材制作小吃．已知购买1千克A种食材和1千克B种食材共需68元，购买5千克A种食材和3千克B种食材共需280元．
（1）求A，B两种食材的单价；
（2）该小吃店计划购买两种食材共36千克，其中购买A种食材千克数不少于B种食材千克数的2倍，当A，B两种食材分别购买多少千克时，总费用最少？并求出最少总费用．
【答案】（1）A种食材单价是每千克38元，B种食材单价是每千克30元；
（2）A种食材购买24千克，B种食材购买12千克时，总费用最少，为1272元．
【解答】（1）设A种食材的单价为x元/千克，B种食材的单价为y元/千克，由题意得：
，
解得：，
∴A种食材单价是每千克38元，B种食材单价是每千克30元；
（2）设A种食材购买m千克，B种食材购买（36﹣m）千克，总费用为w元，由题意得：
w＝38m+30（36﹣m）＝8m+1080，
∵m≥2（36﹣m），
∴24≤m＜36，
∵k＝8＞0，
∴w随m的增大而增大，
∴当m＝24时，w有最小值为：8×24+1080＝1272（元），
∴A种食材购买24千克，B种食材购买12千克时，总费用最少，为1272元．
24．（2023•德阳）2022年8月27日至29日，以“新能源、新智造、新时代”为主题的世界清洁能源装备大会在德阳举行．大会聚焦清洁能源装备产业发展热点和前瞻性问题，着力实现会展聚集带动产业聚集，其中德阳清洁能源装备特色小镇位于德阳经济技术开发区，规划面积4.82平方公里，计划2025年基本建成，若甲、乙两个工程队计划参与修建“特色小镇”中的某项工程，已知由甲单独施工需要18个月完成任务，若由乙先单独施工2个月，再由甲、乙合作施工10个月恰好完成任务．承建公司每个月需要向甲工程队支付施工费用8万元，向乙工程队支付施工费用5万元．
（1）乙队单独施工需要几个月才能完成任务？
（2）为保证该工程在两年内完工，且尽可能的减少成本，承建公司决定让甲、乙两个工程队同时施工，并将该工程分成两部分，甲队完成其中一部分工程用了a个月，乙队完成另一部分工程用了b个月，已知甲队施工时间不超过6个月，乙队施工时间不超过24个月，且a，b为正整数，则甲乙两队实际施工的时间安排有几种方式？哪种安排方式所支付费用最低？
【答案】（1）乙队单独施工需要27个月才能完成任务；
（2）有三种方式，方案一：甲队施工2个月，乙队施工24个月；方案二：甲队施工4个月，乙队施工21个月；方案三：甲队施工6个月，乙队施工18个月．方案一所支付费用最低．
【解答】解：（1）设乙队单独施工需要x个月才能完成任务，根据题意得，
＝1，解得x＝27，
经检验x＝27是原方程的根，
答：乙队单独施工需要27个月才能完成任务；
（2）根据题意得，，
整理得，a＝，
∵a，b为正整数，且a≤6，b≤24，
∴b为3的倍数，
∴b＝24时，a＝2；b＝21时，a＝4；b＝18时，a＝6，
∴方案一：甲队施工2个月，乙队施工24个月；
方案二：甲队施工4个月，乙队施工21个月；
方案三：甲队施工6个月，乙队施工18个月；
设甲乙两队实际施工的费用为w万元，得，
w＝8a+5b＝8×（18﹣b）+5b＝﹣+144，
∵k＝＜0，
∴w随b的增大而减小，
即当b最大＝24时，所支付费用w最低，
∴方案一：甲队施工2个月，乙队施工24个月，所支付费用最低．
25．（2023•德阳）如图，点A在反比例函数y＝（k≠0）的图象上，点C是点A关于y轴的对称点，△OAC的面积是8．
（1）求反比例函数的解析式；
（2）当点A的横坐标为2时，过点C的直线y＝2x+b与反比例函数的图象相交于点P，求交点P的坐标．

【答案】（1）反比例函数的解析式：y＝；
（2）P（2﹣2，4+4）或（﹣2﹣2，4﹣4）．
【解答】解：（1）如图：AC与y轴交于点M，

∵C是点A关于y轴的对称点，△OAC的面积是8，
∴S△AOM＝4，
∴AM•MO＝4，
∴AM•MO＝8，
∴k＝8，
∴反比例函数的解析式：y＝；
（2）∵点A的横坐标为2，
∴x＝2时，y＝4，
∴A（2，4），
∴C（﹣2，4），
∵直线y＝2x+b过点C，
∴﹣2×2+b＝4，
b＝8，
∴直线y＝2x+8，
联立，
∴或，
∴P（2﹣2，4+4）或（﹣2﹣2，4﹣4）．
26．（2023•雅安）如图，在平面直角坐标系中，四边形OABC是边长为2的正方形，点A，C在坐标轴上，反比例函数y＝（x＞0）的图象经过点B．
（1）求反比例函数的表达式；
（2）点D在反比例函数图象上，且横坐标大于2，S△OBD＝3，求直线BD的函数表达式．

【答案】（1）反比例函数的表达式为y＝；
（2）直线BD的函数表达式为y＝﹣．
【解答】解：（1）∵四边形OABC是边长为2的正方形，
∴B（2，2），
∵反比例函数y＝（x＞0）的图象经过点B，
∴k＝2×2＝4，
∴反比例函数的表达式为y＝；
（2）作DE⊥x轴于E，
∵BA⊥x轴，
∴S△DOE＝S△AOB＝，
设D（m，），则OE＝m，DE＝，
∵S△OBD＝3，
∴S△OBD＝S△AOB+S梯形ABDE﹣S△DOE＝S梯形ABDE＝3，
∴，
整理得m2﹣3m﹣4＝0，
解得m＝4或m＝﹣1（舍去），
∴D（4，1），
设直线BD的解析式为y＝ax+b，
把B、D的坐标代入得，
解得，
∴直线BD的函数表达式为y＝﹣．
27．（2023•广元）某移动公司推出A，B两种电话计费方式．
计费方式
月使用费/元
主叫限定时间/min
主叫超时费/（元/min）
被叫
A
78
200
0.25
免费
B
108
500
0.19
免费
（1）设一个月内用移动电话主叫时间为tmin，根据上表，分别写出在不同时间范围内，方式A，方式B的计费金额y1，y2关于t的函数解析式；
（2）若你预计每月主叫时间为350min，你将选择A，B哪种计费方式，并说明理由；
（3）请你根据月主叫时间t的不同范围，直接写出最省钱的计费方式．
【答案】（1），；
（2）选择方式B计费；
（3）当0≤t＜320时，方式A更省钱；当t＝320，方式A和B的付费金额相同；当t＞320，方式B更省钱．
【解答】解：（1）设方式A的计费金额y1（元），方式B的计费金额y2（元），
根据表格数据可知，当0≤t≤200时，y1＝78；当t＞200时，y1＝78+0.25（t﹣200）＝0.25t+28；
当0≤t≤500时，y2＝108；当t＞500时，y2＝108+0.19（t﹣500）＝0.19t+13；
综上，，；
（2）选择方式B计费，理由如下：
当每月主叫时间为350min时，
y1＝0.25×350+28＝115.5，
y2＝108，
∵115.5＞108，
∴选择方式B计费；
（3）令y1＝108，得0.25t+28＝108，
解得：t＝320，
∴当0≤t＜320时，y1＜108＜y2，
∴当0≤t＜320时，方式A更省钱；
当t＝320，方式A和B的付费金额相同；
当t＞320，方式B更省钱．
28．（2023•广元）如图，已知一次函数y＝kx+6的图象与反比例函数y＝（m＞0）的图象交于A（3，4），B两点，与x轴交于点C，将直线AB沿y轴向上平移3个单位长度后与反比例函数图象交于点D，E．
​（1）求k，m的值及C点坐标；
（2）连接AD，CD，求△ACD的面积．

【答案】（1）k＝﹣，m＝12，点C的坐标为（9，0）；
（2）9．
【解答】解：（1）∵一次函数y＝kx+6的图象与反比例函数y＝（m＞0）的图象交于A（3，4），B两点，
∴4＝3k+6，4＝，
∴k＝﹣，m＝12，
∴一次函数的解析式为y＝﹣，反比例函数的解析式为y＝，
把y＝0代入y＝﹣得：0＝﹣，
解得x＝9，
∴点C的坐标为（9，0）；
（2）延长DA交x轴于点F，
将直线AB沿y轴向上平移3个单位长度后解析式为y＝﹣+3＝﹣x+9，
由，解得，
∴D（，8），
设直线AD的解析式为y＝ax+b，
把A、D的坐标代入得，
解得，
∴直线AD的解析式为y＝﹣+12，
令y＝0，则0＝﹣+12，
解得x＝，
∴F（，0），
∴CF＝9﹣＝，
∴S△ACD＝S△CDF﹣S△CAF＝﹣＝9．

29．（2023•内江）某水果种植基地为响应政府号召，大力种植优质水果．某超市看好甲、乙两种优质水果的市场价值，经调查，这两种水果的进价和售价如表所示：
水果种类
进价（元/千克）
售价（元/千克）
甲
a
20
乙
b
23
该超市购进甲种水果15千克和乙种水果5千克需要305元；购进甲种水果20千克和乙种水果10千克需要470元．
（1）求a，b的值；
（2）该超市决定每天购进甲、乙两种水果共100千克进行销售，其中甲种水果的数量不少于30千克，且不大于80千克．实际销售时，若甲种水果超过60千克，则超过部分按每千克降价3元销售，求超市当天售完这两种水果获得的利润y（元）与购进甲种水果的数量x（千克）之间的函数关系式，并写出x的取值范围；
（3）在（2）的条件下，超市在获得的利润y（元）取得最大值时，决定售出的甲种水果每千克降价3m元，乙种水果每千克降价m元，若要保证利润率（利润率＝）不低于16%，求m的最大值．
【答案】（1）a＝14；b＝19；
（2）超市当天售完这两种水果获得的利润y（元）与购进甲种水果的数量x（千克）之间的函数关系为：y＝．
（3）m的最大值为1.2．
【解答】解：（1）由题可列，
解得．
（2）由题可得当30≤x≤60时，
y＝（20﹣14）x+（23﹣19）（100﹣x）＝2x+400，
当60＜x≤80时，
y＝（20﹣3﹣14）（x﹣60）+（20﹣14）×60+（23﹣19）（100﹣x）＝﹣x+580，
答：超市当天售完这两种水果获得的利润y（元）与购进甲种水果的数量x（千克）之间的函数关系为：y＝．
（3）∵y＝，
∴当x＝60时，y的值最大，即y＝520，
由题可列×100%≥16%，
解得m≤1.2，
答：m的最大值为1.2．
30．（2023•乐山）如图，一次函数y＝kx+b的图象与反比例函数y＝的图象交于点A（m，4），与x轴交于点B，与y轴交于点C（0，3）．
（1）求m的值和一次函数的表达式；
（2）已知P为反比例函数y＝图象上的一点，S△OBP＝2S△OAC，求点P的坐标．
​

【答案】（1）m＝1，一次函数的解析式为y＝x+3；
（2）点P（2，2）或（﹣2，﹣2）．
【解答】解：（1）∵点A（m，4）在反比例函数 的图象上，
∴，
∴m＝1，
∴A（1，4），
又∵点A（1，4）、C（0，3）都在一次函数y＝kx+b的图象上，
∴，
解得，
∴一次函数的解析式为y＝x+3；
（2）对于y＝x+3，当y＝0时，x＝﹣3，
∴OB＝3，
∵C（0，3），
∴OC＝3，
过点A作 AH⊥y 轴于点H，过点P作 PD⊥x 轴于点D，
∵S△OBP＝2S△OAC，
∴，即，
解得PD＝2，
∴点P的纵坐标为2或﹣2，
将y＝2或﹣2代入 得x＝2或﹣2，
∴点P（2，2）或（﹣2，﹣2）．

31．（2023•巴中）如图，正比例函数y＝kx（k≠0）与反比例函数y＝（m≠x）的图象交于A、B两点，A的横坐标为﹣4，B的纵坐标为﹣6．
（1）求反比例函数的表达式．
（2）观察图象，直接写出不等式kx＜的解集．
（3）将直线AB向上平移n个单位，交双曲线于C、D两点，交坐标轴于点E、F，连接OD、BD，若△OBD的面积为20，求直线CD的表达式．

【答案】（1）反比例函数的表达式为y＝﹣；
（2）﹣4＜x＜0或x＞4；
（3）直线CD为y＝﹣x+10．
【解答】解：（1）∵正比例函数y＝kx（k≠0）与反比例函数y＝（m≠x）的图象交于A、B两点，
∴A、B关于原点对称，
∵A的横坐标为﹣4，B的纵坐标为﹣6，
∴A（﹣4，6），B（4，﹣6），
∵点A（﹣4，6）在反比例函数y＝（m≠x）的图象上，
∴6＝，
∴m＝﹣24，
∴反比例函数的表达式为y＝﹣；
（2）观察函数图象，可知：当﹣4＜x＜0或x＞4时，正比例函数y＝kx的图象在反比例函数y＝（m≠x）的图象下方，
∴不等式kx＜的解集为﹣4＜x＜0或x＞4；
（3）方法一：连接BE，作BG⊥y轴于点G，
∵A（﹣4，6）在直线y＝kx上，
∴6＝﹣4k，解得k＝﹣，
∴直线AB的表达式为y＝﹣x，
∵CD∥AB，
∴S△OBD＝S△OBE＝20，
∵B（4，﹣6），
∴BG＝4，
∴S△OBE＝＝20，
∴OE＝10，
.E（0，10），
∴直线CD为y＝﹣x+10．
方法二：
连接BF，作BH⊥x轴于H，
∵A（﹣4，6）在直线y＝kx上，
∴k＝﹣，
∴直线AB的表达式为y＝﹣x，
∵CD∥AB，
∴S△OBD＝S△OBF＝20，
∵B（4，﹣6），
∴OF•6＝20，
∴OF＝，
∴F（，0），
设直线CD的表达式为y＝﹣x+b，
代入F点的坐标得，﹣×+b＝0
解得b＝10，
∴直线CD为y＝﹣x+10．


32．（2023•泸州）如图，在平面直角坐标系xOy中，直线l：y＝kx+2与x，y轴分别相交于点A，B，与反比例函数y＝（x＞0）的图象相交于点C，已知OA＝1，点C的横坐标为2．
（1）求k，m的值；
（2）平行于y轴的动直线与l和反比例函数的图象分别交于点D，E，若以B，D，E，O为顶点的四边形为平行四边形，求点D的坐标．

【答案】（1）k＝2，m＝12；
（2）（，2+2）或（﹣1，2）．
【解答】解：（1）∵OA＝1，
∴点A的坐标为（﹣1，0），
则﹣k+2＝0，
解得：k＝2，
∴直线l的解析式为y＝2x+2，
∵点C在直线l上，点C的横坐标为2，
∴点C的纵坐标为2×2+2＝6，
∴点C的坐标为（2，6），
∴m＝2×6＝12；
（2）设点D的坐标为（n，2n+2），则点E的坐标为（n，），
∴DE＝|2n+2﹣|，
∵OB∥DE，
∴当OB＝DE时，以B，D，E，O为顶点的四边形为平行四边形，
∵直线y＝2x+2与y轴交于点B，
∴OB＝2，
∴|2n+2﹣|＝2，
当2n+2﹣＝2时，n1＝，n2＝﹣（舍去），
此时，点D的坐标为（，2+2），
当2n+2﹣＝﹣2时，n1＝﹣1，n2＝﹣﹣1（舍去），
此时，点D的坐标为（﹣1，2），
综上所述：以B，D，E，O为顶点的四边形为平行四边形时，点D的坐标为（，2+2）或（﹣1，2）．
33．（2023•德阳）已知：在平面直角坐标系中，抛物线与x轴交于点A（﹣4，0），B（2，0），与y轴交于点C（0，﹣4）．
（1）求抛物线的解析式；
（2）如图1，如果把抛物线x轴下方的部分沿x轴翻折180°，抛物线的其余部分保持不变，得到一个新图象．当平面内的直线y＝kx+6与新图象有三个公共点时，求k的值；
（3）如图2，如果把直线AB沿y轴向上平移至经过点D，与抛物线的交点分别是E，F，直线BC交EF于点H，过点F作FG⊥CH于点G，若，求点F的坐标．
​
【答案】（1）y＝x2+x﹣4；
（2）k＝1或；
（3）（4，8）．
【解答】解：（1）设抛物线解析式为y＝a（x+4）（x﹣2），
将点C（0，﹣4）代入y＝a（x+4）（x﹣2），
∴﹣8a＝﹣4，
解得a＝，
∴抛物线的解析式为y＝（x+4）（x﹣2）＝x2+x﹣4；
（2）抛物线沿x轴翻折后的函数解析式为y＝﹣x2﹣x+4，
当k＞0时，
当直线y＝kx+6经过点A（﹣4，0）时，﹣4k+6＝0，解得k＝，此时函数与直线有三个交点；
当kx+6＝﹣x2﹣x+4有两个相同的实数根时，Δ＝（k+1）2﹣4＝0，
解得k＝1或k＝﹣3（舍），
当0＜k＜1时，直线y＝kx+6与翻折后的抛物线部分没有公共点，与原抛物线未翻折部分有2个公共点，即直线y＝kx+6与新图象只有2个公共点，不符合题意；
当1＜k＜时，直线y＝kx+6与翻折后的抛物线部分有2个公共点，与原抛物线未翻折部分有2个公共点，即直线y＝kx+6与新图象有4个公共点，不符合题意；
当k＞时，直线y＝kx+6与翻折后的抛物线部分有1个公共点，与原抛物线未翻折部分的右侧有1个公共点，即直线y＝kx+6与新图象有2个公共点，不符合题意；
∴当k＝1或时，直线y＝kx+6与新图象有三个公共点；
当k＜0时，
当kx+6＝﹣x2﹣x+4有一个解时，Δ＝（k+1）2﹣4＝0，
解得k＝1（舍）或k＝﹣3，
当k＝﹣3时，直线y＝kx+6与翻折后的抛物线部分只有1个公共点（2，0），与原抛物线y＝x2+x﹣4未翻折部分有2个公共点（﹣10，36）和（2，0），即直线y＝kx+6与新图象只有2个公共点，不符合题意；
当k＜﹣3时，直线y＝kx+6与翻折后的抛物线部分只有1个公共点，与原抛物线未翻折部分左侧有1个公共点，即直线y＝kx+6与新图象只有2个公共点，不符合题意；
当﹣3＜k＜0时，直线y＝kx+6与翻折后的抛物线部分没有公共点，与原抛物线未翻折部分有2个公共点，即直线y＝kx+6与新图象只有2个公共点，不符合题意；
综上所述：当直线y＝kx+6与新图象有三个公共点时，k＝1或；
（3）设D（0，t），则H（2+t，t），
∵EF∥AB，
∴∠FHG＝∠OBC，
∵FG⊥CH，
∴tan∠FHG＝tan∠OBC＝2，
∴FG＝2HG，
∴HG＝FH，
∵，
∴DF＝2FH，
∴DF＝DH，
∵DH＝2+t，
∴FD＝（t+4），
∴F（t+，t），
当x2+x﹣4＝t时，x＝t+是方程的一个根，
∴t2﹣6t﹣32＝0，
解得t＝﹣4（舍）或t＝8，
∴F（4，8）．
34．（2023•雅安）在平面直角坐标系中，已知抛物线y＝x2+bx+c过点A（0，2），对称轴是直线x＝2．
（1）求此抛物线的函数表达式及顶点M的坐标；
（2）若点B在抛物线上，过点B作x轴的平行线交抛物线于点C，当△BCM是等边三角形时，求出此三角形的边长；
（3）已知点E在抛物线的对称轴上，点D的坐标为（1，﹣1）是否存在点F，使以点A，D，E，F为顶点的四边形为菱形？若存在，请直接写出点F的坐标；若不存在，请说明理由．

【答案】（1）y＝x2﹣4x+2，M（2，2）；
（2）2；
（3）存在，（﹣1，0）或（1，5）或（3，﹣1+）或（3，﹣1﹣）．
【解答】解：（1）∵对称轴是直线x＝2，
∴﹣＝2，
解得b＝﹣4，
∴y＝x2﹣4x+c，
将点A代入y＝x2﹣4x+c，可得c＝2，
∴函数的解析式为y＝x2﹣4x+2，
当x＝2时，y＝﹣2，
∴顶点M（2，﹣2）；
（2）设直线BC所在的直线为y＝m，
当x2﹣4x+2＝m时，xB+xC＝4，xB•xC＝2﹣m，
∴|xB﹣xC|＝2，
∵M（2，﹣2），
∴M点到直线BC的距离为m+2，
∵△BCM是等边三角形，
∴|xB﹣xC|＝（m+2），即＝（m+2），
解得m＝1或m＝﹣2（舍），
∴三角形的边长为2；
（3）在点F，使以点A，D，E，F为顶点的四边形为菱形，理由如下：
设E（2，t），F（x，y），
①当AD为菱形对角线时，AE＝DE，
，
解得，
∴F（﹣1，0）；
②当AE为菱形对角线时，AD＝DE，
∴，
解得（舍）或，
∴F（1，5）；
③当AF为菱形对角线时，AE＝AD，
∴，
解得或，
∴F（3，﹣1+）或（3，﹣1﹣）；
综上所述：F点坐标为（﹣1，0）或（1，5）或（3，﹣1+）或（3，﹣1﹣）．
35．（2023•巴中）在平面直角坐标系中，抛物线y＝ax2+bx+c（a≠0）经过点A（﹣1，0）和B（0，3），其顶点的横坐标为1．
（1）求抛物线的表达式．
（2）若直线x＝m与x轴交于点N，在第一象限内与抛物线交于点M，当m取何值时，使得AN+MN有最大值，并求出最大值．
（3）若点P为抛物线y＝ax2+bx+c（a≠0）的对称轴上一动点，将抛物线向左平移1个单位长度后，Q为平移后抛物线上一动点．在（2）的条件下求得的点M，是否能与A、P、Q构成平行四边形？若能构成，求出Q点坐标；若不能构成，请说明理由．

【答案】（1）y＝﹣x2+2x+3；
（2）当m＝时，AN+MN有最大值，最大值为；
（3）存在以A，P，Q，M为顶点的平行四边形，点Q的坐标为（﹣，）或（﹣，）或（，﹣）．
【解答】解：（1）∵抛物线的顶点横坐标为1，
∴抛物线的对称轴为直线x＝1．
∵点A的坐标为（﹣1，0），
∴抛物线与x轴的另一交点坐标为（3，0）．
将（﹣1，0），（3，0），（0，3）代入y＝ax2+bx+c得：，
解得：，
∴抛物线的表达式为y＝﹣x2+2x+3；
（2）∵直线x＝m与x轴交于点N，在第一象限内与抛物线交于点M，
∴点M的坐标为（m，﹣m2+2m+3），点N的坐标为（m，0），
∴MN＝﹣m2+2m+3，AN＝m+1，
∴AN+MN＝m+1+（﹣m2+2m+3）＝﹣m2+3m+4＝﹣（m﹣）2+，
∵﹣1＜0，且0＜m＜3，
∴当m＝时，AN+MN有最大值，最大值为；
（3）∵y＝﹣x2+2x+3＝﹣（x﹣1）2+4，
∴抛物线向左平移1个单位长度后的表达式为y＝﹣x2+4．
当x＝时，y＝﹣（）2+2×+3＝，
∴点M的坐标为（，）．
假设存在以A，P，Q，M为顶点的平行四边形，设点P的坐标为（1，m），点Q的坐标为（n，﹣n2+4）．
①当AM为对角线时，对角线AM，PQ互相平分，
∴＝，
解得：n＝﹣，
∴点Q的坐标为（﹣，）；
②当AP为对角线时，对角线AP，MQ互相平分，
∴＝，
解得：n＝﹣，
∴点Q的坐标为（﹣，）；
③当AQ为对角线时，对角线AQ，PM互相平分，
∴＝，
解得：n＝，
∴点Q的坐标为（，﹣）．
综上所述，存在以A，P，Q，M为顶点的平行四边形，点Q的坐标为（﹣，）或（﹣，）或（，﹣）．
36．（2023•广元）如图1，在平面直角坐标系中，已知二次函数y＝ax2+bx+4的图象与x轴交于点A（﹣2，0），B（4，0），与y轴交于点C．
（1）求抛物线的解析式；
（2）已知E为抛物线上一点，F为抛物线对称轴l上一点，以B，E，F为顶点的三角形是等腰直角三角形，且∠BFE＝90°，求出点F的坐标；
（3）如图2，P为第一象限内抛物线上一点，连接AP交y轴于点M，连接BP并延长交y轴于点N，在点P运动过程中，OM+ON是否为定值？若是，求出这个定值；若不是，请说明理由．

【答案】（1）抛物线解析式为y＝﹣x2+x+4；
（2）F（1，1）或（1，﹣5）或（1，﹣3）或（1，3）；
（3）OM+ON为定值6．
【解答】解：（1）将点A（﹣2，0），B（4，0），代入 y＝ax2+bx+4得：
，
解得：，
∴抛物线解析式为y＝﹣x2+x+4；
（2）∵点 A（﹣2，0），B（4，0），
∴抛物线的对称轴为直线l：，
设直线l与x轴交于点G，过点E作 ED⊥l于点D，
当F在x轴上方时，如图：

∵以B，E，F为顶点的三角形是等腰直角三角形，且∠BFE＝90°，
∴EF＝BF，
∵∠DFE＝90°﹣∠BFG＝∠GBF，∠EDF＝∠BGF＝90°，
∴△DFE≌△GBF（AAS），
∴GF＝DE，GB＝FD，
设F（1，m），则DE＝m，DG＝DF+FG＝GB+FG＝3+m，
∴E（1+m，3+m），
∵E点在抛物线y＝﹣x2+x+4上，
∴，
解得：m＝﹣3（舍去）或m＝1，
∴F（1，1）；
当F在x轴下方时，如图：

同理可得△DFE≌△GBF（AAS），GF＝DE，GB＝FD，
设F（1，n），则E（1﹣n，n﹣3），
把E（1﹣n，n﹣3）代入y＝﹣x2+x+4得：
n﹣3＝﹣（1﹣n）2+（1﹣n）+4，
解得n＝3（舍去）或n＝﹣5，
∴F（1，﹣5）；
当E点与A点重合时，如图所示，

∵AB＝6，△ABF是等腰直角三角形，且∠BFE＝90°，
∴，
此时 F（1，﹣3），
由对称性可得，点F'（1，3）也满足条件，
综上所述，F（1，1）或（1，﹣5）或（1，﹣3）或（1，3）；
（3）OM+ON为定值6，理由如下：
设P（s，t），直线AP的解析式为 y＝dx+f，BP的解析式为 y＝gx+h，
∵点 A（﹣2，0），B（4，0），P（s，t），
∴，，
解得：，，
∴直线AP的解析式为 ，BP的解析式为y＝x+，
在中，令 x＝0 得，
∴，
在中，令x＝0得，
∴N（0，），
∵P（s，t） 在抛物线上，
∴t＝﹣s2+s+4＝﹣（s﹣4）（s+2），
∴OM+ON＝+×＝＝＝6，
∴OM+ON为定值6．
37．（2023•乐山）已知（x1，y1），（x2，y2）是抛物线C1：y＝﹣x2+bx（b为常数）上的两点，当x1+x2＝0时，总有y1＝y2．
（1）求b的值；
（2）将抛物线C1平移后得到抛物线C2：y＝﹣（x﹣m）2+1（m＞0）．
当0≤x≤2时，探究下列问题：
①若抛物线C1与抛物线C2有一个交点，求m的取值范围；
②设抛物线C2与x轴交于A，B两点，与y轴交于点C，抛物线C2的顶点为点E，△ABC外接圆的圆心为点F．如果对抛物线C1上的任意一点P，在抛物线C2上总存在一点Q，使得点P、Q的纵坐标相等．求EF长的取值范围．
【答案】（1）b＝0；
（2）①2≤m≤2+2；
②．
【解答】解：（1）由题可知：y1＝﹣+bx1，y2＝﹣+bx2，
∵当x1+x2＝0 时，总有 y1＝y2，
∴﹣+bx1＝﹣+bx2，
整理得：（x1﹣x2）（x1+x2﹣4b）＝0，
∵x1≠x2，
∴x1﹣x2≠0，
∴x1+x2﹣4b＝0，
∴b＝0；
（2）①注意到抛物线 C2 最大值和开口大小不变，m只影响图象左右平移．
下面考虑满足题意的两种临界情形：
（i）当抛物线 C2 过点（0，0）时，如图1所示，

此时，x＝0，，解得m＝2或﹣2（舍）．
（i）当抛物线 C2 过点（2，﹣1）时，如图2所示，

此时，x＝2，
解得 或 （舍）．
综上所述，2≤m≤2+2；
②同①考虑满足题意的两种临界情形：
（i）当抛物线 C2 过点（0，﹣1）时，如图3所示，

此时，x＝0，，解得 或 （舍）．
（ii）当抛物线 C2 过点（2，0）时，如图4所示，

此时，x＝2，，解得 m＝4 或0（舍）．
综上所述，．
如图5，由圆的性质可知，点E、F在线段AB的垂直平分线上，

，解得 xA＝m﹣2，xB＝m+2，
∴HB＝m+2﹣m＝2，
∵FB＝FC．
∴FH2+HB2＝FG2+GC2，
设FH＝t，
∴t2+22＝（﹣1﹣t）2+m2，
∴（﹣1）2﹣2（﹣1）t+m2﹣4＝0，
∴（﹣1）（﹣2t+3）＝0，
∵m≥2，
∴﹣1≠0，
∴，即 ，
∵
∴，即＜FH≤，
∵EF＝FH+1，
∴．
38．（2023•内江）如图，在平面直角坐标系中，抛物线y＝ax2+bx+c与x轴交于B（4，0），C（﹣2，0）两点，与y轴交于点A（0，﹣2）．
（1）求该抛物线的函数表达式；
（2）若点P是直线AB下方抛物线上的一动点，过点P作x轴的平行线交AB于点K，过点P作y轴的平行线交x轴于点D，求的最大值及此时点P的坐标；
（3）在抛物线的对称轴上是否存在一点M，使得△MAB是以AB为一条直角边的直角三角形；若存在，请求出点M的坐标，若不存在，请说明理由．

【答案】（1）y＝x2﹣x﹣2；
（2）最大值为，此时P（，﹣）；
（3）存在，M的坐标为（1，6）或（1，﹣4）．
【解答】解：（1）由题意，，
解得，
∴抛物线的解析式为y＝x2﹣x﹣2；

（2）∵A（0，﹣2），B（4，0），
∴直线AB的解析式为y＝x﹣2，
设P （0＜m＜4），则，
∴PK+PD＝（m﹣m2+m）+（﹣+m+2）＝﹣m2+m+2＝﹣（m﹣）2+，
∵﹣＜0，
∴当m＝时，PK+PD有最大值，最大值为，此时P（，﹣）；

（3）存在．过A作AM2⊥AB交抛物线的对称轴于M2，过B作BM1⊥AB交抛物线的对称轴于点M1，连接AM1，BM2，设M1（1，n），则＝n2+4n+5，＝n2+9，

由AB2+＝，可得22+42+n2+9＝n2+4n+5，
∴n＝6，
∴M1（1，6），
∴直线 BM1 解析式为y＝﹣2x+8，
∵AM2∥BM1，且经过A（0，﹣2），
∴直线 AM2 解析式为y＝﹣2x﹣2，
∴当x＝1时，y＝﹣2×1﹣2＝﹣4，
∴M2（1﹣4），
综上所述：存在，M的坐标为（1，6）或（1，﹣4）