2022-2023学年陕西省咸阳市武功县高二下学期期中数学（理）试题含答案

2022-2023学年陕西省咸阳市武功县高二下学期期中数学（理）试题

一、单选题

1．在复平面内，复数对应的点位于（    ）

A．第一象限 B．第二象限

C．第三象限 D．第四象限

【答案】B

【详解】利用复数的四则运算化简，再根据复数的几何意义即可得解.

【分析】因为，

所以对应的点为，它位于第二象限.

故选：B

2．已知是定义在R上的可导函数，若，则（    ）

A． B． C．1 D．

【答案】D

【分析】根据极限与导数的定义计算．

【详解】.

故选：D.

3．有一机器人的运动方程为，（t是时间，s是位移），则该机器人在时刻时的瞬时速度为（    ）

A．5 B．7 C．10 D．13

【答案】C

【分析】对运动方程求导，根据导数的意义，将代入导函数即可求解.

【详解】因为，所以，

则，

所以该机器人在时刻时的瞬时速度为，

故选：.

4．下列三句话按“三段论”的表述形式，排列顺序正确的是（    ）

①是偶函数；②的图像关于y轴对称；③偶函数的图像关于y轴对称．

A．①→②→③ B．③→②→① C．②→①→③ D．③→①→②

【答案】D

【分析】根据“三段论”的结构即可求解.

【详解】根据“三段论”：“大前提”，“小前提”则“结论”可知：偶函数的图像关于y轴对称是“大前提”，是偶函数是“小前提”，的图像关于y轴对称是“结论”，

故选：D

5．函数的图像如图所示，下列不等关系正确的是（    ）

A． B．

C． D．

【答案】C

【分析】根据图象观察斜率的大小以及导数的几何意义可得答案.

【详解】从的图象可以看出，点处切线的斜率大于直线的斜率，直线的斜率大于点处切线的斜率，点处切线的斜率大于0，

根据导数的几何意义可得，即.

故选：C

6．已知复数z满足，复数复数z的共轭复数，则复数的虚部为（    ）

A． B． C． D．

【答案】B

【分析】利用复数的运算及基本概念求解即可.

【详解】解：根据题意，.

所以，复数的虚部为.

故选：B.

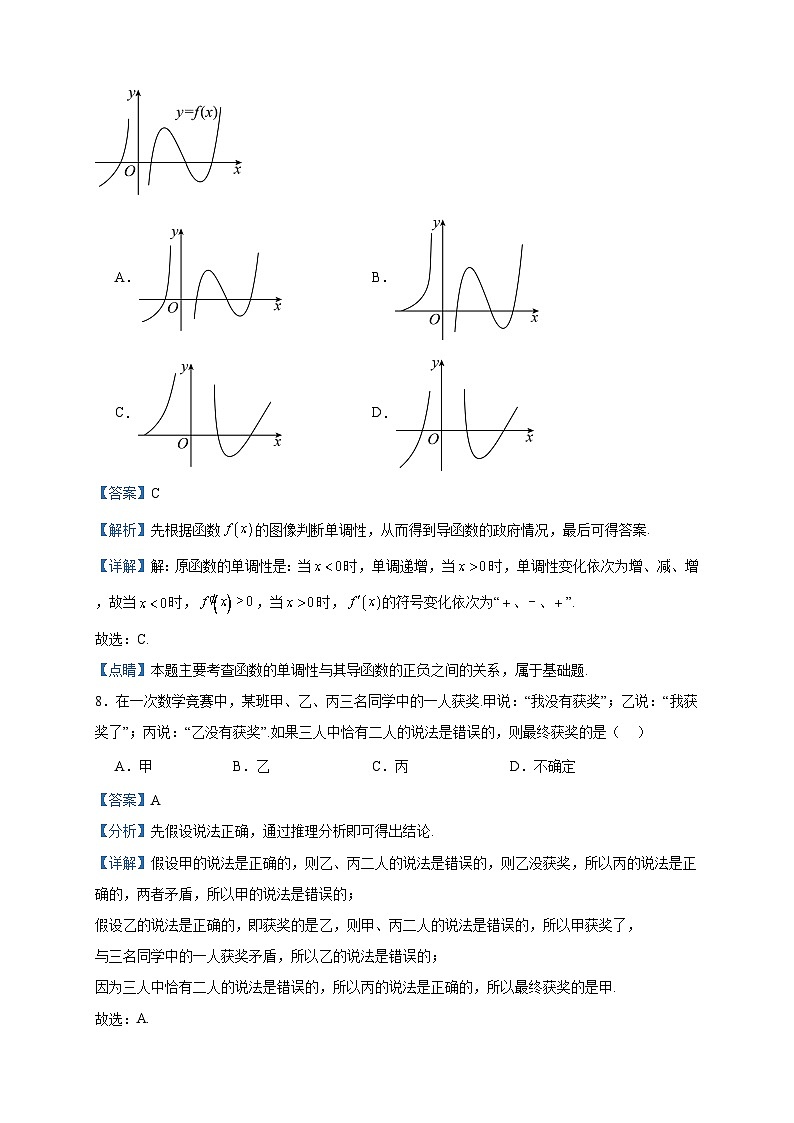
7．设函数在定义域内可导，的图象如图所示，则导函数的图象可能是（　　）

A．   B．  

C．   D．  

【答案】C

【解析】先根据函数的图像判断单调性，从而得到导函数的政府情况，最后可得答案.

【详解】解：原函数的单调性是：当时，单调递增，当时，单调性变化依次为增、减、增，故当时，，当时，的符号变化依次为“、、”.

故选：C.

【点睛】本题主要考查函数的单调性与其导函数的正负之间的关系，属于基础题.

8．在一次数学竞赛中，某班甲、乙、丙三名同学中的一人获奖.甲说：“我没有获奖”；乙说：“我获奖了”；丙说：“乙没有获奖”.如果三人中恰有二人的说法是错误的，则最终获奖的是（    ）

A．甲 B．乙 C．丙 D．不确定

【答案】A

【分析】先假设说法正确，通过推理分析即可得出结论.

【详解】假设甲的说法是正确的，则乙、丙二人的说法是错误的，则乙没获奖，所以丙的说法是正确的，两者矛盾，所以甲的说法是错误的；

假设乙的说法是正确的，即获奖的是乙，则甲、丙二人的说法是错误的，所以甲获奖了，

与三名同学中的一人获奖矛盾，所以乙的说法是错误的；

因为三人中恰有二人的说法是错误的，所以丙的说法是正确的，所以最终获奖的是甲.

故选：A.

9．我们知道：在平面内，点到直线的距离公式为，通过类比的方法，则：在空间中，点到平面的距离为（    ）

A．7 B．5 C．3 D．

【答案】B

【分析】利用平面内点到直线的距离公式类比得到空间中点到平面的距离公式进而可以求解.

【详解】平面内点到直线的距离公式，

类比平面内点到直线的距离公式，可得空间中点到直线的距离为：.

故选：B.

10．给定函数，则下列结论不正确的是（    ）

A．函数有两个零点

B．函数在上单调递增

C．函数的最小值是

D．当或时，方程有一个解

【答案】A

【分析】解方程，可判断A选项；利用函数的单调性与导数的关系可判断B选项；利用导数法求出函数的最小值，可判断C选项；作出函数与的图象，可判断D选项.

【详解】对于A选项，令，可得，即函数有且只有一个零点，A错；

对于B选项，对任意的恒成立，

所以，函数在上单调递增，B对；

对于C选项，因为，则，

由可得，由可得，

所以，函数的减区间为，增区间为，

所以，函数的最小值为，C对；

对于D选项，当时，；当时，，

如下图所示：

当或时，直线与函数的图象有且只有一个交点，D对.

故选：A.

11．已知函数，若存在，使得有解，则实数a的取值范围是（    ）

A． B．

C． D．

【答案】C

【分析】根据题意，转化为在有解，设，利用导数求得函数的单调性与最大值，即可求解.

【详解】若存在，使得有解，

由函数，即，即在有解，

设，可得，

当时，，单调递增；

当时，，单调递减，

所以当时，函数取得极大值，也为最大值，即，

所以，即实数a的取值范围是.

故选：C.

12．已知是函数的导函数，且对于任意的有.请你试用构造函数的方法，利用函数的单调性判断下列不等式一定成立的是（    ）

A． B．

C． D．

【答案】A

【分析】设，，根据已知条件，利用导数得到为增函数，由可推出A；由可推出B；由可推出C；由可推出D.

【详解】因为，所以，所以为偶函数，

则对于任意的有，

即为对于任意的有，

设，，则，

因为当时，，所以，

所以在上为增函数，

因为，所以，所以，

所以，

所以，故A正确；

因为，所以，所以，

所以，所以，故B不正确；

因为，所以，所以，

所以，所以，故C不正确；

因为，所以，所以，

所以，所以，故D不正确.

故选：A.

【点睛】关键点点睛：构造函数，，利用导数判断函数在上的单调性是解决本题的关键.

二、填空题

13．若，则          ．

【答案】

【分析】根据复数代数形式的除法运算法则化简复数，再求出其模.

【详解】因为，所以，

所以.

故答案为：

14．函数的极小值是            .

【答案】

【分析】求导，再根据极小值的定义即可得解.

【详解】，

令，得或，令，得，

所以函数在上单调递增，在上单调递减，

所以函数的极小值是.

故答案为：.

15．已知函数及其导函数满足，则            .

【答案】/

【分析】在等式两边求导，再令，可得出关于的等式，即可解得的值.

【详解】因为，则，所以，，

解得.

故答案为：.

16．定义：设函数在上的导函数为，若在上也存在导函数，则称函数在上存在二阶导函数，简记为．若在区间上，则称函数在区间上为“凹函数”．已知在区间上为“凹函数”，则实数的取值范围为          ．

【答案】

【分析】根据“凹函数”的定义，化为恒成立，再构造函数，，利用导数求出其最小值可得结果.

【详解】因为，所以，

所以，

因为在区间上为“凹函数”，

所以，所以，

令，

则，

令，得，令,得，

所以在上为减函数，在上为增函数，

所以，

所以.

故答案为：

三、解答题

17．求下列函数的导数:

(1)；

(2).

【答案】(1)

(2)

【分析】（1）（2）根据已知条件，结合导数的运算法则，准确计算，即可求解.

【详解】（1）解：由函数，

所以.

（2）解：由函数，

可得.

18．设复数（其中），，i为虚数单位.

(1)若是实数，求的值；

(2)若是纯虚数，求的值.

【答案】(1)

(2)

【分析】（1）是实数，说明虚部为，可求出的值，再去计算即可

（2）先将进行化简，因为是纯虚数，说明实部为，且虚部不为，从而求出.

【详解】（1）（其中），，

，

由是实数，所以，解得．

，，

则；

（2）由是纯虚数，

得，解得．

19．已知函数.

(1)求函数图象在处的切线方程:

(2)若函数有两个零点，求m的值.

【答案】(1)

(2)或

【分析】（1）求导，得到，求出，得到切线方程；

（2）对求导，得到其单调性，确定或，求出答案.

【详解】（1），故，

又，故图象在处的切线方程为，

即；

（2），

令，

当或时，，单调递增，当时，，单调递减，

且时，，时，，

若有两个零点，则必有或，

即或，解得或，

故m的值为或

20．（1）已知为正数，，，用反证法证明：a，b中至少有一个不小于6；

（2）用分析法证明：当时，.

【答案】（1）（2）证明见解析

【分析】（1）假设均小于，则，再由基本不等式证明得矛盾，即可得证；

（2）利用分析法从结论往前推即可.

【详解】（1）假设均小于，即，则，

而，，

则，

当且仅当，即时，取等号，

与假设矛盾，

所以a，b中至少有一个不小于6；

（2）当时，要证，

需证，

只需证，

即证，

也就是证，

即证，此式显然成立，

所以.

21．已知函数，，函数在处有极值．

(1)求函数的解析式；

(2)求函数在上的最值．

【答案】(1)；

(2)最小值为，最大值为．

【分析】（1）因在处有极值，则，得，

后检验满足题意即可；

（2）由（1），利用导数可求得在上的最值．

【详解】（1）由题，.

因在处有极值，则.

又时，，，

因时，，时，.

得在上单调递增，在上单调递减，

则函数在处有极大值，满足题意，故.

（2）当时，令，得，

令，得.

故在上单调递增，在上单调递减.

则，

.

故函数在上的最大值为，最小值.

22．已知函数（且）.

(1)讨论函数的单调性；

(2)设.求证：当时，恒成立.

【答案】(1)答案见解析

(2)证明见解析

【分析】（1）求得，对实数的取值进行分类讨论，分析导数的符号变化，由此可得出函数的增区间和减区间；

（2）令，利用导数求出函数在上的最小值，即可证得结论成立.

【详解】（1）解：因为（且），则.

①当时，，此时，函数的减区间为；

②当时，由可得，由可得.

此时，函数的增区间为，减区间为.

综上所述，当时，函数的减区间为，无增区间；

当时，函数的增区间为，减区间为.

（2）解：令，即证：当时，.

，令，则对任意的恒成立，

所以，函数在上单调递减，

因为，，所以，存在，使得，

且当时，，此时函数单调递增，

当时，，此时函数单调递减，

又因为，，所以，当时，，

故当时，.

【点睛】方法点睛：利用导数证明不等式问题，方法如下：

（1）直接构造函数法：证明不等式（或）转化为证明（或），进而构造辅助函数；

（2）适当放缩构造法：一是根据已知条件适当放缩；二是利用常见放缩结论；

（3）构造“形似”函数，稍作变形再构造，对原不等式同解变形，根据相似结构构造辅助函数.