2022-2023学年重庆市渝东九校高二下学期期中数学试题含答案

这是一份2022-2023学年重庆市渝东九校高二下学期期中数学试题含答案，共14页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。
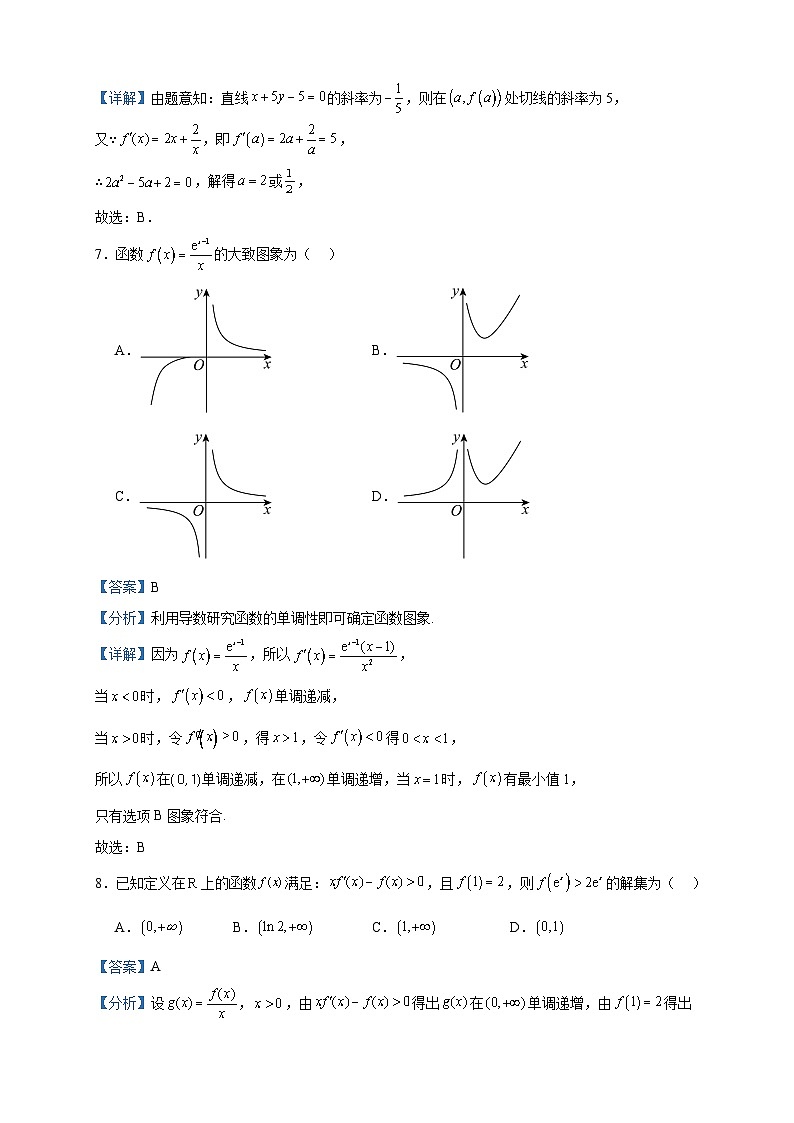
2022-2023学年重庆市渝东九校高二下学期期中数学试题 一、单选题1．若，则（    ）A．2 B．3 C．2或4 D．3或4【答案】C【分析】根据组合数公式的性质求解即可【详解】因为，所以或，故选：C2．下列函数的求导正确的是（    ）A． B．C． D．【答案】D【分析】根据常见初等函数的求导公式及复合函数求导公式可得结果．【详解】对于A：，故A不正确；对于B：，故B不正确；对于C：，故C不正确；对于D：，故D正确，故选：D．3．已知，，则等于（    ）A． B． C． D．【答案】B【分析】直接根据条件概率公式计算即可．【详解】因为，，所以，即，故选：B．4．中国古代中的“礼、乐、射、御、书、数”合称“六艺”.“礼”，主要指德育；“乐”，主要指美育；“射”和“御”，就是体育和劳动；“书”，指各种历史文化知识；“数”，指数学.某校国学社团开展“六艺”课程讲座活动，每艺安排一节，连排六节，一天课程讲座排课有如下要求：“乐”和“书”两门课程相邻排课，则“六艺”课程讲座不同的排课顺序共有（    ）A．240种 B．36种 C．120种 D．360种【答案】A【分析】对于相邻元素应用捆绑法来解决即可．【详解】“乐”和“书”两门课程相邻排课，则“六艺”课程讲座不同的排课顺序共有排法．故选：A．5．随机变量的分布如下表，其中成等差数列，且，123则（    ）A． B． C． D．1【答案】C【分析】根据分布列的性质及条件列方程组求出，再求数学期望即可．【详解】由题意得，得，则．故选：C．6．若函数的图象在处的切线与直线垂直，则的值为（    ）A． B．2或 C．2 D．1或【答案】B【分析】由两线垂直可知处切线的斜率为5，利用导数的几何意义有，即可求的值.【详解】由题意知：直线的斜率为，则在处切线的斜率为5，又∵，即，∴，解得或，故选：B．7．函数的大致图象为（    ）A． B．C． D．【答案】B【分析】利用导数研究函数的单调性即可确定函数图象.【详解】因为，所以，当时，，单调递减，当时，令，得，令得，所以在单调递减，在单调递增，当时，有最小值1，只有选项B图象符合.故选：B8．已知定义在上的函数满足：，且，则的解集为（    ）A． B． C． D．【答案】A【分析】设，，由得出在单调递增，由得出，将转化为即可得出答案．【详解】设，，因为，所以，所以在单调递增，因为，所以，由，且得，则，所以，又在单调递增，所以，故选：A． 二、多选题9．关于的展开式，下列判断正确的是（    ）A．展开式共有6项B．展开式的各二项式系数的和为32C．展开式的第4项的二项式系数为20D．展开式的各项系数的和为【答案】ABD【分析】二局二项式定理的性质逐项判断即可．【详解】对于A：展开式共有项，故A正确；对于B：展开式的各二项式系数的和为，故B正确；对于C：展开式第4项的二项式系数为，故C错误；对于D：令，得展开式的各项系数的和为，故D正确；故选：ABD．10．距离高考不到1天时，国家教育部发布了《中国高考报告》，年的高考对各科都有重大的调整，为让高二的学生各科的调整有所了解，某学校拟在一周内组织数学、英语、语文、物理、化学的位该学科的骨干教师进行“中国高考报告”的相应学科讲座，每天一科，连续天.则下列结论正确的是（    ）A．从五位教师中选两位的不同选法共有种B．数学不排在第一天的不同排法共有种C．数学、英语、语文排在都不相邻的三天的不同排法共有种D．物理要排在化学的前面（可以不相邻）的排法共有种【答案】BC【分析】直接利用组合计数原理可判断A选项；先排数学，再排其他四门学科，结合分步乘法计数原理可判断B选项；先排数学、英语、语文三门学科，再排其他两门学科，结合结合分步乘法计数原理可判断C选项；利用倍缩法可判断D选项.【详解】对于A选项，从五位教师中选两位的不同选法共有种，A错；对于B选项，数学不排在第一天，则数学有种排法，其他门学科全排即可，所以，不同的排法种数为种，B对；对于C选项，数学、英语、语文排在都不相邻的三天，则这三门学科分别排在第一、三、五天，所以，不同的排法种数为种，C对；对于D选项，物理要排在化学的前面（可以不相邻）的排法种数为种，D错.故选：BC.11．如图是的导函数的图象，对于下列四个判断，其中正确的判断是（    ）  A．当时，取得极小值B．当时，取得极大值C．在上是减函数D．在上是减函数，在上是增函数【答案】BD【分析】根据图象可得出在各个区间上的符号，从而得到单调区间，进而得到极值点.【详解】由图象知，当和时，恒成立，当和时，恒成立，即在上单调递增，在上单调递减，故C错误，D正确；所以当和时，取得极大值，当时，取得极小值，故A错误，B正确.故选：BD.12．已知函数有两个极值点，，则（    ）A．a的取值范围为（－∞，1） B．C． D．【答案】BCD【分析】利用导数判断函数的单调性，根据零点的个数求出的取值范围，进而确定的取值范围，再利用不等式的性质、构造函数利用导数逐一判断即可.【详解】由题设，且定义域为，则，当时，则单调递增，不可能存在两个零点，即不可能存在两个极值点，A错误；当时，即单调递增，当时，即单调递减，即，当时，，所以至多有一个零点；当时，，而，当趋向于0时趋于负无穷大，当趋向于正无穷时趋于负无穷大，综上，，在内各有一个零点，且，B：由且趋向于0时趋于负无穷大，所以，故，令，，又，所以单调递减，故当时，，又，所以，而，因此，故正确；C：，令，显然有，令，显然，因此有：，设，则，当时，单调递减，当时，单调递增，因为，所以，令，即，因为，所以单调递增，因为，所以，而，所以，因为，所以，当时，单调递减，因此有，即，正确；D：由，则，故，正确.故选：BCD【点睛】关键点睛：构造函数、、，利用导数研究单调性，根据单调性进行求解. 三、填空题13．已知，则           .【答案】8【分析】根据期望的性质求解即可【详解】因为，所以，故答案为：814．函数的单调增区间为            .【答案】【分析】利用导数求出函数的增区间作答.【详解】函数的定义域为，，由得，即单调递增区间为.故答案为：.15．在三个地区爆发了甲流，这三个地区分别有3%，4%，5%的人患了甲流，假设这三个地区的人口比例为5：8：7，现从这三个地区中任意选取一个人，则这个人患甲流的概率为           .【答案】【分析】利用互斥事件和独立事件的概率公式结合题意直接求解即可【详解】由题意可知，现从这三个地区中任意选取一个人，则这个人患甲流的概率为，故答案为：16．已知函数，若对任意都存在，使成立，则实数的取值范围是           .【答案】【分析】根据题意，问题转化为存在，使，判断出，从而分离出，构造函数并利用导数得到取值范围，得到关于的不等式，解得的范围.【详解】对任意都存在使成立，而，所以，即存在，使，此时，，所以，因此将问题转化为：存在，使成立，设，，当，，单调递增，所以，由题意，所以，所以实数的取值范围是.故答案为：. 四、解答题17．（1）计算；（2）已知，求的值.【答案】（1），（2）【分析】（1）利用排列数与组合数公式计算即可；（2）利用赋值法求解.【详解】（1）；（2）令，得.18．已知函数，且.(1)求的值；(2)求函数在区间上的最大值和最小值.【答案】(1)2(2)最大值为，最小值为0. 【分析】（1）求导，根据求出的值；（2）求导，得到函数单调性，极值，求出端点值，比较后求出最值.【详解】（1），，解得.（2），，，，当时，或，当时，，故在，上单调递增，在上单调递减，故在处取得极小值，在处取得极大值，又，，，，在区间上的最大值为，最小值为0.19．某学校的高二年级有5名数学老师，其中男老师3人，女老师2人.(1)如果任选3人参加校级技能大赛，所选3人中女老师人数为，求的分布列；(2)如果依次抽取2人参加市级技能大赛，求在第1次抽到男老师的条件下，第2次抽到也是男老师的概率.【答案】(1)见解析(2) 【分析】（1）的所有可能取值为0，1，2，求出概率得到分布列．（2）利用条件概率转化求解即可．【详解】（1）由题可知的所有可能取值为0，1，2，依题意得：，，，的分布列为：012（2）设第1次抽到男老师为事件，第2次抽到男老师为事件，则第1次和第2次都抽到男老师为事件，根据分步计数原理，．所以．20．2022年的重庆遇到近61年来的第二高温天气，为了在2023年的夏季降温和冬季供暖时减少能源损耗，拟对某幢建筑物的屋顶和外墙建造隔热层．已知由新材料制作的隔热层能使用20年，每厘米厚的隔热层建造成本为5万元．该建筑物每年的能源消耗费用（单位：万元）与隔热层厚度（单位：）满足关系：，设为隔热层建造费用与20年的能源消耗费用之和．(1)求的表达式；(2)隔热层修建多厚时，总费用达到最小，并求最小值．【答案】(1)(2)当隔热层修建5cm厚时，总费用最小，最小值为55万元 【分析】（1）根据题意可直接得到函数的解析式；（2）由（1）可得解析式，求导可得，从而得到其极小值，即为最小值．【详解】（1）每年能源消耗费用为，建造费用为，∴．（2），令得或（舍）．∴当时，，当时，．∴在上单调递减，在上单调递增．∴当时，取得极小值，也是最小值，∴当隔热层修建5cm厚时，总费用最小，最小值为55万元．21．已知函数．(1)当时，求函数的极值；(2)讨论的单调性．【答案】(1)当时，取得极大值3，当时，取得极小值(2)答案见解析 【分析】（1）求出，根据的正负即可求出函数的极值；（2）求出，令，得出或，分类讨论的取值范围即可．【详解】（1）当时，，则，令，得或，当时，，单调递增，当时，，单调递减，当时，，单调递增，所以当时，取得极大值，当时，取得极小值，（2），令，则或，当时，，，，，则在和上单调递增，在上单调递减；当时，，，，，则在和上单调递增，在上单调递减；当时，，，则在上单调递增；综上所述，当时，在和上单调递增，在上单调递减；当时，在和上单调递增，在上单调递减；当时，在上单调递增．22．已知函数.(1)若在上单调递减，求实数的取值范围；(2)若时，存在两个极值点、，证明：.【答案】(1)(2)证明见解析 【分析】（1）由题意可得在上恒成立，转化为在上恒成立，构造函数，利用导数可求出的取值范围，即可得出实数的取值范围；（2）由（1）知：、满足，，不妨设，则，则，所以只需证成立，构造函数，利用导数证明出对任意的恒成立即可.【详解】（1）解：因为，则，因为函数在上单调递减，则对任意的，，即，可得，设，则，当时，，所以，单调递增，则，故，即实数的取值范围是．（2）证明：由（1）知：、满足，则，不妨设，则．则，则要证，即证，即证，也即证成立．设函数，则，所以，在单调递减，又．故当时，，所以，，即.【点睛】方法点睛：利用导数证明不等式问题，方法如下：（1）直接构造函数法：证明不等式（或）转化为证明（或），进而构造辅助函数；（2）适当放缩构造法：一是根据已知条件适当放缩；二是利用常见放缩结论；（3）构造“形似”函数，稍作变形再构造，对原不等式同解变形，根据相似结构构造辅助函数.