八年级数学上册专题11.16 三角形几何模型-A字型（专项练习）-2022-2023学年八年级数学上册基础知识专项讲练（人教版）

专题11.16 三角形几何模型-A字型（专项练习）

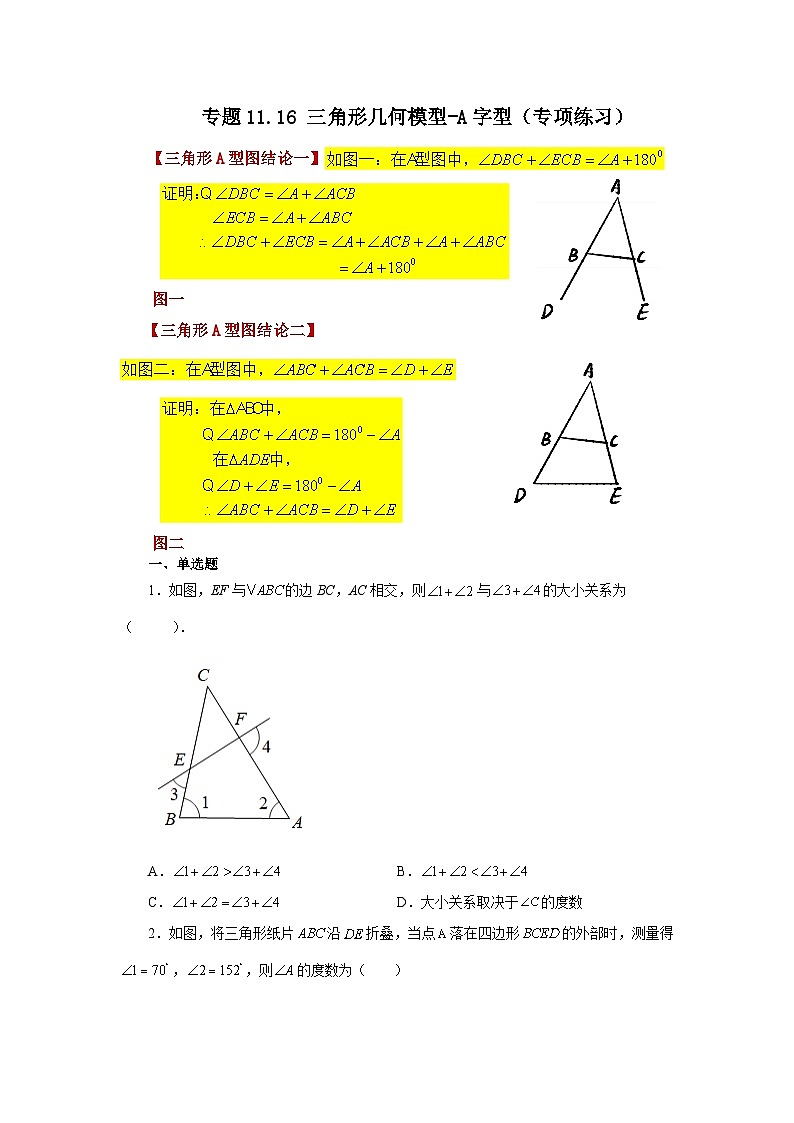
【三角形A型图结论一】

图一            

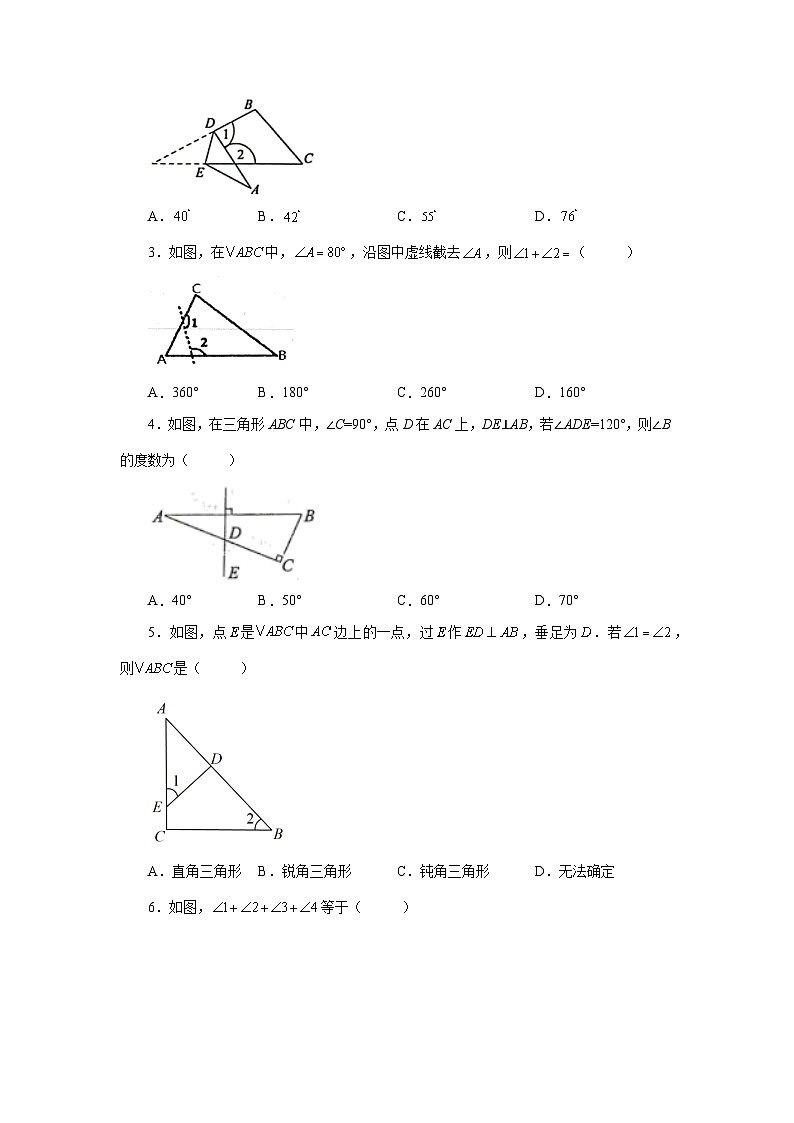
【三角形A型图结论二】                   

图二

一、单选题

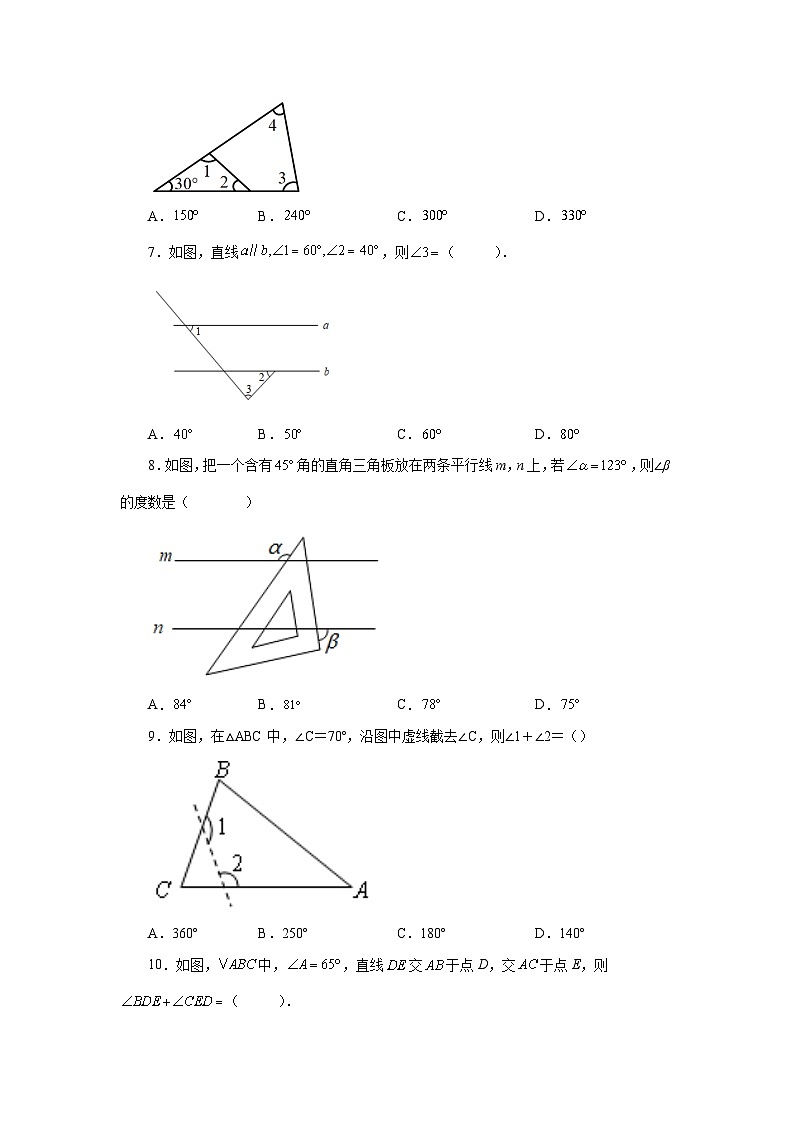
1．如图，EF与的边BC，AC相交，则与的大小关系为（       ）．

A． B．

C． D．大小关系取决于的度数

2．如图，将三角形纸片沿折叠，当点落在四边形的外部时，测量得，，则的度数为（     ）

A． B． C． D．

3．如图，在中，，沿图中虚线截去，则（       ）

A．360° B．180° C．260° D．160°

4．如图，在三角形ABC中，∠C=90°，点D在AC上，DE⊥AB，若∠ADE=120°，则∠B的度数为（       ）

A．40° B．50° C．60° D．70°

5．如图，点是中边上的一点，过作，垂足为．若，则是（       ）

A．直角三角形 B．锐角三角形 C．钝角三角形 D．无法确定

6．如图，等于（       ）

A． B． C． D．

7．如图，直线，则（       ）．

A． B． C． D．

8．如图，把一个含有角的直角三角板放在两条平行线m，n上，若，则∠β的度数是（          ）

A． B． C． D．

9．如图，在△ABC中，∠C＝70º，沿图中虚线截去∠C，则∠1＋∠2＝（）

A．360º B．250º C．180º D．140º

10．如图，中，，直线交于点D，交于点E，则（       ）．

A． B． C． D．

11．如图，对于△ABC，若存在点D，E，F分别在BC，AC，AB上，使得，，，则称△DEF为△ABC的“反射三角形”．下列关于“反射三角形”的说法中，正确的是（       ）

A．若△DEF为△ABC的“反射三角形”，且，则

B．若△DEF为△ABC的“反射三角形”，则

C．直角三角形的“反射三角形”必为直角三角形

D．若△ABC的反射三角形存在，则△ABC必为锐角三角形

12．如图，已知，，，则的度数为（       ）

A．105° B．110° C．115° D．125°

13．如图，直线，在中，，AC⊥b，垂足为A，则图中与∠1互余的角有（       ）

A．2个 B．3个 C．4个 D．5个

二、填空题

14．如图，已知点D、E在的边上，，则是__________三角形．

15．如图，将直角三角形纸片ABC进行折叠，使直角顶点A落在斜边BC上的点E处，并使折痕经过点C，得到折痕CD．若∠CDE=70°，则∠B=______°．

16．如图，△ABC中，∠A＝60°，∠B＝40°，DE∥BC，则∠AED的度数是______．

17．如图是某建筑工地上的人字架，若，那么的度数为_________．

18．如图，将三角形纸片ABC沿EF折叠，使得A点落在BC上点D处，连接DE，DF，．设，，则α与β之间的数量关系是________．

19．如图，在中，，三角形两外角的角平分线交于点E，则________．

三、解答题

20．如图所示，的两边上各有一点，连接，求证．

参考答案

1．C

【分析】

根据对顶角相等和三角形的内角和定理即可得结论．

解：∵∠3=∠CEF,∠4=∠CFE

∴∠CEF+∠CFE+∠C=∠3+∠4+∠C=180°

又∵∠1+∠2+∠C=180°

∴

故选：C

【点拨】本题主要考查对顶角的性质和三角形的内角和定理，掌握对顶角的性质和三角形的内角和定理是解题的关键．

2．B

【分析】

根据折叠∠A′=∠A，根据邻补角性质求出∠A′DA，再根据三角形外角性质即可求解．

解：根据折叠可知∠A′=∠A，

∵∠1=70°，

∴∠A′DA=180°-∠1=110°，

∴根据三角形外角∠A′=∠2-∠A′DA=152°-110°=42°，

∴∠A=42°．

故选B．

【点拨】本题考查折叠性质，邻补角性质，三角形外角性质，掌握折叠性质，邻补角性质，三角形外角性质是解题关键．

3．C

【分析】

先利用三角形内角与外角的关系，得出∠1+∠2=∠A+（∠A+∠3+∠4），再根据三角形内角和定理即可得出结果．

解：如图，

∵∠1、∠2是三角形的外角，

∴∠1=∠4+∠A，∠2=∠3+∠A，

即∠1+∠2=∠A+（∠A+∠3+∠4）=80°+180°=260°．

故选：C．

【点拨】此题主要考查了三角形内角和定理及外角的性质，三角形内角和是180°；三角形的任一外角等于和它不相邻的两个内角之和．

4．C

【分析】

先根据三角形外角的性质求出∠A=30°，再根据三角形内角和定理求出∠B的度数．

解：如图，

∵DE⊥AB，

∴∠DFA=90°，

∵∠ADE=120°，

∴∠A=∠AED-∠DFA =120°-90°=30°，

∵∠C=90°，

∴∠B=90°-∠A =90°-30°=60°，

故选 C．

【点拨】本题主要考查三角形外角的性质、垂直的定义，熟练掌握三角形外角的性质是解决本题的关键．

5．A

【分析】

先求解再证明可得从而可得结论.

解：

是直角三角形．

故选A

【点拨】本题考查的是垂直的定义，三角形的内角和定理的应用，掌握“三角形的内角和定理”是解本题的关键．

6．C

【分析】

在两个三角形中，分别利用三角形内角和定理，即可得到答案．

解：由图可知，在△ABC中∠1+∠2=180°-30°=150°，

在△AED中∠3+∠4=180°-30°=150°，

所以∠1+∠2+∠3+∠4 =300°

故选C

【点拨】本题考查三角形的内角和定理，三角形内角和定理：三角形三个内角的和等于180°．

7．D

【分析】

根据平行线的性质求出∠4，根据三角形内角和定理计算即可．

解：

∵a∥b，

∴∠4=∠1=60°，

∴∠3=180°-∠4-∠2=80°

故选：D．

【点拨】本题考查的是平行线的性质、三角形内角和定理，掌握两直线平行，同位角相等是解题的关键．

8．C

【分析】

如图设∠1、∠2、∠3、∠4，根据平行线的性质、三角形内角和以及对顶角相等即可求解．

解：如图，设∠1、∠2、∠3、∠4，

∵∠α=123°，，

∴∠α=∠4=123°，

∴∠1=180°-123°=57°，

∵三角板的顶角∠2=45°，

∴∠3=180°-∠1-∠2=180°-57°-45°=78°，

∵∠β=∠3，

∴∠β=78°，

故选：C．

【点拨】本题考查了两线平行同位角相等、对顶角相等和三角形内角和为180°等知识，充分平行线的性质以及三角形内角和是解答本题的关键．

9．B

【分析】

根据三角形内角和定理得出∠A+∠B=110°，进而利用四边形内角和定理得出答案．

解：∵△ABC中，∠C=70°，

∴∠A+∠B=180°-∠C =110°，

∴∠1+∠2=360°-110°=250°，

故选B．

【点拨】本题主要考查了多边形内角和定理，根据题意得出∠A+∠B的度数是解题关键.

10．D

【分析】

根据三角形内角和定理求出，根据平角的概念计算即可．

解：，

，

，

故选：D．

【点拨】本题考查的是三角形内角和定理的应用，掌握三角形内角和等于是解题的关键．

11．D

【分析】

根据反射三角形的定义及三角形内角和定理求出∠1=∠2=∠C，∠3=∠4=∠B，∠5=∠6=∠A再逐个判断．

解：如下图所示：

设∠1=∠2=x，

则∠3=∠4=180°-∠A-x，∠5=∠6=180°-∠B-x，

∵∠4+∠5+∠C=180°，

∴(180°-∠A-x)+(180°-∠B-x)+∠C=180°，且∠A+∠B+∠C=180°，

∴x=∠C，即∠1=∠2=∠C，

∴∠3=∠4=180°-∠A-x=180°-∠A-∠C=∠B，∠5=∠6=180°-∠B-x=180°-∠B-∠C=∠A；

∵∠1+∠2+∠EDF=180°，

∴2∠C+∠EDF=180°；

下面对选项逐个判断：

选项A：，，若，则，得不到，故选项A错误；

选项B：若△DEF为△ABC的“反射三角形”，则，故选项B错误；

选项C：在直角三角形中，不存在反射三角形，理由如下：

当∠C=90°时，∠EDF+2∠C=180°，得到∠EDF=0°，这显然与题意矛盾，故选项C错误；

选项D：在钝角三角形中，也不存在反射三角形，理由如下：

当∠C＞90°时，∠EDF+2∠C=180°，得到∠EDF<0°，这显然与题意矛盾，

故若△ABC的反射三角形存在，则△ABC必为锐角三角形，

故选：D．

【点拨】本题借助三角形内角和定理考查了“反射三角形”，属于新定义题型，解题的关键是读懂题意，合理使用三角形内角和定理．

12．A

【分析】

由两直线平行内错角相等解得，再由三角形外角的性质解答即可．

解：

故选：A．

【点拨】本题考查平行线的性质、三角形外角的性质等知识，是重要考点，掌握相关知识是解题关键．

13．C

【分析】

首先在△ABC中由∠C=90°得∠1+∠B=90°，根据直线AC⊥b得∠1+∠2=90°，直线得∠2=∠∠3，∠2=∠4，等量代换∠1+∠3=90°，∠1+∠4=90°，最后综合所得与∠1互余的角有4个分别为：∠2、∠3、∠4、∠B ．

解：如图所示，

∠C=90°，

∠1+∠B=90°，

∠1与∠B互余;

又a//b，

∠2=∠3，∠2=∠4， .

又AC⊥b，

∠1+∠2=90°，

∠1+∠3=90°，∠1+∠4=90°，

∠1与∠2互余，∠1与∠3互余，

综合所述与∠1互余的角有∠2、∠3、 ∠4、∠B，

故选：C．

【点拨】本题综合考查了平行线的性质、垂直的定义、对顶角的性质、余角与补角的定义等相关知识点，掌握平行线的性质解题的关键．

14．直角

【分析】

由两直线平行，同位角相等得到，再由三角形内角和定理解题．

解：∵，

∴，

∵，

∴．

∴是直角三角形，

故答案为：直角．

【点拨】本题考查平行线的性质、三角形内角和定理等知识，是基础考点，掌握相关知识是解题关键．

15．50

【分析】

根据折叠的性质求得∠CDE=∠CDA=70°，得到∠BDE=40°，再利用余角的性质即可求解．

解：根据折叠的性质得：∠CDE=∠CDA=70°，∠CED=∠A=90°，

∴∠BDE=180°-70°-70°=40°，∠BED=180°-90°=90°，

∴∠B=180°-90°-40°=50°，

故答案为：50．

【点拨】本题考查翻折变换，三角形内角和定理等知识，关键是根据翻折前后对应角相等，利用三角形内角和定理求解即可．

16．80°

【分析】

根据三角形内角和定理可得∠C=80°，根据平行线的性质即可得答案．

解：∵∠A＝60°，∠B＝40°，

∴∠C＝180°﹣∠A﹣∠B=80°，

∵DE∥BC，

∴∠AED＝∠C＝80°，

故答案为：80°

【点拨】本题考查三角形内角和定理及平行线的性质，任意三角形的内角和等于180°；两直线平行，同位角相等；熟练掌握相关性质及定理是解题关键．

17．

【分析】

根据平角的定义求出，再利用三角形的外角的性质即可解决问题．

解：如图

，，

，

，

，

故答案为：．

【点拨】本题考查三角形外角的性质、平角的性质等知识，解题的关键是熟练掌握基本知识，属于中考基础题．

18．

【分析】

由折叠的性质可知：，再利用三角形内角和定理及角之间的关系证明，，即可找出α与β之间的数量关系．

解：由折叠的性质可知：，

∵，

∴，

∴，

∵，

，

∴，

∴，

故答案为：．

【点拨】本题考查折叠的性质，三角形内角和定理，解题的关键是根据折叠的性质求出，根据角之间的关系求出，．

19．61°

【分析】

先根据三角形的内角和定理和平角定义求得∠DAC+∠ACF的度数，再根据角平分线的定义求得∠EAC+∠ECA的度数，即可解答．

解：∵∠B+∠BAC+∠BCA=180°，∠B=58°，

∴∠BAC+∠BCA=180°﹣∠B=180°﹣58°=122°，

∵∠BAC+∠DAC=180°，∠BCA+∠ACF=180°，

∴∠DAC+∠ACF=360°﹣（∠BAC+∠BCA）=360°﹣122°=238°，

∵AE平分∠DAC，CE平分∠ACF，

∴∠EAC=∠DAC，∠ECA=∠ACF，

∴∠EAC+∠ECA =（∠DAC+∠ACF）=119°，

∵∠EAC+∠ECA+∠AEC=180°，

∴∠AEC=180°﹣（∠EAC+∠ECA）=180°﹣119°=61°，

故答案为：61°．

【点拨】本题考查三角形的内角和定理、角平分线的定义、平角定义，熟练掌握三角形的内角和定理和角平分线的定义是解答的关键．

20．见分析

【分析】

根据三角形的外角等于与它不相邻的两个内角的和证明即可．

解：和是的外角，

．

又，

．

【点拨】本题主要考查三角形外角的性质，熟知三角形的外角等于与它不相邻的两个内角的和是解题的关键．