八年级数学上册专题11.19 三角形几何模型-燕尾角（专项练习）-2022-2023学年八年级数学上册基础知识专项讲练（人教版）

这是一份八年级数学上册专题11.19 三角形几何模型-燕尾角（专项练习）-2022-2023学年八年级数学上册基础知识专项讲练（人教版），共20页。
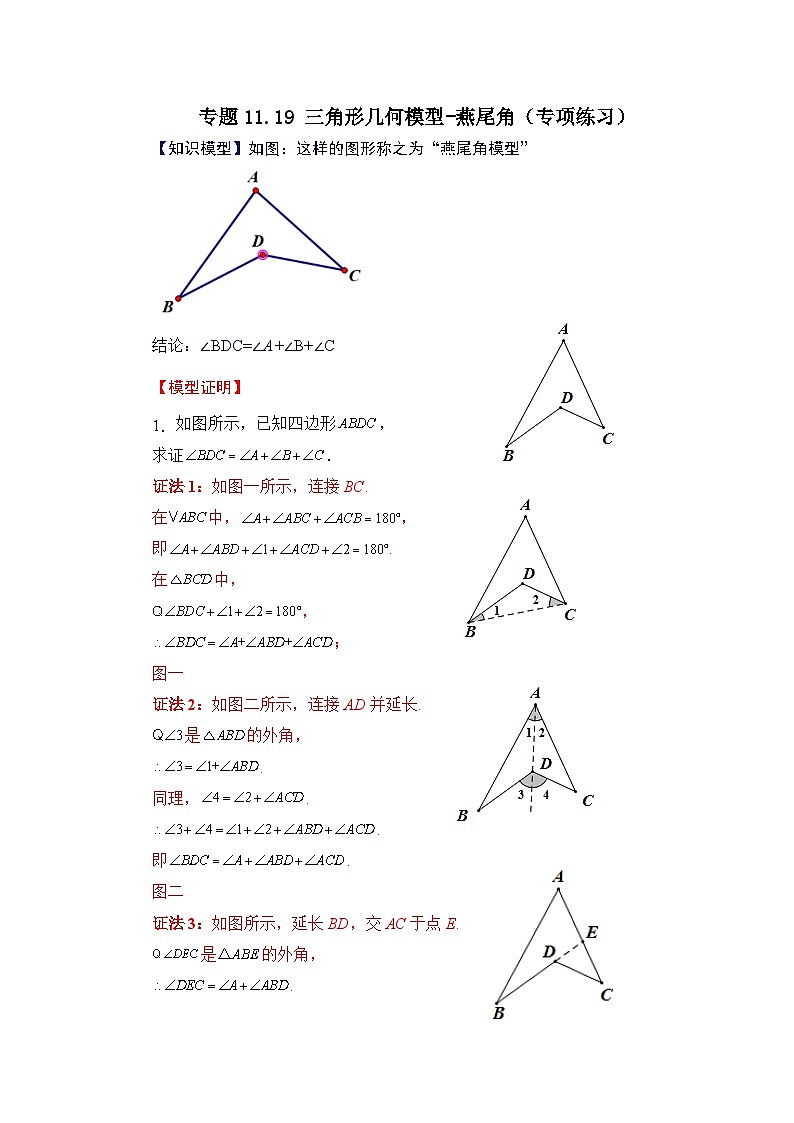
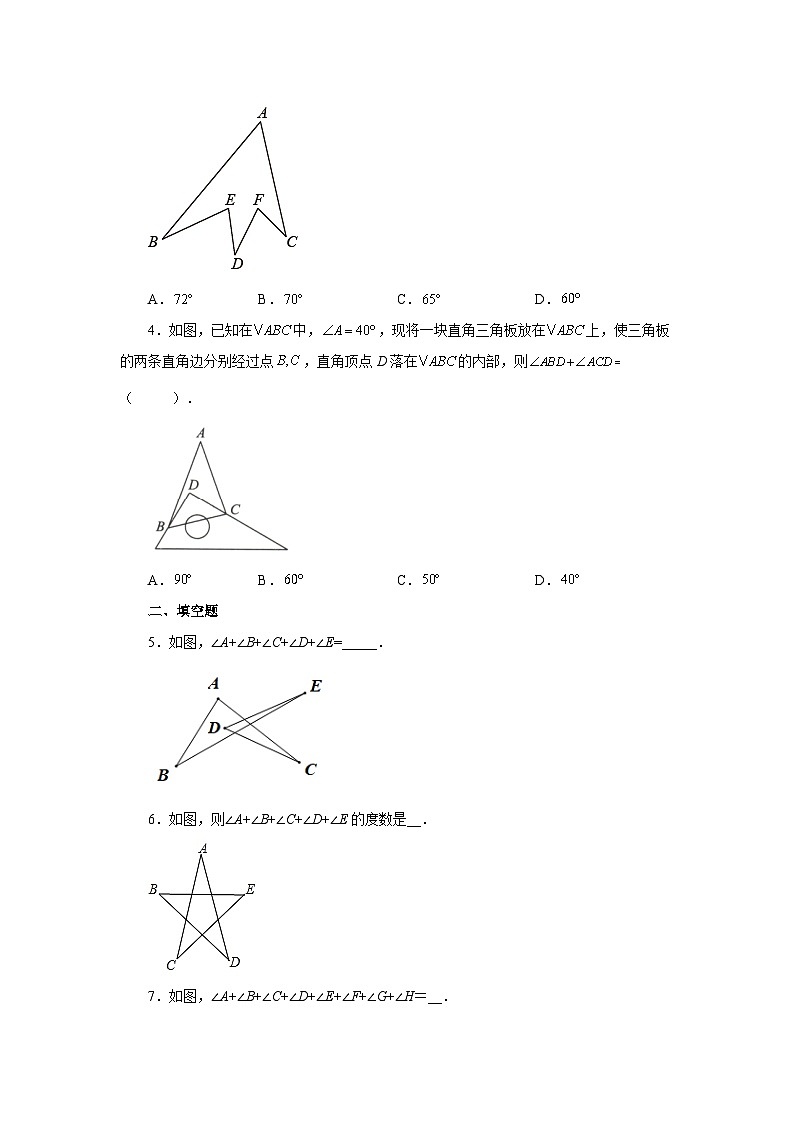
专题11.19 三角形几何模型-燕尾角（专项练习）【知识模型】如图：这样的图形称之为“燕尾角模型”结论：∠BDC=∠A+∠B+∠C【模型证明】1．如图所示，已知四边形，求证．证法1：如图一所示，连接BC. 在中，，即.在中，，；图一证法2：如图二所示，连接AD并延长.             是的外角，.同理，..即.                        图二证法3：如图所示，延长BD，交AC于点E.是的外角，.是的外角，..                             图三【点拨】本题考查了三角形的外角性质：解题的关键是知道三角形的任一外角等于与之不相邻的两内角的和．也考查了三角形内角和定理．一、单选题1．如图所示，∠A+∠B+∠C+∠D+∠E的结果为（       ）A．90° B．360° C．180° D．无法确定2．如图，已知BE，CF分别为△ABC的两条高，BE和CF相交于点H，若∠BAC=50°，则∠BHC为（　　）A．115° B．120° C．125° D．130°3．在社会实践手工课上，小茗同学设计了一个形状如图所示的零件，如果，，那么的度数是（       ）．A． B． C． D．4．如图，已知在中，，现将一块直角三角板放在上，使三角板的两条直角边分别经过点，直角顶点D落在的内部，则（       ）．A． B． C． D．二、填空题5．如图，∠A+∠B+∠C+∠D+∠E=_____．6．如图，则∠A+∠B+∠C+∠D+∠E的度数是__．7．如图，∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H＝__．8．如图，∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H＝__．9．如图，若，则____________．10．如图，在中，，，平分，平分，则______.三、解答题11．如图(1)所示的图形，像我们常见的学习用品——圆规．我们不妨把这样图形叫做“规形图”，那么在这一个简单的图形中，到底隐藏了哪些数学知识呢？下面就请你发挥你的聪明才智，解决以下问题：（1）观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系，并说明理由；（2）请你直接利用以上结论，解决以下三个问题：①如图(2)，把一块三角尺XYZ放置在△ABC上，使三角尺的两条直角边XY、图(1)XZ恰好经过点B、C，若∠A=50°，则∠ABX+∠ACX =__________°；②如图(3)DC平分∠ADB,EC平分∠AEB,若∠DAE=50°，∠DBE=130°，求∠DCE的度数；（写出解答过程）③如图（4），∠ABD，∠ACD的10等分线相交于点G1、G2、G9，若∠BDC=140°，∠BG1C=77°，则∠A的度数=__________°．    12．如图，已知分别交的边、于、，交的延长线于，，，，求的度数.        13．如图，是的平分线，CH是的平分线，与CH交于点，若，，求的度数.     14．如图，、分别平分和，若，，求的度数.  15．如图，是上一点，是上一点，，相交于点，，，，求的度数. 16．模型规律：如图1，延长交于点D，则．因为凹四边形形似箭头，其四角具有“”这个规律，所以我们把这个模型叫做“箭头四角形”．模型应用（1）直接应用：①如图2，，则__________；②如图3，__________；（2）拓展应用：①如图4，、的2等分线（即角平分线）、交于点，已知，，则__________；②如图5，、分别为、的10等分线．它们的交点从上到下依次为、、、…、．已知，，则__________；③如图6，、的角平分线、交于点D，已知，则__________；④如图7，、的角平分线、交于点D，则、、之同的数量关系为__________．         17．如图，中，（1）若、的三等分线交于点、，请用表示、；（2）若、的等分线交于点、（、依次从下到上），请用表示，.   参考答案1．C解：如图，连接BC，∵∠D+∠E+∠DOE=∠BOC+∠OCB+∠BOC=180°，∠DOE=∠BOC，∴∠D+∠E=∠OBC+∠OCB，又∵∠A+∠ABO+∠ACO+∠OBC+∠OCB=180°，∴∠A+∠ABO+∠ACO+∠D+∠E=180°.故选C.2．D解：∵BE为△ABC的高，∠BAC=50°，∴∠ABE=90°-50°=40°，∵CF为△ABC的高，∴∠BFC=90°，∴∠BHC=∠ABE+∠BFC=40°+90°=130°．故选D．3．A【分析】延长BE交CF的延长线于O，连接AO，根据三角形内角和定理求出再利用邻补角的性质求出，再根据四边形的内角和求出，根据邻补角的性质即可求出的度数．解：延长BE交CF的延长线于O，连接AO，如图，∵ ∴ 同理得∵ ∴ ∵ ∴ ∴ ∴,故选：A．【点拨】本题考查三角形内角和定理，多边形内角和，三角形的外角的性质，邻补角的性质，解题关键是会添加辅助线，将已知条件联系起来进行求解．三角形外角的性质：三角形的一个外角等于与它不相邻的两个内角的和；邻补角性质：邻补角互补；多边形内角和：．4．C【分析】由三角形内角和定理可得∠ABC+∠ACB+∠A=180°，即∠ABC+∠ACB=180-∠A=140°，再说明∠DBC+∠DCB=90°，进而完成解答．解：∵在△ABC中，∠A=40°∴∠ABC+∠ACB=180-∠A=140°∵在△DBC中，∠BDC=90°∴∠DBC+∠DCB=180°-90°=90°∴40°-90°=50°故选C．【点拨】本题主要考查三角形内角和定理，灵活运用三角形内角和定理成为解答本题的关键．5．##180度【分析】利用三角形的外角的性质将五个角转化为三角形的三个角的和即可．解：如图：利用三角形的外角的性质得：，，所以，故答案为：．【点拨】本题考查了多边形的内角与外角及三角形的内角和与外角和的知识，解题的关键是能够正确的将几个角转化为三个角，难度不大．6．180°【分析】由三角形的一个外角等于与它不相邻的两个内角的和，得∠4＝∠A＋∠2，∠2＝∠D＋∠C，进而利用三角形的内角和定理求解．解：如图可知：∵∠4是三角形的外角，∴∠4＝∠A＋∠2，同理∠2也是三角形的外角，∴∠2＝∠D＋∠C，在△BEG中，∵∠B＋∠E＋∠4＝180°，∴∠B＋∠E＋∠A＋∠D＋∠C＝180°．故答案为：180°．【点拨】本题考查三角形外角的性质及三角形的内角和定理，解答的关键是沟通外角和内角的关系．7．720°【分析】根据三角形的外角等于与它不相邻的两个内角的和，可得∠2与∠H、∠G的关系，∠1与∠2、∠D的关系，根据多边形的内角和公式，可得答案．解：如图：由三角形的外角等于与它不相邻的两个内角的和，得∠2＝∠H＋∠G，∠1＝∠2＋∠D，∠1＝∠H＋∠G＋∠D，∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠G＋∠H＝∠A＋∠B＋∠C＋∠E＋∠F＋∠H＋∠G＋∠D＝180°×（6－2）＝270°．故答案为：720°．【点拨】本题考查了多边形的内角与外角，先求出∠1＝∠H＋∠G＋∠D，再求出多边形的内角和．8．360°【分析】连接CF，根据三角形的外角得到由三角形外角的性质可得：∠2＝∠G＋∠H，∠3＝∠A＋∠B，∠1＝∠D＋∠E＝∠4＋∠5，根据四边形的内角和为360°，可得：∠2＋∠3＋∠GFE＋∠4＋∠5＋∠DCB＝360°即∠G＋∠H＋∠A＋∠B＋∠GFE＋∠D＋∠E＋∠DCB＝360°．解：如图，连接FC，由三角形外角的性质可得：∠2＝∠G＋∠H，∠3＝∠A＋∠B，∠1＝∠D＋∠E＝∠4＋∠5，根据四边形的内角和为360°，可得：∠2＋∠3＋∠GFE＋∠4＋∠5＋∠DCB＝360°即∠G＋∠H＋∠A＋∠B＋∠GFE＋∠D＋∠E＋∠DCB＝360°，故答案为360°．【点拨】本题考查了三角形的内角与外角，解决本题的关键是熟记三角形的外角的性质．9．230°【分析】根据三角形外角的性质，得到∠EOC=∠E+∠2=115°，∠2=∠D+∠C，∠EOC=∠1+∠F=115°，∠1=∠A+∠B，即可得到结论．解：如图∵∠EOC=∠E+∠2=115°，∠2=∠D+∠C， ∴∠E+∠D+∠C=115°， ∵∠EOC=∠1+∠F=115°，∠1=∠A+∠B， ∴∠A+∠B+∠F=115°，∴∠A+∠B+∠C+∠D+∠E+∠F=230°， 故答案为：230°．【点拨】本题主要考查三角形内角和定理和三角形外角的性质，解决本题的关键是要熟练掌握三角形外角性质．10．【分析】先根据角平分线的性质求出的度数，再利用三角形内角和定理即可求解.解：∵平分，平分，∴，∴.【点拨】本题考查了角平分线的性质及三角形内角和定理.熟练掌握三角形内角和定理是解题的关键.11．（1）∠BDC=∠A+∠B+∠C，详见分析；（2）①40；②∠DCE=90°；③70【分析】（1）根据题意观察图形连接AD并延长至点F，根据一个三角形的外角等于与它不相邻的两个内角的和可证∠BDC=∠BDF+∠CDF；（2）①由（1）的结论可得∠ABX+∠ACX+∠A=∠BXC，然后把∠A=50°，∠BXC=90°代入上式即可得到∠ABX+∠ACX的值；②结合图形可得∠DBE=∠DAE+∠ADB+∠AEB，代入∠DAE=50°，∠DBE=130°即可得到∠ADB+∠AEB的值，再利用上面得出的结论可知∠DCE=（∠ADB+∠AEB）+∠A，易得答案．③由②方法，进而可得答案．解：（1）连接AD并延长至点F，由外角定理可得∠BDF＝∠BAD+∠B，∠CDF＝∠C+∠CAD；∵∠BDC＝∠BDF+∠CDF，∴∠BDC＝∠BAD+∠B+∠C+∠CAD.∵∠BAC＝∠BAD+∠CAD；∴∠BDC＝∠BAC +∠B+∠C；（2）①由（1）的结论易得：∠ABX+∠ACX+∠A＝∠BXC，∵∠A＝50°，∠BXC＝90°，∴∠ABX+∠ACX＝90°﹣50°＝40°．故答案是：40；②由（1）的结论易得∠DBE＝∠DAE +∠ADB+∠AEB，∠DCE＝∠ADC＋∠AEC＋∠A∵∠DAE=50°，∠DBE=130°，∴∠ADB+∠AEB＝80°；∵DC平分∠ADB,EC平分∠AEB, ∴∠ADC=∠ADB,∠AEC=∠AEB∴∠DCE＝(∠ADB+∠AEB)+∠A=40°+50°=90°；③由②知，∠BG1C＝(∠ABD+∠ACD)+ ∠A，∵∠BG1C＝77°，∴设∠A为x°，∵∠ABD+∠ACD＝140°﹣x°，∴(140﹣x)＋x＝77，∴14﹣x+x＝77，∴x＝70，∴∠A为70°．故答案是：70．【点拨】本题考查三角形外角的性质，三角形的内角和定理的应用，能求出∠BDC=∠A+∠B+∠C是解答的关键，注意：三角形的内角和等于180°，三角形的一个外角等于和它不相邻的两个内角的和．12．.【分析】根据三角形的内角和定理即可求解解：在中，=--，∴∠DEC=【点拨】本题主要考查三角形内角和定理和外角的性质，掌握三角形内角和为180°及三角形的一个外角等于不相邻两个内角的和是解题的关键．13．.【分析】根据三角形的外角的性质得出燕尾角的基本图形的结论得出∠BDC、∠BOC，在根据角平分线的性质即可得出解：由燕尾角的基本图形与结论可得，①②是的平分线，是的平分线，．①-②得，．【点拨】本题考查了三角形的内角和定理，角平分线的定义．注意利用“8字形”的对应角相等求出角的关系是解题的关键，要注意整体思想的利用．14．.【分析】根据三角形内角和定理用∠B、∠M表示出∠BAM-∠BCM，再用∠B、∠M表示出∠MAD-∠MCD，再根据角平分线的定义可得∠BAM-∠BCM=∠MAD-∠MCD，然后求出∠M与∠B、∠D关系，代入数据进行计算即可得解；解：根据三角形内角和定理，∠B+∠BAM=∠M+∠BCM，∴∠BAM-∠BCM=∠M-∠B，同理，∠MAD-∠MCD=∠D-∠M，∵AM、CM分别平分∠BAD和∠BCD，∴∠BAM=∠MAD，∠BCM=∠MCD，∴∠M-∠B=∠D-∠M，∴∠M=（∠B+∠D）=（42°+54°）=48°；【点拨】本题考查了三角形的内角和定理，角平分线的定义．注意利用“8字形”的对应角相等求出角的关系是解题的关键，要注意整体思想的利用．15．.【分析】根据三角形的外角性质先求出的度数，再利用三角形内角和定理即可注出的度数.解：在△ADC中，，在在△BDF中，.【点拨】本题考查了三角形内角和定理及三角形外角的性质.熟练找出三角形内角与外角的关系是解题的关键.16．（1）①110；②260；（2）①85；②110；③142；④∠B-∠C+2∠D=0【分析】（1）①根据题干中的等式直接计算即可；②同理可得∠A+∠B+∠C+∠D+∠E+∠F=∠BOC+∠DOE，代入计算即可；（2）①同理可得∠BO1C=∠BOC-∠OBO1-∠OCO1，代入计算可得；②同理可得∠BO7C=∠BOC-（∠BOC-∠A），代入计算即可；③利用∠ADB=180°-（∠ABD+∠BAD）=180°-（∠BOC-∠C）计算可得；④根据两个凹四边形ABOD和ABOC得到两个等式，联立可得结论．解：（1）①∠BOC=∠A+∠B+∠C=60°+20°+30°=110°；②∠A+∠B+∠C+∠D+∠E+∠F=∠BOC+∠DOE=2×130°=260°；（2）①∠BO1C=∠BOC-∠OBO1-∠OCO1=∠BOC-（∠ABO+∠ACO）=∠BOC-（∠BOC-∠A）=∠BOC-（120°-50°）=120°-35°=85°；②∠BO7C=∠BOC-（∠BOC-∠A）=120°-（120°-50°）=120°-10°=110°；③∠ADB=180°-（∠ABD+∠BAD）=180°-（∠BOC-∠C）=180°-（120°-44°）=142°；④∠BOD=∠BOC=∠B+∠D+∠BAC，∠BOC=∠B+∠C+∠BAC，联立得：∠B-∠C+2∠D=0．【点拨】本题主要考查了新定义—箭头四角形，利用了三角形外角的性质，还考查了角平分线的定义，图形类规律，解题的关键是理解箭头四角形，并能熟练运用其性质．17．（1），；（2），.【分析】（1）根据三角形内角和可得，再根据、的三等分线交于点、，可得然后根据三角形内角和定理即可用含表示、；（2）根据（1）中所体现的规律解答即可.解：（1）∵，∴，∵、的三等分线交于点、，∴∴，；（2）由（1）可知，.【点拨】本题考查了三角形内角和定理及角的n等分线的性质.熟练应用三角形内角和定理求角的度数是解题的关键.