人教版七年级上册4.3.1 角综合训练题

这是一份人教版七年级上册4.3.1 角综合训练题，共23页。

线段与角的计算．
（1）如图1，已知点为上一点，，，若、分别为、的中点，求的长．
（2）已知：如图2，被分成，平分，平分，且，求的度数．
【解答】解：（1），，
，
．
，分别为，的中点，
，，
；
（2）设，，，则，
平分，平分，
，，
，
又，
，
，
．
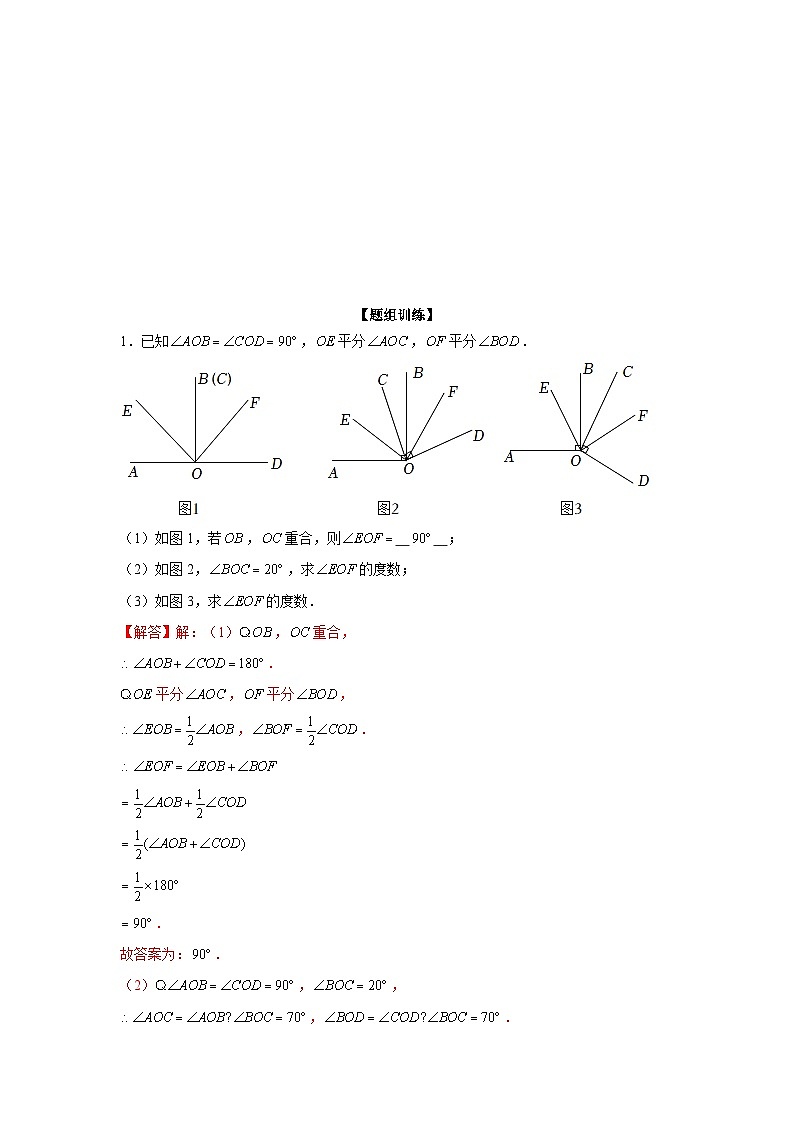
【题组训练】
1．已知，平分，平分．
（1）如图1，若，重合，则 ；
（2）如图2，，求的度数；
（3）如图3，求的度数．
【解答】解：（1），重合，
．
平分，平分，
，．
．
故答案为：．
（2），，
，．
平分，平分，
，．
．
（3）设．
，，
，．
平分，平分，
，．
．
2．点在直线上，在直线的同侧，作射线，，平分．
（1）如图1，若，，直接写出的度数为 ，的度数为 ；
（2）如图2，若，求的度数；
（3）若和互为余角且，，，平分，试画出图形探究；与之间的数量关系，并说明理由．
【解答】解：（1），，
；
，
平分，
，
；
故答案为：，；
（2），
设，则，
，
平分，
，
；
（3）或，
理由：如图3，和互为余角，
设，则，
，
平分，
，
，
，平分，
，
，
；
如图4，和互为余角，
设，则，
，
平分，
，
，
，平分，
，
，
；
综上所述，与之间的数量关系为或．
3．如图，点是线段的中点，是上一点，．
（1）若为的中点，且，求的长；
（2）若，求的长．
【解答】解：（1）点是线段的中点，
，
设，
，
，
为的中点，
，
；
（2），
设，则，
点是线段的中点，
，
，
，
，
．
4．如图，线段，是线段上一点，，是的中点，是的中点．
（1） 8 ， ；
（2）求线段的长；
（3）求线段的长．
【解答】解：（1）线段，，
，
是的中点，
．
故答案为：8，10；
（2）由（1）得，，
．
答：的长度是；
（3）是的中点，
，
．
答：线段的长度是．
5．如图，已知线段和的公共部分，线段、的中点、之间距离是，求，的长．
【解答】解：设，则，，．
点、点分别为、的中点，
，．
．
，
，
解得：．
，．
6．如图，已知、在线段上．
（1）图中共有 6 条线段；
（2）若．
①比较线段的长短： （填：“”、“ ”或“” ；
②若，，是的中点，是的中点，求的长度．
【解答】解：（1）以为端点的线段有、、共3条；以为端点的线段有、共2条；以为端点的线段为，有1条，故共有线段的条数为：，
故答案为：6；
（2）①，，且
故答案为：；
（2）①若，则，
即．
故答案为：；
②，，
，
是的中点，是的中点，
，，
，
．
7．已知：如图，是直线上的一点，，平分．
（1）若，求的度数；
（2）若，求的度数（用含的代数式表示）．
【解答】解：（1）平分，，
，
．
（2）平分，若，
，
，
，
．
8．如图所示，，分别平分和．如果，，求的度数．
【解答】解：如图所示：
，
，，
，
又平分，
，
又，
，
又平分，
，
又，
．
9．如图，已知，平分，且，求的度数．
【解答】解：如图所示：
，，
平分
，
又，
．
10．如图，点是直线上一点，，在直线的异侧，且，平分，平分．
（1）若，求和的度数；
（2）设，用含的式子表示．
【解答】解：（1）平分，，
，
，
，
，
，
平分，
．
（2），平分，
，
，
，
，
平分，
．
11．已知，如图，，是的平分线，是的平分线，且．
（1）求的度数；
（2）求的度数．
【解答】解：（1）设，．
则．
是的平分线，
，
，
，
，
解得，，
是的平分线，
，
．
（2）
12．如图，点、、在同一条直线上．
（1）比大，求与的度数；
（2）在（1）的条件下，若与互余，求的度数；
（3）在（1）（2）的条件下，若平分，求的度数．
【解答】解：（1）比大，
，
又点、、在同一条直线上．
，
，
，
；
（2）与互余，
，
；
（3）平分，
得，
，
．
13．如图，点，，在一条直线上，，平分．
（1）若，求的余角的度数；
（2）若，求的度数．
【解答】解：（1），，
，
的余角，
的余角的度数是；
（2），，
，
点，，在一条直线上，
，
，
平分，
，
，
的度数为．
14．如图，已知线段，点、都是线段上的点，点是的中点．
（1）若，求线段的长；
（2）在（1）的条件下，若，且点是线段的中点，求线段的长．
【解答】解：（1），，
，
点是的中点，
；
（2），
，，
点是线段的中点，
，
，，
．
15．如图，已知点是线段上一点，点是线段的中点，若，．
（1）求线段的长；
（2）若点是直线上一点，且，求线段的长．
【解答】解：（1）点是线段的中点，，
，
；
（2）①当点在点的右侧时，如图：
，，
，
；
②当点在点的左侧时，如图：
，，
，
；
综上，的长为或．
16．如图，已知线段，在线段上有四个点，，，，在的右侧，且，，，求线段的长．
【解答】解：，，
，，，
，
，
，
，
，
．
17．如图，已知线段长，点、、、顺次在上，且，是的中点，，求的长．
【解答】解：设，则，
，
是的中点，
，
，
，
，
，
．
18．如图，线段，点是线段的中点，点是线段的中点．
（1）求线段的长；
（2）若在线段上有一点，，求的长．
【解答】解：（1），是的中点，
，
是的中点，
，
；
（2），，
，
当在的左边时，；
当在的右边时，．
的长为4或8．
19．如图，已知在线段上两点、，点是的中点，，．求线段的长．
【解答】解：，
设，，
，
为线段的中点，
，
，
，
，
．
20．如图，点是线段的中点，点、点分别是线段、上的点，且，，若，求线段的长．
【解答】解：，
，
而是线段的中点，
，
，
又，
，
故线段的长为．
21．如图，已知，，点是的中点，点是的中点，求线段的长．
【解答】解：，，
，
为中点，
，
为中点，
，
．
22．如图所示，，，是的中点，求的长．
【解答】解：，，
，
点是的中点，
，
．
即的长是．
23．如图，已知线段，，点是的中点．
（1）求线段的长；
（2）在上取一点，使得，求线段的长．
【解答】解：（1）线段，，
．
又点是的中点．
，即线段的长度是4．
（2），，
．
又点是的中点，，
，
，
即的长度是9．
24．（1）如图①，线段，点为线段的中点，求线段的长；
（2）如图②，在（1）的条件下，点、分别是、的中点，求线段的长．
【解答】解：（1）线段，点为线段的中点，
．
（2）、分别是线段、的中点，
，，
线段，
．
25．如图，已知，是内的一条射线，且．
（1）求的度数；
（2）过点作射线，若，求的度数．
【解答】解：（1），，
；
（2），
，
当在内时，
，
当在外时，
．
故的度数为或．
26．如图所示，是的平分线，是的平分线，，，求的度数．
【解答】解：如图所示：
，
，，
，
是的平分线，
，
同理可得：
又
．
27．如图，为直线上一点，，平分．
（1）若，则 ；
（2）若是的5倍，求度数．
【解答】解：（1），，
．
．
平分．
．
故答案为：．
（2）设，
则．
．
．
平分，
．
，
即
，
．
28．如图，将绕点逆时针旋转角，得到．
（1）若，且，求的度数．
（2）若，且，求角的度数．
【解答】解：（1）将绕点逆时针旋转角，得到，
．
．
即．
，，
．
．
．
（2）由（1）知：．
，
设，则．
，
．
．
．
将绕点逆时针旋转角，得到，
．
29．如图，已知，为内部的一条射线，．若平分，为内部的一条射线，，求的度数．
【解答】解：，平分，
，
，，
，，
．
30．如图，已知直线，是直线上一点．是的平分线，是的平分线．．
（1）求的度数；
（2）求的度数．
【解答】解：（1）是的平分线，
，
又，
，
，
；
（2）是的平分线．，
，
，
．