专题02 与三角形有关的角（七大类型）（题型专练）-2023-2024学年八年级数学上册《知识解读•题型专练》（人教版）

这是一份专题02 与三角形有关的角（七大类型）（题型专练）-2023-2024学年八年级数学上册《知识解读•题型专练》（人教版），文件包含专题02与三角形有关的角七大类型题型专练原卷版docx、专题02与三角形有关的角七大类型题型专练解析版docx等2份试卷配套教学资源，其中试卷共27页， 欢迎下载使用。
专题02 与三角形有关的角（七大类型）

【题型 1 三角形的内角和定理】
【题型 2直角三角形的内角有关运算】
【题型3三角形中有关高、中线与角平分线综合运算】
【题型4三角形外角性质】
【题型5三角形双内角平分线的有关运算】
【题型6三角形双外角平分线的有关运算】
【题型7 三角形内、外角平分线的有关运算】

【题型 1 三角形的内角和定理】
1．（2022春•叠彩区校级期中）在△ABC中，∠A＝70°，∠B＝20°，那么这个三角形是（　　）
A．锐角三角形 B．直角三角形 C．钝角三角形 D．无法确定
【答案】B
【解答】解：在△ABC中，∠A＝70°，∠B＝20°，
∴∠C＝180°﹣∠A﹣∠B＝90°，
∴△ABC是直角三角形．
故选：B．
2．（2022春•南开区期中）在△ABC中，已知∠A＝4∠B＝104°，则∠C的度数是（　　）
A．50° B．45° C．40° D．35°
【答案】A
【解答】解：∵4∠B＝104°，
∴∠B＝26°，
∴∠C＝180°﹣∠A﹣∠B＝180°﹣104°﹣26°＝50°．
故选：A．
3．（2022春•平房区期中）如图，∠D＝80°，∠C＝30°，∠A＝75°，则∠B＝（　　）

A．35° B．30° C．25° D．20°
【答案】A
【解答】解：∵∠A+∠B+∠AOB＝∠COD+∠C+∠D，∠AOB＝∠COD，
∴∠A+∠B＝∠C+∠D．
∵∠D＝80°，∠C＝30°，∠A＝75°，
∴75°+∠B＝30°+80°．
∴∠B＝35°．
故选：A．
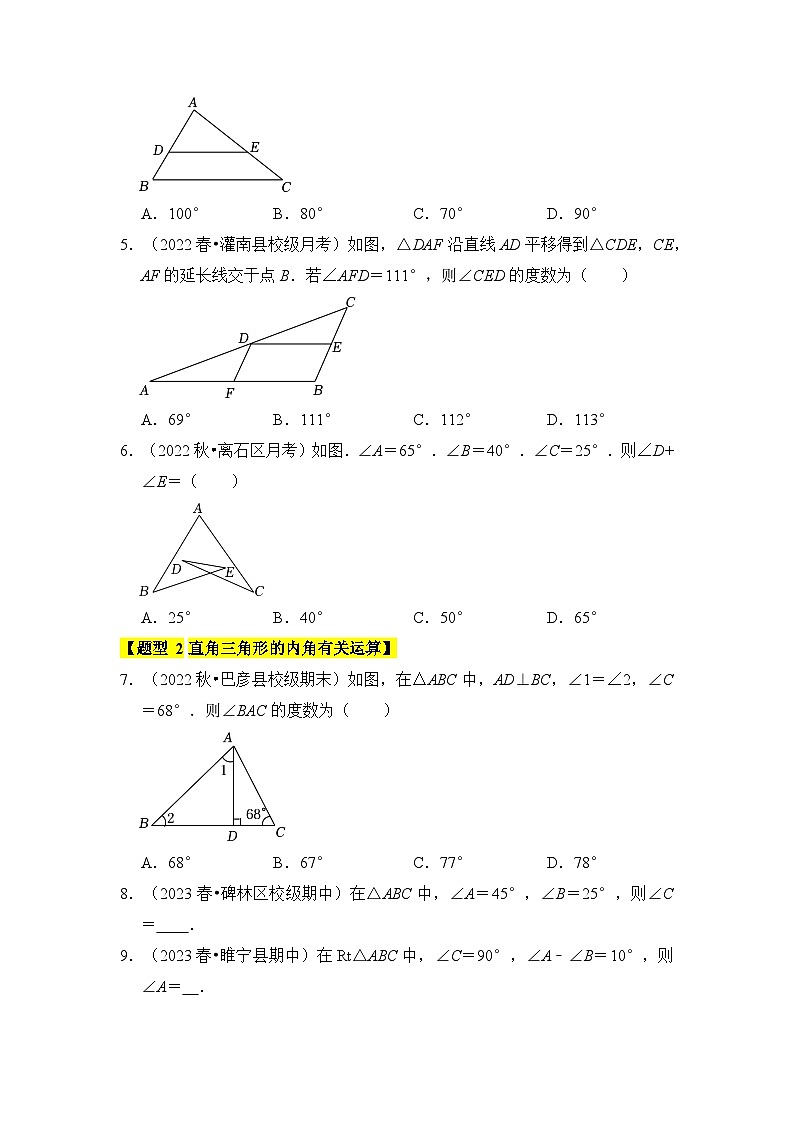
4．（2022春•南海区校级期中）如图，已知D、E在△ABC的边上，DE∥BC，∠B＝60°，∠AED＝40°，则∠A的度数为（　　）

A．100° B．80° C．70° D．90°
【答案】B
【解答】解：∵DE∥BC，∠AED＝40°，
∴∠C＝∠AED＝40°，
∵∠B＝60°，
∴∠A＝180°﹣∠C﹣∠B＝180°﹣40°﹣60°＝80°．
故答案为：B．
5．（2022春•灌南县校级月考）如图，△DAF沿直线AD平移得到△CDE，CE，AF的延长线交于点B．若∠AFD＝111°，则∠CED的度数为（　　）

A．69° B．111° C．112° D．113°
【答案】B
【解答】解：∵△DAF沿直线AD平移得到△CDE，
∴∠CED＝∠AFD＝111°，
故选：B．
6．（2022秋•离石区月考）如图．∠A＝65°．∠B＝40°．∠C＝25°．则∠D+∠E＝（　　）

A．25° B．40° C．50° D．65°
【答案】C
【解答】解：连接BC，如右图所示，
∵∠A＝65°，∠ABE＝40°，∠ACD＝25°，
∴∠1+∠2＝180°﹣∠A﹣∠ABE﹣∠ACD＝180°﹣65°﹣40°﹣25°＝50°，
∵∠D+∠E＝∠1+∠2，
∴∠D+∠E＝50°．
故选：C．


【题型 2直角三角形的内角有关运算】
7．（2022秋•巴彦县校级期末）如图，在△ABC中，AD⊥BC，∠1＝∠2，∠C＝68°．则∠BAC的度数为（　　）

A．68° B．67° C．77° D．78°
【答案】B
【解答】解：∵AD⊥BC，∠1＝∠2，∠C＝68°，
∴∠2＝∠1＝45°，
∵∠BAC＝180°﹣∠2﹣∠C＝180°﹣45°﹣68°＝67°，
故选：B．
8．（2023春•碑林区校级期中）在△ABC中，∠A＝45°，∠B＝25°，则∠C＝　110°　．
【答案】110°．
【解答】解：∠C＝180°﹣45°﹣25°＝110°，
故答案为：110°．
9．（2023春•睢宁县期中）在Rt△ABC中，∠C＝90°，∠A﹣∠B＝10°，则∠A＝　50°　．
【答案】50°．
【解答】解：∵三角形的内角和等于180度，∠C＝90°，
∴∠A+∠B＝90°，即∠B＝90°﹣∠A，
∵∠A﹣∠B＝10°，
∴∠A﹣（90°﹣∠A）＝10°．
∴∠A＝50°．
故答案为：50°．
【题型3三角形中有关高、中线与角平分线综合运算】
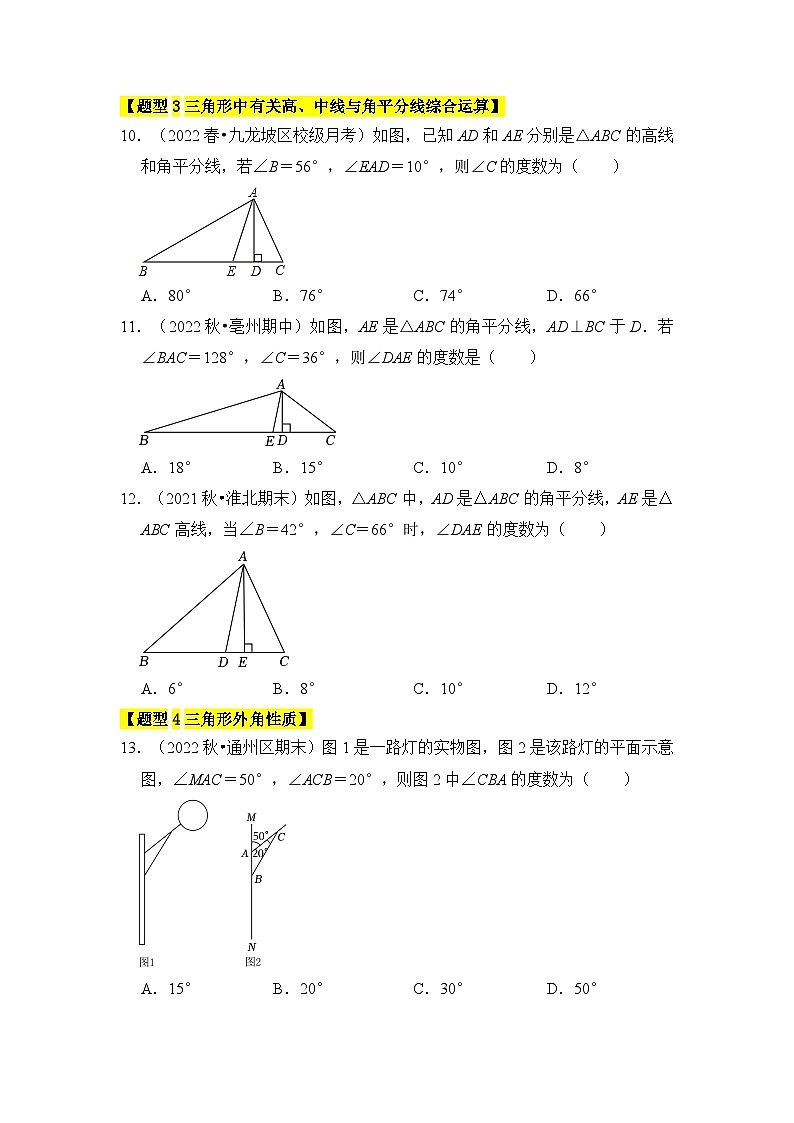
10．（2022春•九龙坡区校级月考）如图，已知AD和AE分别是△ABC的高线和角平分线，若∠B＝56°，∠EAD＝10°，则∠C的度数为（　　）

A．80° B．76° C．74° D．66°
【答案】B
【解答】解：∵AD是高，∠B＝56°，
∴∠BAD＝90°﹣56°＝34°，
∵∠DAE＝10°，
∴∠BAE＝∠BAD﹣∠EAD＝34°﹣10°＝24°，
∵AE是角平分线，
∴∠BAC＝2∠BAE＝48°，
∵∠CAD＝∠CAE﹣∠EAD＝24°﹣10°＝14°
∴∠C＝180°﹣90°﹣14°＝76°．
故选：B．
11．（2022秋•亳州期中）如图，AE是△ABC的角平分线，AD⊥BC于D．若∠BAC＝128°，∠C＝36°，则∠DAE的度数是（　　）

A．18° B．15° C．10° D．8°
【答案】C
【解答】解：∵AD⊥BC，∠C＝36°，
∴∠CAD＝90°﹣36°＝54°，
∵AE是△ABC的角平分线，∠BAC＝128°，
∴∠CAE＝∠BAC＝×128°＝64°，
∴∠DAE＝∠CAE﹣∠CAD＝64°﹣54°＝10°．
故选：C．
12．（2021秋•淮北期末）如图，△ABC中，AD是△ABC的角平分线，AE是△ABC高线，当∠B＝42°，∠C＝66°时，∠DAE的度数为（　　）

A．6° B．8° C．10° D．12°
【答案】D
【解答】解：在△ABC中，∠B＝42°，∠C＝66°，
∴∠BAC＝180°﹣∠B﹣∠C＝180°﹣42°﹣66°＝72°，
∵AD平分∠BAC，
∴∠CAD＝∠BAC＝×72°＝36°．
∵AE⊥BC，
∴∠AEC＝90°，
∴∠CAE＝90°﹣∠C＝90°﹣66°＝24°，
∴∠DAE＝∠CAD﹣∠CAE＝36°﹣24°＝12°．
故选：D．
【题型4三角形外角性质】
13．（2022秋•通州区期末）图1是一路灯的实物图，图2是该路灯的平面示意图，∠MAC＝50°，∠ACB＝20°，则图2中∠CBA的度数为（　　）

A．15° B．20° C．30° D．50°
【答案】C
【解答】解：∵∠MAC＝50°，∠ACB＝20°，∠MAC是△ABC的外角，
∴∠CBA＝∠MAC﹣∠ACB＝30°．
故选：C．
14．（2022春•吴江区期中）把一块直尺与一块三角板如图放置，若∠2＝134°，则∠1的度数为（　　）

A．34° B．44° C．54° D．64°
【答案】B
【解答】解：如图：

由题意得：AD∥BC，
∴∠2＝∠AGH＝134°，
∵∠AGH是△EFG的一个外角，
∴∠AGH＝∠1+∠E，
∴∠1＝∠AGH﹣∠E＝44°，
故选：B．
15．（2022秋•宁津县校级月考）将一副直角三角板如图放置，使两直角边重合，则∠α的度数为（　　）

A．75° B．105° C．135° D．165°
【答案】D
【解答】解：∠AOC＝∠DAB﹣∠C＝15°，
∴∠α＝180°﹣15°＝165°，
故选：D．

16．（2022秋•铁东区期中）如图，CE是△ABC的外角∠ACD的平分线，若∠B＝45°，∠ACE＝65°，则∠A的度数是 　　．

【答案】85°．
【解答】解：∵∠ACE＝65°，CE是△ABC的外角∠ACD的平分线，
∴∠ACD＝2∠ACE＝130°，
∵∠ACD＝∠A+∠B，∠B＝45°，
∴∠A＝∠ACD﹣∠B＝85°，
故答案为：85°．
17．（2022秋•海淀区校级期中）将一副三角板按如图所示的位置摆放，则∠1的度数为（　　）

A．75° B．95° C．105° D．115°
【答案】C
【解答】解：如图所示：

根据题意，得∠B＝45°，∠A＝60°，∠ADE＝90°，
∴∠ADB＝90°，
∴∠BCD＝∠ACF＝45°，
∴∠1＝∠A+∠ACF＝60°+45°＝105°，
故选：C．
18．（2022•平谷区二模）如图，直线AB∥CD，连接BC，点E是BC上一点，∠A＝15°，∠C＝27°，则∠AEC的大小为（　　）

A．27° B．42° C．45° D．70°
【答案】B
【解答】解：∵AB∥CD，∠C＝27°，
∴∠ABE＝∠C＝27°，
∵∠A＝15°，
∴∠AEC＝∠A+∠ABE＝42°，
故选：B．

【题型5三角形双内角平分线的有关运算】
19．（2021秋•肥城市期末）如图，在△ABC中，点D是∠ABC和∠ACB角平分线的交点，若∠BDC＝110°，那么∠A的度数为（　　）

A．40° B．50° C．60° D．70°
【答案】A
【解答】解：∵∠BDC＝110°，
∴∠DBC+∠DCB＝70°，
∵点D是∠ABC和∠ACB角平分线的交点，
∴∠ABC+∠ACB＝2（∠DBC+∠DCB）＝140°，
∴∠A＝180°﹣140°＝40°，
故选：A．
20．（2022秋•巴东县期中）如图，∠A＝40°，∠ABD＝∠ACD＝20°，则∠BDC的度数为（　　）

A．100° B．110° C．90° D．80°
【答案】D
【解答】解：由题意得：∠A+∠CBA+∠ACB＝180°，
∠BDC+∠DBC+∠DCB＝180°，
∵∠A＝40°，
∴∠CBA+∠ACB＝140°，
∴∠CBD+∠ABD+∠ACD+∠DCB＝140°，
∵∠ABD＝∠ACD＝20°，
∴∠CBD+∠DCB＝100°，
∴∠BDC＝180°﹣（∠DBC+∠DCB）＝80°，
故选：D．
21．（2022春•天宁区校级期中）如图△ABC中，∠1＝∠2，∠ABC＝80°，则∠BDC的度数是（　　）

A．110° B．100° C．120° D．130°
【答案】B
【解答】解：∵∠ABC＝80°，
∴∠DBC＝∠ABC﹣∠1，
∵∠1＝∠2，
∴∠BDC＝180°﹣∠DBC﹣∠2＝180°﹣（80°﹣∠1）﹣∠2＝100°
故选：B．
22．（2022秋•乳山市期中）如图，将三角板DEF的直角放置在△ABC内，恰好三角板的两条直角边分别经过点B，C．若∠A＝55°，则∠ABD+∠ACD＝（　　）

A．35° B．45° C．55° D．60°
【答案】A
【解答】解：在△ABC中，∵∠A＝55°，
∴∠ABC+∠ACB＝180°﹣55°＝125°，
在△DBC中，∵∠BDC＝90°，
∴∠DBC+∠DCB＝180°﹣90°＝90°，
∴∠ABD+∠ACD＝125°﹣90°＝35°；
故选：A．
23．（2022秋•柳江区期中）如图，△ABC中，点D，E分别在∠ABC和∠ACB的平分线上，连接BD，DE，EC，若∠D+∠E＝295°，则∠A等于（　　）

A．65° B．60° C．55° D．50°
【答案】D
【解答】解：∵∠D+∠E＝295°，∠D+∠E+∠BCE+∠CBD＝360°，
∴∠BCE+∠CBD＝65°，
∵点D，E分别在∠ABC和∠ACB的平分线上，
∴∠BCE＝∠ACB，∠CBD＝∠ABC，
∴∠ACB+∠ABC＝65°×2＝130°，
∴∠A＝180°﹣130°＝50°，
故选：D．
24．（2022秋•汤阴县期中）如图，在△ABC中，BE平分∠DBC，BD平分∠ABE，CE平分∠BCD，CD平分∠ACE，若∠D＝80°，则∠A等于（　　）

A．30° B．35° C．50° D．85°
【答案】A
【解答】解：∵BE平分∠DBC，BD平分∠ABE，CE平分∠BCD，CD平分∠ACE，
∴∠ABD＝∠DBE＝∠CBE＝∠ABC，∠ACD＝∠DCE＝∠BCE＝∠ACB．
在△BCD中，∠DBC＝∠DBE+∠CBE＝∠ABC，∠DCB＝∠DCE+∠BCE＝∠ACB，∠D＝80°，
∴∠DBC+∠DCB+∠D＝180°，即∠ABC+∠ACB+80°＝180°，
∴∠ABC+∠ACB＝180°﹣80°＝100°，
∴∠ABC+∠ACB＝150°．
在△ABC中，∠A+∠ABC+∠ACB＝180°，
∴∠A＝180°﹣∠ABC﹣∠ACB＝180°﹣（∠ABC+∠ACB）＝180°﹣150°＝30°．
故选：A．
25．（2022秋•阳东区期中）如图，把△ABC纸片沿DE折叠，点A落在四边形DEBC内部A'，当∠A＝30°时，∠1+∠2＝（　　）

A．30° B．40° C．50° D．60°
【答案】D
【解答】解：在△ADE中，∠A＝30°，∠ADE+∠AED＝180°﹣∠A＝180°﹣30°＝150°，
由折叠可知：∠A'DE＝∠ADE，∠A'ED＝∠AED，
∴∠1+∠2＝360°﹣∠A'DE﹣∠ADE﹣∠A'ED﹣∠AED
＝360°﹣2（∠ADE+∠AED）
＝360°﹣2×150°
＝60°．
故选：D．
【题型6三角形双外角平分线的有关运算】
26．（2022秋•江汉区期中）如图，△ABC的外角∠ACE和外角∠CAF的平分线交于点P，已知∠P＝70°，则∠B的度数为（　　）

A．42° B．40° C．38° D．35°
【答案】B
【解答】解：∵AP、CP分别是△ABC的外角∠ACE和外角∠CAF的平分线，
∴，，
∵∠P＝70°，
∴∠PAC+∠PCA＝180°﹣70°＝110°，
∴∠CAF+∠ACE＝2（∠PAC+∠PCA）＝220°，
∵∠FAC+∠BAC＝180°，∠ECA+∠ACB＝180°，
∴∠BAC+∠BCA＝180°+180°﹣（∠FAC+∠ECA）＝140°，
∴∠B＝180°﹣（∠BAC+∠BCA）＝40°，故B正确．
故选：B．
27．（2022秋•义乌市月考）如图，在△ABC中，∠ABC，∠ACB的平分线交于点O，D是∠ACB外角与内角∠ABC平分线交点，E是∠ABC，∠ACB外角平分线交点，若∠BOC＝110°，则∠D＝（　　）度．

A．15° B．20° C．25° D．30°
【答案】B
【解答】解：∵CO平分∠ABC，CD平分∠ABC的外角，
∴∠ACO＝∠ACB，∠ACD＝∠ACF，
∵∠ACB+∠ACF＝180°，
∴∠OCD＝∠ACO+∠ACD＝（∠ACB+∠ACF）＝90°，
∴∠BOC＝∠OCD+∠D，
∴∠D＝110°﹣90°＝20°．
故选：B．
28．（2022秋•长顺县月考）综合与探究：
【情境引入】
（1）如图1，BD，CD分别是△ABC的内角∠ABC，∠ACB的平分线，说明∠D＝90°+∠A的理由．

【深入探究】
（2）①如图2，BD，CD分别是△ABC的两个外角∠EBC，∠FCB的平分线，∠D与∠A之间的等量关系是 　；
②如图3，BD，CD分别是△ABC的一个内角∠ABC和一个外角∠ACE的平分线，BD，CD交于点D，探究∠D与∠A之间的等量关系，并说明理由．

【答案】（1）证明见解析；
（2）①∠D＝90°﹣∠A；
②∠D＝∠A．
【解答】（1）证明：∵BD，CD分别是△ABC的内角∠ABC，∠ACB的平分线，
∴∠1＝∠ABC，∠2＝∠ACB，
∴∠1+∠2+∠D＝180°，∠A+∠ABC+∠ACB＝180°，
∴∠D＝180°﹣∠1﹣∠2
＝180°﹣（∠ABC+∠ACB）
＝180°﹣（180°﹣∠A）
＝90°+∠A；
（2）解：①∠D＝90°﹣∠A，理由如下：
∵BD，CD分别是△ABC的两个外角∠EBC，∠FCB的平分线，
∴∠DBC＝∠EBC＝（∠A+∠ACB），∠DCB＝∠FCB＝（∠A+∠ABC），
∵∠DBC+∠DCB+∠D＝180°，∠A+∠ABC+∠ACB＝180°，
∴∠D＝180°﹣∠DBC﹣∠DCB
＝180°﹣（∠EBC+∠FCB）
＝180°﹣
＝90°﹣∠A，
故答案为：∠D＝90°﹣∠A；
②∠D＝∠A，理由如下：
∵BD，CD分别是△ABC的一个内角∠ABC和一个外角∠ACE的平分线，
∴∠DBC＝∠ABC，∠DCE＝∠ACE，
∵∠ACE＝∠A+∠ABC，∠DCE＝∠D+∠DBC，
∴∠D+∠ABC＝（∠A+∠ABC），
∴∠D＝∠A．

【题型7 三角形内、外角平分线的有关运算】
29．（2022秋•沙洋县期中）如图，BP是△ABC中∠ABC的平分线，CP是∠ACB的外角的平分线，如果∠ABP＝20°，∠ACP＝50°，则∠A+∠P＝（　　）

A．70° B．80° C．90° D．100°
【答案】C
【解答】解：∵BP是△ABC中∠ABC的平分线，CP是∠ACB的外角的平分线，
又∵∠ABP＝20°，∠ACP＝50°，
∴∠ABC＝2∠ABP＝40°，∠ACM＝2∠ACP＝100°，
∴∠A＝∠ACM﹣∠ABC＝60°，
∠ACB＝180°﹣∠ACM＝80°，
∴∠BCP＝∠ACB+∠ACP＝130°，
∵∠PBC＝20°，
∴∠P＝180°﹣∠PBC﹣∠BCP＝30°，
∴∠A+∠P＝90°，
故选：C．
30．（春•温江区校级期中）如图所示，△ABC中，∠A＝m，延长BC到D，∠ABC与∠ACD的角平分线相交于A1点，则∠A1的大小是　　，∠A1BC与∠A1CD的平分线相交于A2点，依此类推，∠A2015BC与∠A2015CD的角平分线相交于A2016点，则∠A2016的大小是　　．

【答案】
【解答】解：∵A1B平分∠ABC，A1C平分∠ACD，
∴∠A1BC＝∠ABC，∠A1CA＝∠ACD，
∵∠A1CD＝∠A1+∠A1BC，
即∠ACD＝∠A1+∠ABC，
∴∠A1＝（∠ACD﹣∠ABC），
∵∠A+∠ABC＝∠ACD，
∴∠A＝∠ACD﹣∠ABC，
∴∠A1＝∠A＝，
同法可得：∠A2＝∠A1＝∠A，
…
以此类推∠A2016＝∠A＝．
故答案为，．

31．（2021春•衡阳县期末）如图①，在△ABC中，∠ABC与∠ACB的平分线相交于点P．
（1）如果∠A＝80°，求∠BPC的度数；
（2）如图②，作△ABC外角∠MBC，∠NCB的角平分线交于点Q，试探索∠Q、∠A之间的数量关系．
（3）如图③，延长线段BP、QC交于点E，△BQE中，存在一个内角等于另一个内角的2倍，求∠A的度数．

【解答】（1）解：∵∠A＝80°．
∴∠ABC+∠ACB＝100°，
∵点P是∠ABC和∠ACB的平分线的交点，
∴∠P＝180°﹣（∠ABC+∠ACB）＝180°﹣×100°＝130°，
（2）∵外角∠MBC，∠NCB的角平分线交于点Q，
∴∠QBC+∠QCB＝（∠MBC+∠NCB）
＝（360°﹣∠ABC﹣∠ACB）
＝（180°+∠A）
＝90°+∠A
∴∠Q＝180°﹣（90°+∠A）＝90°﹣∠A；
（3）延长BC至F，
∵CQ为△ABC的外角∠NCB的角平分线，
∴CE是△ABC的外角∠ACF的平分线，
∴∠ACF＝2∠ECF，
∵BE平分∠ABC，
∴∠ABC＝2∠EBC，
∵∠ECF＝∠EBC+∠E，
∴2∠ECF＝2∠EBC+2∠E，
即∠ACF＝∠ABC+2∠E，
又∵∠ACF＝∠ABC+∠A，
∴∠A＝2∠E，即∠E＝∠A；
∵∠EBQ＝∠EBC+∠CBQ
＝∠ABC+∠MBC
＝（∠ABC+∠A+∠ACB）＝90°．
如果△BQE中，存在一个内角等于另一个内角的2倍，那么分四种情况：
①∠EBQ＝2∠E＝90°，则∠E＝45°，∠A＝2∠E＝90°；
②∠EBQ＝2∠Q＝90°，则∠Q＝45°，∠E＝45°，∠A＝2∠E＝90°；
③∠Q＝2∠E，则90°﹣∠A＝∠A，解得∠A＝60°；
④∠E＝2∠Q，则∠A＝2（90°﹣∠A），解得∠A＝120°．
综上所述，∠A的度数是90°或60°或120°．