冀教版九年级下册第30章 二次函数30.4 二次函数的应用课时练习

这是一份冀教版九年级下册第30章 二次函数30.4 二次函数的应用课时练习，共9页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
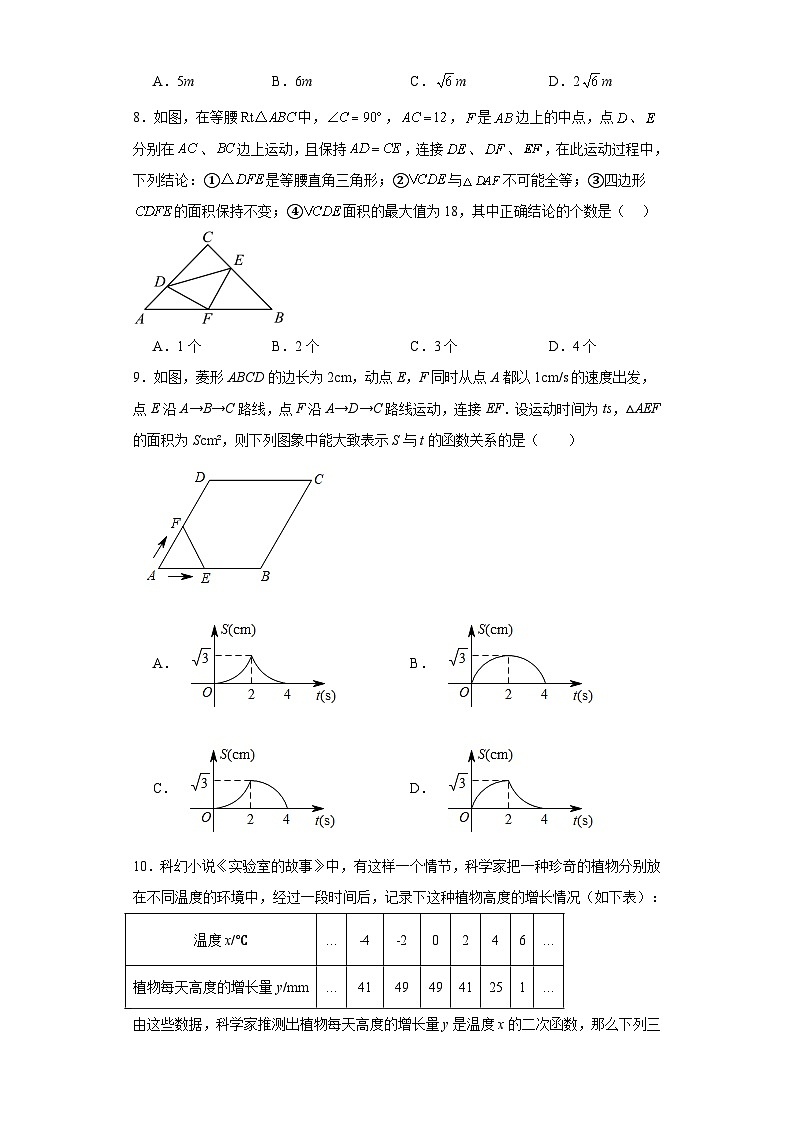
30.4二次函数的应用基础练习-冀教版数学九年级下册学校:___________姓名：___________班级：___________考号：___________ 一、单选题1．滑雪者从山坡上滑下，其滑行距离S（单位：m）与滑行时间t（单位：s）之间的关系可以近似地用二次函数刻画，其图象如图所示，根据图象，当滑行时间为4s时，滑行距离为（　　）A．40m B．48m C．56m D．72m2．如图1，E为矩形ABCD边AD上一点，点P从点B沿折线BE﹣ED﹣DC运动到点C时停止，点Q从点B沿BC运动到点C时停止，它们运动的速度都是1cm/s．若P，Q同时开始运动，设运动时间为t（s），△BPQ的面积为y（cm2）．已知y与t的函数图象如图2，则下列结论错误的是【 】A．AE=6cm B．C．当0＜t≤10时， D．当t=12s时，△PBQ是等腰三角形3．将抛物线y=2x2+4x-5的图象向左平移2个单位，再向上平移1个单位，所得抛物线解析式是（　　）A．y=2（x+1）2-7 B．y=2（x+1）2-6 C．y=2（x+3）2-6 D．y=2（x-1）2-64．图（1）是一个横断面为抛物线形状的拱桥，当水面在l时，拱顶（拱桥洞的最高点）离水面，水面宽，如图（2）建立平面直角坐标系，则抛物线的关系式是（　　）  A．  B．  C．  D． 5．如图①，在等边三角形中，点为边上的任意一点，且交于点，设线段的长度为的长度为若与的函数关系的大致图象如图②所示，则等边三角形的面积为(　　)A． B． C． D．6．如图，在△ABO中，∠B=90º ，OB=3,OA=5，以AO上一点P为圆心，PO长为半径的圆恰好与AB相切于点C，则下列结论正确的是（　　）．A．⊙P 的半径为B．经过A，O，B三点的抛物线的函数表达式是C．点（3，2）在经过A，O，B三点的抛物线上D．经过A，O，C三点的抛物线的函数表达式是7．如图，有一座抛物线形拱桥，当水位线在AB位置时，拱顶（即抛物线的顶点）离水面2m，水面宽为4m，水面下降1m后，水面宽为（    ）A．5m B．6m C．m D．2m8．如图，在等腰中，，，是边上的中点，点、分别在、边上运动，且保持，连接、、，在此运动过程中，下列结论：①是等腰直角三角形；②与不可能全等；③四边形的面积保持不变；④面积的最大值为18，其中正确结论的个数是（    ）A．1个 B．2个 C．3个 D．4个9．如图，菱形ABCD的边长为2cm，动点E，F同时从点A都以1cm/s的速度出发，点E沿A→B→C路线，点F沿A→D→C路线运动，连接EF．设运动时间为ts，△AEF的面积为Scm²，则下列图象中能大致表示S与t的函数关系的是（　　）A． B．C． D．10．科幻小说《实验室的故事》中，有这样一个情节，科学家把一种珍奇的植物分别放在不同温度的环境中，经过一段时间后，记录下这种植物高度的增长情况（如下表）：温度x/℃…﹣4﹣20246…植物每天高度的增长量y/mm…41494941251…由这些数据，科学家推测出植物每天高度的增长量y是温度x的二次函数，那么下列三个结论：①该植物在0℃时，每天高度的增长量最大；②该植物在﹣6℃时，每天高度的增长量能保持在25mm左右；③该植物与大多数植物不同，6℃以上的环境下高度几乎不增长.上述结论中，所有正确结论的序号是A．①②③ B．①③ C．①② D．②③ 二、填空题11．如图，是一个横断面为抛物线形状的拱桥，当水面宽4m时，拱顶（拱桥洞的最高点）离水面2m，当水面上升1m时，水面的宽为      ．12．如图，有一块四边形的铁板余料ABCD．经测量，AB＝50cm，BC=108cm，CD＝60cm，tanB＝tanC＝，M、N边BC上，顶点P在CD上，顶点Q在AB上，且面积最大的矩形PQMN面积为  cm2．13．如图，把一块等腰直角三角板△ABC，∠C=90°，BC=5，AC=5．现将△ABC沿CB方向平移到△A′B′C′的位置，若平移距离为x（0≤x≤5），△ABC与△A′B′C′的重叠部分的面积y，则y=          （用含x的代数式表示y）．14．某超市购进一批单价为8元的生活用品，如果按每件9元出售，那么每天可销售20件．经调查发现，这种生活用品的销售单价每提高1元，其销售量相应减少4件，那么将销售价定为          元时，才能使每天所获销售利润最大．15．去年下半年以来，我市遭遇连续干旱，各地河流的水位连续下降，小明仔细观察并测量自家门口的抛物线型拱桥的水位高度与水面宽度，发现两周来每周水位下降的高度相同，而第一周水面宽度增加1米，而第二周水面宽度增加0.8米，小明刚开始观察时，他家门口抛物线型拱桥的水面宽为       米．16．抛物线与x轴交于点A、B，与y轴交于点C，则△ABC的面积为             ．17．矩形的周长为20cm，当矩形的长为     cm时，面积有最大值是     cm2．18．如图，△ABC是直角三角形，∠A＝90°，AB＝8 cm，AC＝6 cm，点P从点A出发，沿AB方向以2 cm/s的速度向点B运动；同时点Q从点A出发，沿AC方向以1 cm/s的速度向点C运动，其中一个动点到达终点，另一个动点也停止运动，则△APQ的最大面积是        ．19．如图，y1反映某公司的销售收入与销量的关系，y2反映了该公司产品的销售成本与销量的关系，当公司赢利时销量必须               20．某座石拱桥的桥拱近似抛物线形，以拱顶O为原点，建立如图所示的平面直角坐标系，则其解析式为，当水面宽度是10米时，水面到拱顶的高度是      米． 三、解答题21．已知某商品的进价为每件40元.现在的售价是每件60元，每星期可卖出300件.市场调查反映：如调整价格，每涨价一元，每星期要少卖出10件；每降价一元，每星期可多卖出20件.如何定价才能使利润最大?利润最大是多少?22．已知抛物线=（≠0）与轴交于A､B两点,与轴交于C点,其对称轴为=1,且A（-1,0）､C（0,2）.（1）直接写出该抛物线的解析式;（2）P是对称轴上一点,△PAC的周长存在最大值还是最小值?请求出取得最值（最大值或最小值）时点P的坐标;（3）设对称轴与轴交于点H,点D为线段CH上的一动点（不与点C､H重合）.点P是（2）中所求的点.过点D作DE∥PC交轴于点E.连接PD､PE.若CD的长为,△PDE的面积为S,求S与之间的函数关系式,试说明S是否存在最值,若存在,请求出最值,并写出S取得的最值及此时的值;若不存在,请说明理由.23．如图，在等腰△ABC中，AB=AC=4cm，∠B=30°，点P从点B出发，以cm/s的速度沿BC方向运动到点C停止，同时点Q从点B出发，以1cm/s的速度沿BA-AC方向运动到点C停止，若△BPQ的面积为y（cm2），运动时间为x（s），求在这一运动过程中y与x之间函数关系式.  24．如图1，已知点О在四边形ABCD的边AB上，且OA＝OB＝OC＝OD＝3，OC平分∠BOD，与BD交于点G，AC分别与BD、OD交于点E、F．（1）求证：OC∥AD；（2）如图2，若DE＝DF，求的值；（3）当四边形ABCD的周长取最大值时，求的值．
参考答案：1．B2．D3．C4．C5．B6．D7．D8．C9．C10．D11．12．1944 13．x2﹣5x+．14．1115．3.1．16．617．     5     2518．16 cm219．大于40件20．1.2521．定价为65元时可获得最大利润为6250元.22．(1) =-++2;(2) P（1,）;(3)略.23．y=．24．（1）略；（2）；（3）