初中数学华师大版九年级下册2. 二次函数y=ax2+bx+c的图象与性质一等奖课件ppt

这是一份初中数学华师大版九年级下册2. 二次函数y=ax2+bx+c的图象与性质一等奖课件ppt，共18页。PPT课件主要包含了开口方向，对称轴，x-2，所以函数即为，描点连线，开口向下，顶点坐标是20，yax2+bx+c，二次函数的顶点式，二次函数的一般表达式等内容，欢迎下载使用。
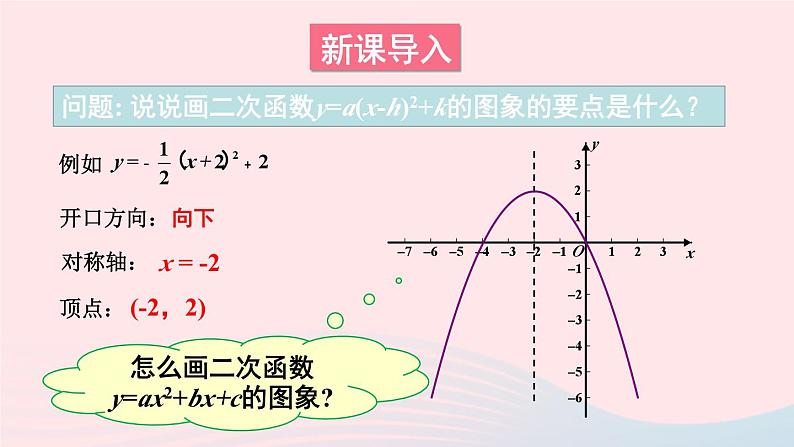
问题: 说说画二次函数y=a(x-h)2+k的图象的要点是什么？
怎么画二次函数y=ax2+bx+c的图象?
画出函数 的图象并说明这个函数具有哪些性质？
因为 ，
因此这个函数的图象开口向下，对称轴为直线 x = 1，顶点坐标为（1，-2）.
先配方，将函数关系式化为 y=a(x-h)2+k的形式.
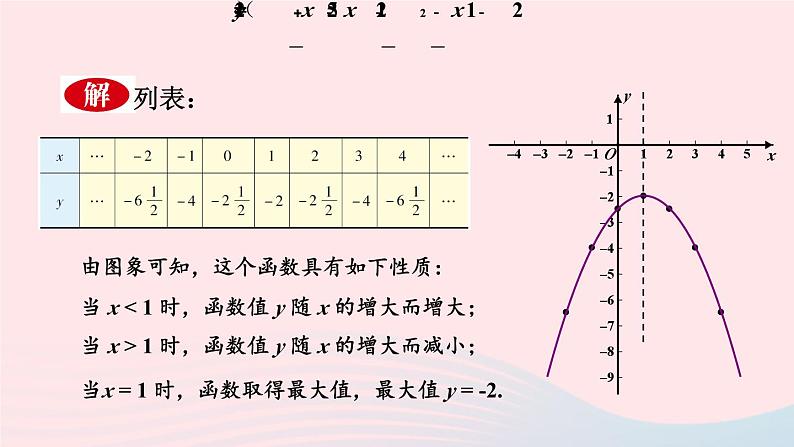
由图象可知，这个函数具有如下性质：
当 x < 1 时，函数值 y 随 x 的增大而增大；
当 x > 1 时，函数值 y 随 x 的增大而减小；
当x = 1 时，函数取得最大值，最大值 y = -2.
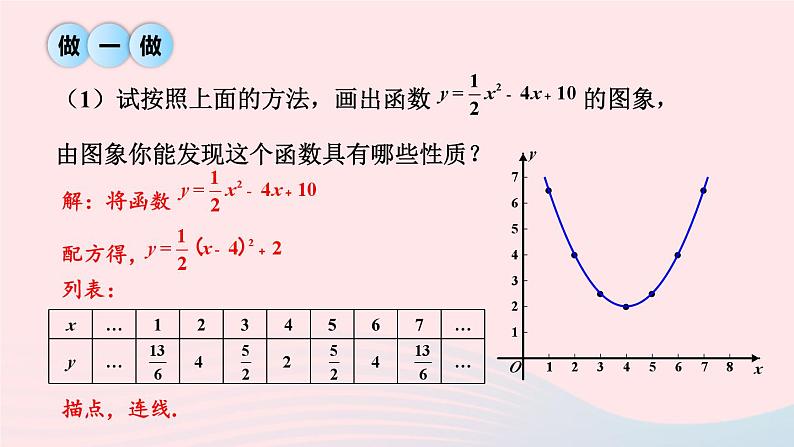
（1）试按照上面的方法，画出函数 的图象，由图象你能发现这个函数具有哪些性质？
解：将函数 配方得，
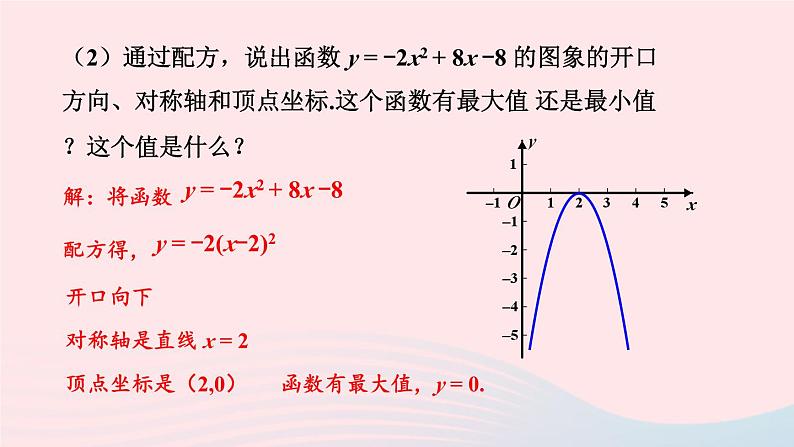
（2）通过配方，说出函数 y = -2x2 + 8x -8 的图象的开口方向、对称轴和顶点坐标.这个函数有最大值 还是最小值？这个值是什么？
y = -2x2 + 8x -8
y = -2(x-2)2
对称轴是直线 x = 2
函数有最大值，y = 0.
对于任意一个二次函数 y = ax2 + bx + c（a ≠ 0），如何确定它的图象的开口方向、对称轴和顶点坐标？你能把结果写出来吗？
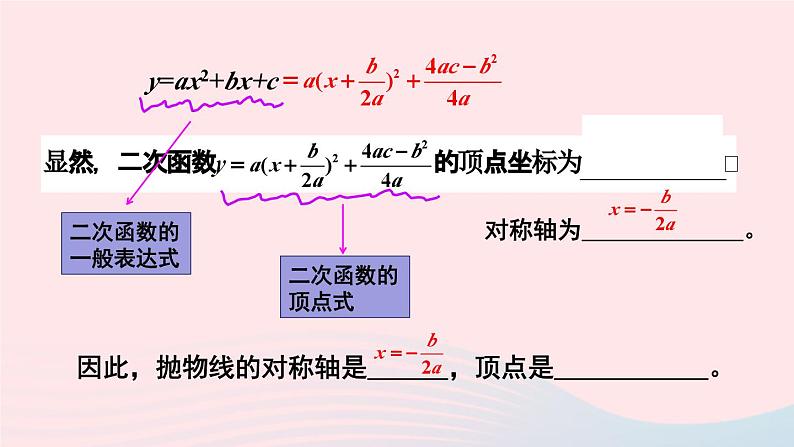
y = ax2 + bx + c（a ≠ 0）
二次函数 y = ax2 + bx + c (a ≠ 0) 通过配方可以转化成y = a(x -h)2 + k 形式.
对称轴为 。
因此，抛物线的对称轴是 ，顶点是 。
二次函数y=ax2+bx+c的图象：
1.说出下列抛物线的开口方向、对称轴和顶点坐标：
【选自教材P18 练习 第1题】
开口向上，对称轴是直线 x = -3，顶点坐标是（-3,4）.
开口向下，对称轴是直线 x = 1，顶点坐标是（1,-2）.
开口向上，对称轴是直线 x = -3，顶点坐标是（-3,-2）.
开口向下，对称轴是直线 x = 1，顶点坐标是（1,0.6）.
【选自教材P18 练习 第2题】
2. 通过配方，写出下列抛物线的开口方向、对称轴和顶点坐标：
（1）y = 2x2 + 4x ；
（2）y = -2x2 - 3x ；
（3）y = -3x2 + 6x -7；
配方得，y = 2(x + 1)2 -2开口向上，对称轴是直线 x = -1，顶点坐标是（-1,-2）.
配方得，开口向上，对称轴是直线 ，顶点坐标是 .
配方得，y = -3(x -1)2 -4开口向下，对称轴是直线 x = 1，顶点坐标是（1,-4）.
配方得，开口向下，对称轴是直线 x = 4 ，顶点坐标是 （4，13）.
【选自教材P18 练习 第3题】
3.先确定下列抛物线的开口方向、对称轴和顶点坐标，再描点画出图象：
解：开口向下，对称轴是直线 x = 1，顶点坐标是（1,4）.
解：开口向上，对称轴是直线 x = -2，顶点坐标是（-2,-5）.
解：开口向下，对称轴是直线 x = -3，顶点坐标是（-3,4）.
解：开口向上，对称轴是直线 x = 2，顶点坐标是（2,3）.