高中数学1.3 空间向量及其运算的坐标表示复习练习题

人教A版（2019）选择性必修第一册 1.3 空间向量及其运算的坐标表示

一、单选题

1．已知向量，，，则向量的坐标为（       ）.

A． B． C． D．

2．已知向量，，则（       ）

A．50 B．14 C． D．

3．已知，若，则的值为（       ）

A． B．2 C．6 D．8

4．已知空间向量，，则向量与（）的夹角为（       ）

A． B．或 C． D．或

5．若平面，的法向量分别为，，则

A． B．与相交但不垂直

C． D．或与重合

6．已知空间三点坐标分别为，，，点在平面ABC内，则实数x的值为（       ）

A．1 B． C．0 D．

7．已知空间三点，，，若向量与的夹角为60°，则实数（       ）

A．1 B．2 C． D．

8．已知，点Q在直线OP上，那么当取得最小值时，点Q的坐标是（       ）

A． B． C． D．

9．已知，，则（       ）

A． B．

C． D．

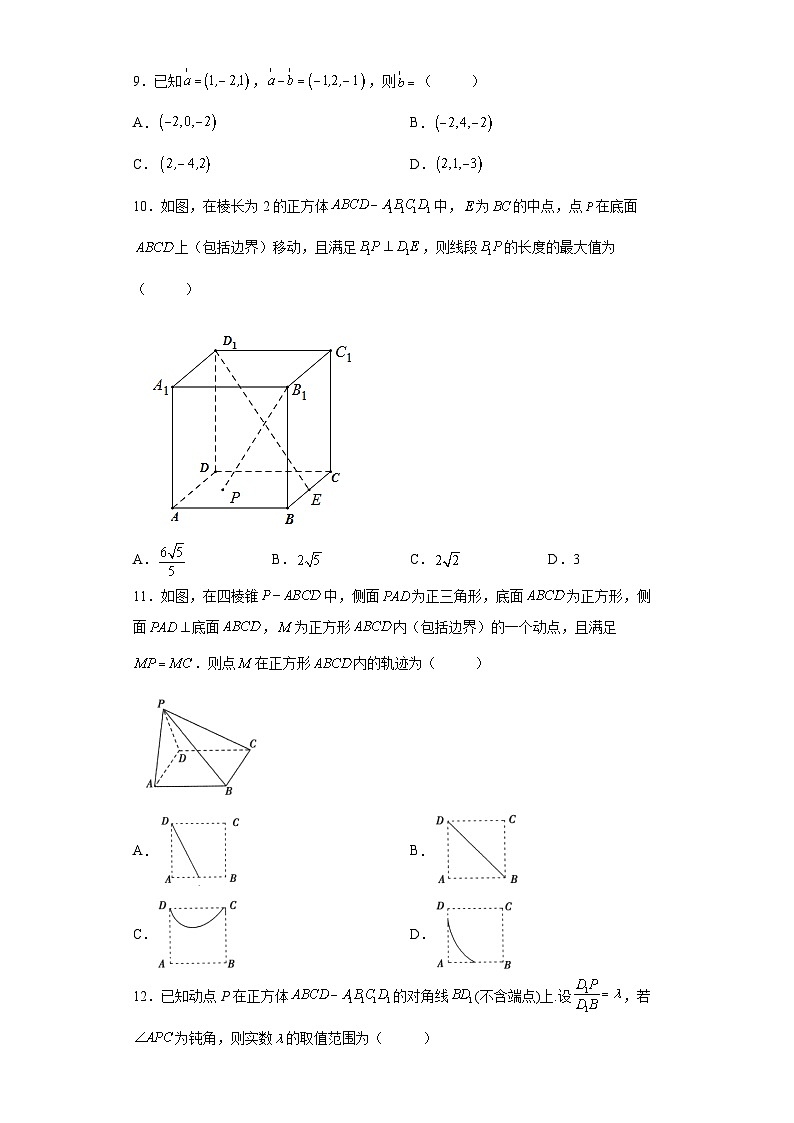
10．如图，在棱长为2的正方体中，为的中点，点在底面上（包括边界）移动，且满足，则线段的长度的最大值为（       ）

A． B． C． D．3

11．如图，在四棱锥中，侧面为正三角形，底面为正方形，侧面底面，为正方形内（包括边界）的一个动点，且满足．则点在正方形内的轨迹为（       ）

A． B．

C． D．

12．已知动点P在正方体的对角线(不含端点)上.设，若为钝角，则实数的取值范围为（       ）

A． B． C． D．

二、填空题

13．设直线的方向向量为，直线的方向向量为，若，则实数m的值为______．

14．在空间直角坐标系中，若三点A（1，-1，a），B(2，a，0)，C(1，a，-2)满足：，则实数a的值为_________.

15．已知，若与垂直，则___________.

16．已知三棱锥中，，且，长度为1的线段的端点在上，端点在侧面内运动，若的中点为，的重心为，则的最小值是_________.

三、解答题

17．如图，在长方体中，M是AC与BD的交点．若，，，求的长．

18．如图，在直三棱柱（侧棱垂直于底面的棱柱）中，，，棱，为的中点.

（1）求的长；

（2）求与所成角的余弦值.

19．如图，已知直三棱柱ABC－A1B1C1，在底面△ABC中，CA＝CB＝1，∠BCA＝90°，棱AA1＝2，M，N分别是A1B1，A1A的中点．

（1）求 的模；

（2）求cos〈，〉的值；

（3）求证：A1B⊥C1M.

20．已知向量，.

（1）计算和；

（2）求.

21．如图，以棱长为1的正方体的三条棱所在直线为坐标轴，建立空间直角坐标系，点在线段上，点在线段上.

（1）当，且点关于轴的对称点为点时，求的长度；

（2）当点是面对角线的中点，点在面对角线上运动时，探究的最小值.

参考答案：

1．A

根据空间向量线性运算的坐标表示计算，

【详解】

向量，，，

则向量，

故选：A.

【点睛】

本题考查空间向量线性运算的坐标表示，属于基础题．

2．C

根据空间向量运算的坐标表示公式、空间向量模的坐标表示公式进行求解即可.

【详解】

因为向量，，

所以.

故选：C

【点睛】

本题考查了空间向量数乘运算、加法运算、模的坐标表示公式，考查了数学运算能力.

3．C

根据向量垂直的性质计算得到答案.

【详解】

，，

则，解得.

故选：C.

4．B

根据数量积运算，结合的正负，求解对应的两个夹角.

【详解】

解得，

代入得，又向量夹角范围：

故的夹角为，则与的夹角，

当时为；时为.

故选：B.

【点睛】

本题考查空间向量的数量积，以及向量夹角的求解，属基础题.

5．A

可判断两个平面的法向量共线，根据法向量平行可知两平面平行．

【详解】

解：因为平面，的法向量分别为，

即，所以

所以

故选：A

【点睛】

本题考查了空间向量在立体几何中的应用问题，属于基础题．

6．A

先由点的坐标确定三个向量，，，再根据三点在平面ABC内，则有成立求解.

【详解】

因为，，，

所以，，

因为空间三点坐标分别为，，，点在平面ABC内

所以设，

则有.

解得

故选：A

【点睛】

本题主要考查了四点共面问题，还考查了运算求解的能力，属于基础题.

7．B

直接由空间向量的夹角公式计算即可

【详解】

，，，

，

由题意有

即，

整理得，

解得

故选：B

8．C

设，根据点在直线上，求得，再结合向量的数量积和二次函数的性质，求得时，取得最小值，即可求解.

【详解】

设，

由点在直线上，可得存在实数使得，

即，可得,

所以,

则，

根据二次函数的性质，可得当时，取得最小值，此时.

故选：C.

【点睛】

本题主要考查了空间向量的共线定理，空间向量的数量积的运算，其中解答中根据向量的数量积的运算公式，得出关于的二次函数是解答的关键，着重考查运算与求解能力.

9．C

利用空间向量的坐标运算即可求解.

【详解】

因为，，

所以，

故选：C.

10．D

以D为原点，DA为x轴，DC为y轴，为z轴，建立空间直角坐标系，利用向量法能求出线段的长度的最大值．

【详解】

解：以D为原点，DA为x轴，DC为y轴，为z轴，建立空间直角坐标系，

设P（a，b，0），则（0，0，2），E（1，2，0），（2，2，2），

＝（a−2，b−2，−2），＝（1，2，−2），

∵P⊥E，

，

∴a＋2b−2＝0，

∴点P的轨迹是一条线段，

，

由二次函数的性质可得当时，可取到最大值9，

∴线段P的长度的最大值为3．

故选：D．

【点睛】

本题考查线段长的最大值的求法，是中档题，解题时要认真审题，注意向量法的合理运用．

11．A

如图，以为坐标原点，建立空间直角坐标系，设，正方形的边长为，求出，的坐标，利用可得与的关系，即可求解.

【详解】

如图，以为坐标原点，，所在的直线分别为，轴建立如图所示的空间直角坐标系，设正方形的边长为，，则，，，，则，．由，得，

所以点在正方形内的轨迹为一条线段，

故选：A．

12．C

建立空间直角坐标系，

【详解】

由题设，建立如图所示的空间直角坐标系，用坐标法计算，利用不是平角，可得为钝角等价于，即，即可求出实数的取值范围.

设正方体的棱长为1，

则有

∴，∴设，

∴，

，

由图知不是平角，∴为钝角等价于，

∴，

∴，

解得

∴的取值范围是

故选：C.

13．##－0.5

两直线垂直，则两直线的方向向量垂直，两向量垂直，其数量积为零﹒

【详解】

∵，∴，∴．

故答案为：﹒

14．

先根据点的坐标得到，的坐标表示，再根据向量垂直对应的数量积为零计算出的值即可.

【详解】

由题意，

所以，

解得.

故答案为：

15．##

由向量垂直可得，即可求出.

【详解】

因为，

所以，，

因为与垂直，

所以，解得.

故答案为：.

16．

在平面PBC内过点P作Pz⊥PC，再建立空间直角坐标系，利用两点间距离公式探求出点T的轨迹即可得解.

【详解】

因，则平面PBC，在平面PBC内过点P作Pz⊥PC，则Pz⊥平面PAC

以点P为原点，射线PA，PC，Pz分别为x，y，z轴非负轴建立空间直角坐标系，如图：

因，则有，设，，则的中点，

连BG并延长交AC于点D，因G(m，n，p)是的重心，则D是BC中点，且，

而,，，则，即，

因，即，则，即，

所以点T的轨迹是以P为球心，为半径的球面在三棱锥内的部分(含边界)，

而，点G在上述轨迹外，且线段GP与上述轨迹必相交，

所以

故答案为：

【点睛】

结论点睛：在空间，球面外一点M与球面上点的距离最小值为点M到球心距离减去球半径；球面外一点M与球面上点的距离最大值为点M到球心距离加上球半径.

17．

以D1为原点，为x、y、z轴正方向建立空间直角坐标系，用向量法求解.

【详解】

以D1为原点，为x、y、z轴正方向建立空间直角坐标系，

则

所以，所以

即的长为.

18．（1）；（2）.

以为坐标原点，、、所在直线分别为轴、轴、轴建立空间直角坐标系.

（1）利用空间中两点间的距离公式可求得的长；

（2）利用空间向量法可求得与所成角的余弦值.

【详解】

如图，以为坐标原点，、、所在直线分别为轴、轴、轴建立空间直角坐标系.

（1）依题意得、，因此，，

因此，线段的长为；

（2）依题意得、、、，

，，

所以，，

故与所成角的余弦值为.

19．（1）；（2）；（3）证明见解析.

（1）如图，以点C作为坐标原点O，CA，CB，CC1所在直线分别为x轴，y轴，z轴，建立空间直角坐标系，利用向量的模长公式计算即可；

（2）利用坐标运算计算cos〈，〉的值；

（3）通过计算·＝0可得答案.

【详解】

（1）如图，以点C作为坐标原点O，CA，CB，CC1所在直线分别为x轴，y轴，z轴，建立空间直角坐标系. 由题意得B(0，1，0)，N(1，0，1)，

∴＝＝.

（2）由题意得A1(1，0，2)，B(0，1，0)，C(0，0，0)，B1(0，1，2)，

∴＝(1，－1，2)，＝(0，1，2)，

·＝3，||＝，||＝，

∴cos〈，〉＝＝.

（3）由题意得C1(0，0，2)，M，＝(－1，1，－2)，＝，

∴·＝－＋＋0＝0，

∴⊥，即A1B⊥C1M.

20．（1）， ；（2）.

（1）利用空间向量的坐标运算可求得的坐标，利用向量的模长公式可求得的值；

（2）计算出，结合的取值范围可求得结果.

【详解】

（1），；

（2），

，因此，.

【点睛】

本题考查空间向量的坐标运算，同时也考查了利用空间向量的数量积计算向量的夹角，考查计算能力，属于基础题.

21．（1）（2）

（1）以棱长为1的正方体的三条棱所在直线为坐标轴，建立空间直角坐标系，推导出，，由此能求出．

（2）当点是面对角线中点时，点，点在面对角线上运动，设点，，则，由此能求出当时，取得最小值为，此时点．

【详解】

（1）以棱长为1的正方体的三条棱所在直线为坐标轴，建立空间直角坐标系，

点在线段上，点在线段上．

由题意知点，

当时，，，

．

（2）当点是面对角线中点时，点，

点在面对角线上运动，设点，，

则，

当时，取得最小值为，此时点．

【点睛】

本题考查线段长的求法，考查空间直角坐标系的性质、两点间距离公式等基础知识，考查运算求解能力，是中档题．