初中数学人教版八年级上册13.3.1 等腰三角形教学课件ppt

这是一份初中数学人教版八年级上册13.3.1 等腰三角形教学课件ppt，共42页。PPT课件主要包含了学习目标，新课引入，新知学习，课堂小结，生活中的等腰三角形，钝角三角形，直角三角形，锐角三角形，第3题图，第4题图等内容，欢迎下载使用。
1. 理解并掌握等腰三角形的性质.2. 经历等腰三角形的性质的探究过程，能初步运用等腰三角形的性质解决有关问题.
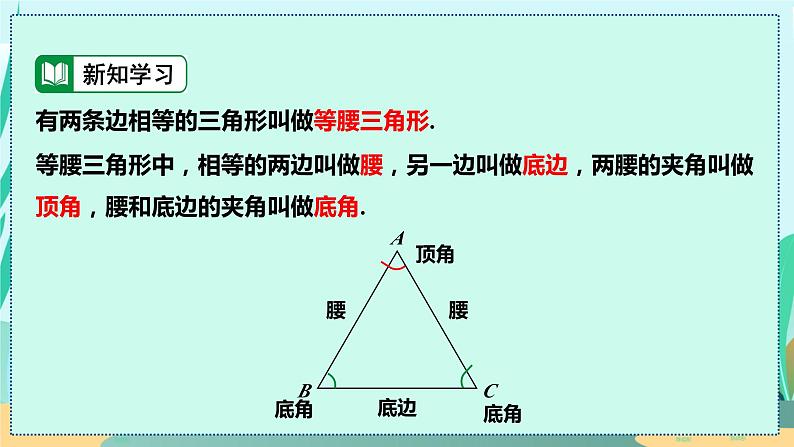
有两条边相等的三角形叫做等腰三角形.
等腰三角形中，相等的两边叫做腰，另一边叫做底边，两腰的夹角叫做顶角，腰和底边的夹角叫做底角.
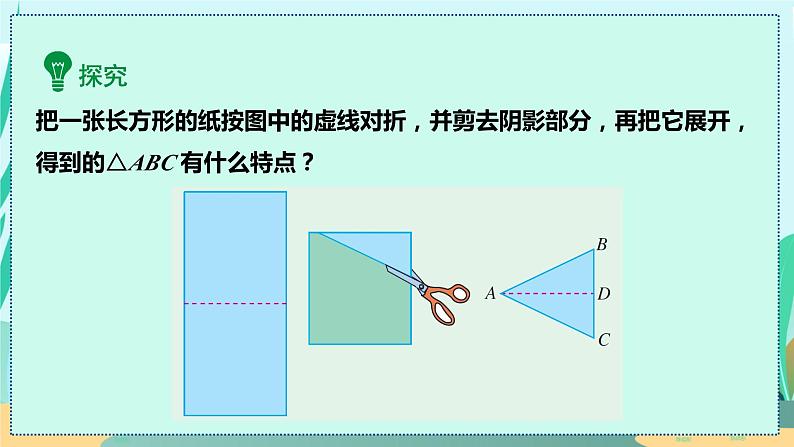
把一张长方形的纸按图中的虚线对折，并剪去阴影部分，再把它展开，得到的△ABC 有什么特点？
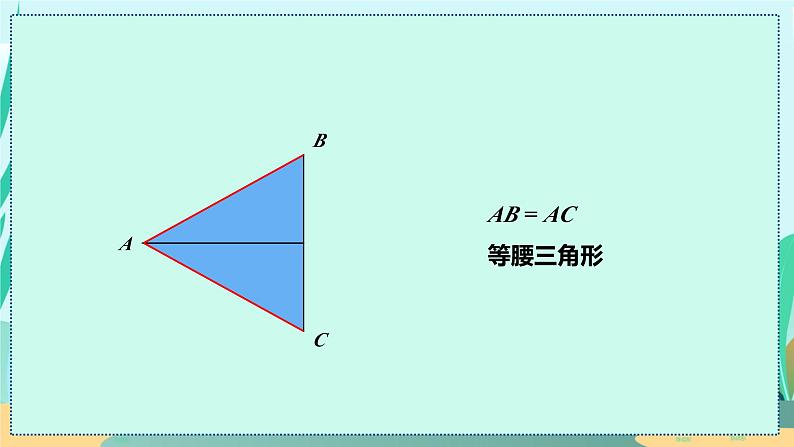
AB = AC等腰三角形
把剪出的等腰三角形沿折痕对折，△ABC 是轴对称图形吗，对称轴在哪儿？
观察重合的线段和角，猜想等腰三角形的性质.
猜想 1：等腰三角形的两个底角相等.猜想 2：等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合.
猜想：等腰三角形的两个底角相等.
已知：△ABC 中，AB = AC，求证：∠B =∠C.
证明：作底边的中线 AD，则 BD = CD.在△BAD 和△CAD 中AB = AC ( 已知 )BD = CD ( 已作 )AD = AD ( 公共边 )∴△BAD≌△CAD (SSS)∴∠B =∠C (全等三角形的对应角相等).
方法一：作底边上的中线
方法二：作顶角的平分线
证明：作顶角的平分线 AD，则∠BAD =∠CAD.在△BAD 和△CAD 中AB = AC (已知)∠BAD =∠CAD (已作)AD = AD (公共边)∴△BAD ≌△CAD (SAS)∴∠B =∠C(全等三角形的对应角相等).
方法三：作底边上的高线
证明：作 BC 边上的高线 AD.∴∠ADB=∠ADC=90°在 Rt△BAD 和 Rt△CAD 中AB = AC ( 已知 ) AD = AD ( 公共边 )∴△BAD≌△CAD (HL)∴∠B =∠C (全等三角形的对应角相等).
证明等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合.
证明：∵△BAD≌△CAD，可得 BD = CD，∠BAD =∠CAD，∠ADB=∠ADC=90°即 AD 是等腰△ABC 底边 BC 上的中线、顶角∠ BAC 的角平分线、底边BC上的高线.
性质 1：等腰三角形的两个底角相等 ( 简写成：对边对等角 ) .
应用格式：∵AB = AC∴∠B =∠C (等边对等角)
性质 2：等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合 ( 简写成：三线合一 ).
应用格式 1：∵AB = AC，AD⊥BC∴BD = CD，∠BAD =∠CAD ( 三线合一 )应用格式 2：∵AB = AC，BD = CD，∴AD⊥BC，∠BAD = ∠CAD( 三线合一 )
应用格式 3：∵AB = AC，∠BAD=∠CAD∴AD⊥BC，BD = CD ( 三线合一 )
例如图，在△ABC 中 ，AB = AC，点 D 在 AC 上，且 BD = BC = AD，求△ABC 各角的度数.
分析：(1) 指出图中有几个等腰三角形？△ABC，△ABD，△BCD.(2) 找出图中所有相等的角；∠A =∠ABD，∠C =∠BDC =∠ABC .(3) 观察∠BDC 与∠A、∠ABD 的关系.∠BDC =∠A +∠ABD = 2∠A = 2∠ABD，∠ABC -∠BDC = 2∠A，∠C =∠BDC = 2∠A.(4) 设∠A = x°∵ ∠A+∠ABC +∠C = 180°，∴x + 2x + 2x = 180.
解：∵AB = AC，BD = BC = AD，∴∠ABC =∠C =∠BDC，∠A =∠ABD.设∠A = x，则∠BDC =∠A +∠ABD = 2x，从而∠ABC =∠C =∠BDC = 2x，于是在△ABC 中，有∠A +∠ABC +∠C = x + 2x + 2x = 180°解得 x = 36°，在△ABC 中，∠A = 36°，∠ABC =∠C = 72°.
1. (1) 等腰三角形一个底角为75°，它的另外两个角为_______________；(2) 等腰三角形一个角为36°，它的另外两个角为____________________；(3) 等腰三角形一个角为120°，它的另外两个角为_______________.
72°，72° 或 36° ，108°
2.如图，△ABC 中，AB = AC，AD 和 BE 是高，它们相交于点 H，且AE = BE，求证：AH = 2BD.
分析:(1) 运用等腰三角形“三线合一”，得 2BD = BC(2) 证明△AHE≌△BCE .
证明:∵AB = AC，AD 是高，∴BC = 2BD.∵AD，BE 是高，∴∠ADC = 90°，∠AEH =∠BEC = 90°∵∠HAE +∠C = 90°，∠CBE +∠C = 90°∴∠HAE =∠CBE .在△AHE 和△BCE 中，∠HAE =∠CBE，AE = BE，∠AEH =∠BEC，∴△AHE≌△BCE(ASA). ∴AH = BC. 又∵BC = 2BD，∴AH = 2BD.
1. 说出等腰三角形的概念2. 举出等腰三角形的两个性质
两条边相等的三角形叫做等腰三角形. 等腰三角形以顶角平分线 ( 底边上的中线或底边上的高 ) 所在直线为对称轴。
性质 1：等腰三角形的两个底角相等 ( 简写成：等边对等角 ) .性质 2：等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合 ( 简写成：三线合一 ).
第1课时 等腰三角形的性质
知识点1 等腰三角形的性质：等边对等角
知识点2 等腰三角形的性质：“三线合一”
A. 等边对等角 B. 等角对等边C. 垂线段最短 D. 三线合一
角度1 利用等腰三角形的性质解决动点问题
角度2 等腰三角形边角不确定产生的分类讨论
(关键点：等腰三角形的腰不确定时,需要分类讨论)
角度3 利用等腰三角形的性质证明边角关系