陕西省咸阳市礼泉县2023届九年级下学期中考三模数学试卷(含答案)

礼泉县2023年初中学业水平考试模拟试题(三)

数学试卷

注意事项：

1.本试卷分为第一部分(选择题)和第二部分(非选择题)。全卷共6页，总分120分。考试时间120 分钟。

2.领到试卷和答题卡后，请用0.5毫米黑色墨水签字笔，分别在试卷和答题卡上填写姓名和准考证号，同时用2B铅笔在答题卡上填涂对应的试卷类型信息点(A或B)。

3.请在答题卡上各题的指定区域内作答，否则作答无效。

4.作图时，先用铅笔作图，再用规定签字笔描黑。

5.考试结束，本试卷和答题卡一并交回。

第一部分(选择题   共21分)

一、选择题(共7小题，每小题3分，计21分，每小题只有一个选项是符合题意的)

1. 的算术平方根是

                   B.                              D.5

2.如图是某几何体的平面展开图，则该几何体是

A.圆锥                   B.圆柱             C.三棱柱            D.长方体

3.如图,已知直线a∥b,直线c与a,b相交,若∠1=58°,则∠3的度数为

A.58°                   B.68°            C.122°                D.132°

4.如图，小红作了如下操作：分别以A，C为圆心，大于 长为半径作弧，两弧分别相交于点B，D，依次连接A，B，C，D，则下列说法一定正确的是

A. AB=AC                                    B. AC=BD

C. AC⊥BD                                   D.四边形ABCD是正方形

5.一次函数y=mx+5(m为常数且m<0)的图象经过A(-2,y₁)、B(3,y₂),则y₁与y₂的大小关系是

A. y₁>y₂              B. y₁=y₂              C. y₁     D. y₁≥y₂

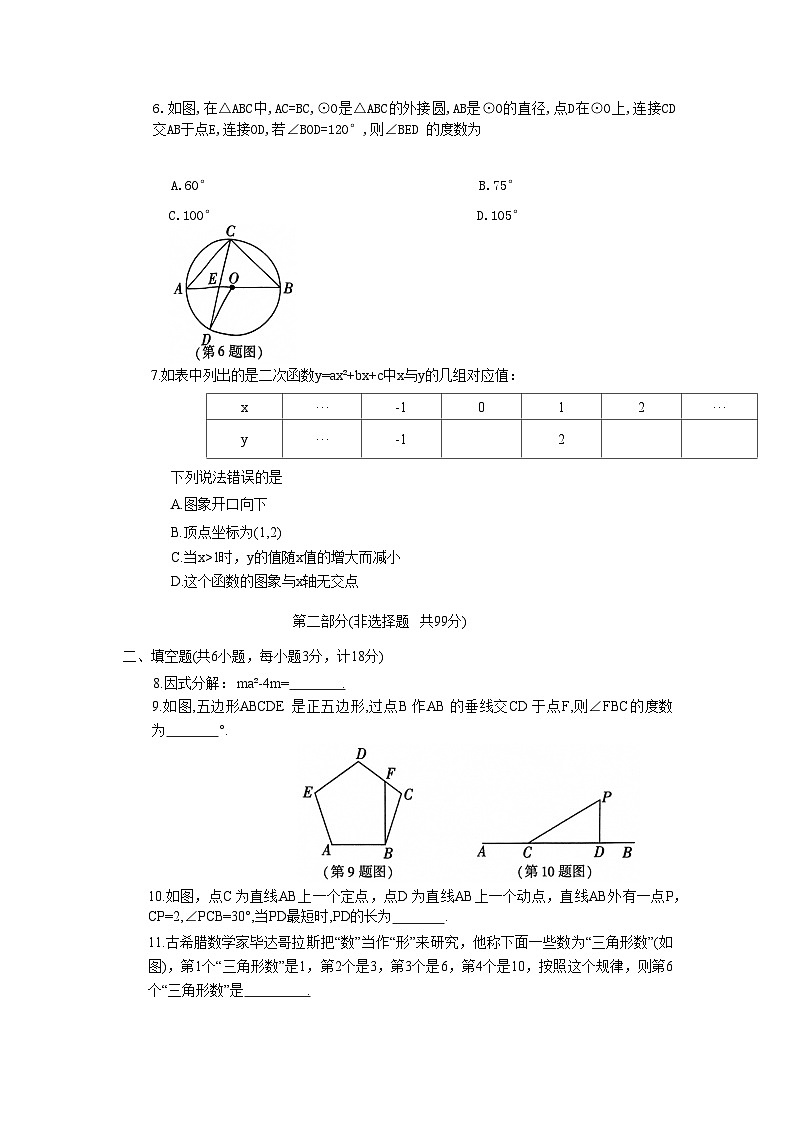
7.如表中列出的是二次函数y=ax²+bx+c中x与y的几组对应值：

下列说法错误的是

A.图象开口向下                              

B.顶点坐标为(1,2)

C.当x>1时，y的值随x值的增大而减小                 

D.这个函数的图象与x轴无交点

第二部分(非选择题   共99分)

二、填空题(共6小题，每小题3分，计18分)

8.因式分解： ma²-4m=               .

9.如图,五边形ABCDE 是正五边形,过点B 作AB 的垂线交CD 于点F,则∠FBC的度数为               °.

10.如图，点C 为直线AB上一个定点，点D 为直线AB上一个动点，直线AB外有一点P，CP=2,∠PCB=30°,当PD最短时,PD的长为               .

11.古希腊数学家毕达哥拉斯把“数”当作“形”来研究，他称下面一些数为“三角形数”(如图)，第1个“三角形数”是1，第2个是3，第3个是6，第4个是10，按照这个规律，则第6个“三角形数”是                  .

12.已知点A(a,b)在反比例函数                 的图象上，且      a²+b²=13,     则   ( a+b)²   的值为               .

13.如图,在正方形ABCD中,对角线AC、BD交于点O,点E是BC的中点,连接AE交BD于点F,GE∥AC交BD于点G,若OF=2,则AD的长为                  .

三、解答题(共14小题，计81分.解答应写出过程)

14.(本题满分4分)

计算：    

15.(本题满分4分)

求不等式组的整数解.

16.(本题满分4分)

解方程：

17.(本题满分4分)

如图，已知扇形AOB，请用尺规作图法在AB上找一点C，使得OC 将扇形AOB分成面积相等的两部分.(保留作图痕迹，不写作法)

18.(本题满分4分)

19.(本题满分5分)

女本柔弱，为母则刚，说的是母亲对子女无私的爱，母爱伟大，母亲节这天某蛋糕店制作了一款节日礼盒，按标价出售，每盒可获利50元，若该礼盒以标价的8折出售，则出售6盒与按标价降价20元出售4盒获得的利润相等，求该礼盒的成本价和标价.

20.(本题满分5分)

已知：A、B是两个整式，  A=3a²-a+1,B=2a²+a-2.

猜测：嘉淇猜测“无论a为何值，A>B始终成立”.

验证：请证明嘉淇猜测的结论.

21.(本题满分5分)

23.(本题满分7分)

某校为了进一步提高全校师生关心水、爱惜水、保护水和水忧患意识，倡导用完水及时关闭好水龙头.某班学习小组的同学合作对一个没有关紧的水龙头做漏水实验.他们用容量为500 毫升的量筒接水，每隔1分钟观察量筒中水的数据如下表：

(1)在如图所示的平面直角坐标系中描出上表中的各点，用光滑的线连接；

(2)观察图象，猜测这是什么函数的图象，并求出y与x之间的函数关系式；

(3)若按此漏水速度漏水24小时，会流失多少毫升水?

24.(本题满分7分)

“盛唐密盒”的即兴表演和互动深度融合了中国的历史文化知识，让观众在互动答题的同时，也普及了传统文化知识，也显得更加“中国”，深受广大游客的喜欢.为弘扬中华优秀传统文化，某校学生处进行了《传统文化知识》5题问答测试，随机抽取了部分学生的答题情况，并把答对题数分别制成如下的统计表和扇形统计图.

25.(本题满分8分)

26.(本题满分8分)

27.(本题满分10分)

问题提出

(1)    如图1,在▱ABCD中,AE⊥BC于点E,AF⊥CD于点F,若AB=2,BC=3,求:的值；

问题探究

问题解决

(3)如图3，某地有一足够大的空地，现想在这片空地上修建一个平行四边形状的休闲区ABCD,其中AB=600 m,点E、F、M分别在边AB、BC、AD上,管理部门欲从D到E、M到F分别修建小路，两条小路DE、MF 交汇于点O，且满足为使美观现要沿平行四边形ABCD 的四条边修建绿化带(宽度忽略不计)，求所修绿化带的长度(▱ABCD的周长).

礼泉县2023年初中学业水平考试模拟试题(三)

数学试卷参考答案及评分标准

一、选择题(共7小题，每小题3分，计21分.每小题只有一个选项是符合题意的)

1. B       2. C      3. A4. C     5. A     6. D     7. D

二、填空题(共6小题，每小题3分，计18分)

8. m( a+2) ( a-2)        9.18       10.1     1 1 .2 1  12.25

13.6【解析】由题意可得GE是△BOC的中位线， 易得△AOF∽△EGF,则得到GF=1,则OG=3,OB=6,从而得到

三、解答题(共14小题，计81分.解答应写出过程)

14.解:原式  ……………………………………………………(3分)

=4+1 -1

=4…………………………………………………………………………………………………(4分)

15.解:由  得x>1,………………………………………………………(1分)

由 得:x<4,……………………………………………………………(2分)

则不等式组的解集为1

∴不等式组的整数解为2,3………………………………………………………………………(4分)

16.解:去分母,得x(x+1)-3(x-1)=(x+1)(x-1),           ………………………………(1分)

去括号，得x²+x-3x+3=x²-1,         ……………………………………………(2分)

移项、合并同类项,得-2x=-4,           …………………………………………(3分)

解得x=2,

经检验:x=2是原方程的解…………………………………………………………………………(4分)

17.解：如图，点C即为所求.

注：①答案中线条为实线或虚线均不扣分；②没有写出结论不扣分；③其他作法正确可参考给分.

∴ DE=BF,

∴四边形DEBF 是平行四边形.……………………………………………………………………………(3分)

∴BD、EF互相平分…………………………………………………………………………………………(4分)

19.解：设该礼盒的成本价为x元，

根据题意得[0.8(x+50)-x]×6=(50-20)×4,              ……………………………(3分)

解得,x=100,……………………………………………………………………………………(4分)

100+50=150(元).

答:该礼盒的成本价为100元,标价为150元……………………………………………………………(5分)

20.证明:    A-B  =3a²-a+1 -( 2a²+a-2)

= 3a²-a+1-2a²-a+2

=a²-2a+3

=( a-1 )²+2,……………………………………………………………………(3分)

∵ (a-1)²≥0,

∴ (a-1)²+2>0,    即A-B>0,………………………………………………………(4分)

∴A>B………………………………………………………………………………(5分)

21.解: ………………………………………………………………………………………(2分)

(2)画树状图如下：

由图可知，共有12种等可能的结果，其中小灯泡发光的结果有6种，

∴小灯泡发光的概率为   …………………………………………………(5分)

注：①在(2)中如果求出的概率正确，但没有列表格或画树状图扣2分；求出概率正确，若列表或画树状图后没有就结果作出说明不扣分；②在(2)中若运用枚举法直接列举出12 种等可能结果，只要结果正确，不扣分.

解得DE=12,

∴城墙的高度DE为12米……………………………………………………………(6分)

注：没有单位，没有答语不扣分.

23.解:(1)如图所示………………………………………………………………………(1分)

(2)这是正比例函数(或一次函数)的图象,………………(2分)

设y=kx(k≠0),

将x=1,y=15代入,得k=15,

∴y与x之间的函数关系式为y=15x……………………………………………(4分)

(3)当x=24×60=1 440(分钟)时,

y=15×1 440=21 600(毫升),

∴按此漏水速度漏水24小时,会流失21 600 毫升水.……………………………(7分)

注：没有单位，没有答语不扣分.

24.解:(1)8,3,3…………………………………………………………………………(3分)

 (题).

∴所抽取学生答对题数的平均数为2.65题………………………………………(5分)

   (人).

∴估计该校学生答对5题的人数为40人…………………………………………(7分)

注：①(2)中直接写出平均数扣1分，没有答语不扣分；②(3)中没有计算过程扣1分，没有答语不扣分；③(2)、(3)不带单位均不扣分.

25.(1)证明:如图,连接OA,

(2)解:∵OD⊥AC,∴CE=EA,

∵OB=OC,∴OE为△ABC的中位线,

∴ EF=2OE=2,

∴OA=OF=3………………………………………………………………………(6分)

∵ ∠OEA=∠OAD=90°,∠AOE=∠DOA,

∴ △OEA ∽△OAD,

 即   ……………………………………………………………(7分)

∴OD=9.

∴DF=OD-OF=9-3=6.……………………………………………………………………………………(8分)

26.解:(1)在 中,令x=0,则y=4,

∴C(0,4).………………………………………………………………(1分)

令y=0,则  解得   x₁=-2,x₂=6.

∴A(-2,0),B(6,0).……………………………………………………………………………(3分)

( 2) ∵ C(0,4),∴ OC=4,

由题意知即     …………………(4分)

当x=3时,

(2)证明:在矩形ABCD中,∠B=∠BAD=90°,………………………………3分)

∴ ∠AEB=90°-∠BAE,

∵ AE ⊥DF,

∴ ∠DFA=90°-∠BAE,

∴∠AEB=∠DFA………………………………………………………………(4分)

∴△AEB∽△DFA,

 …………………………………………………………………(5分)

(3)如图,过点M作MG⊥BC于G,过点E作EH⊥CD于H,则∠MGF=∠EHD=90°,

∵∠BAD=∠EOF,

∴ ∠BAD+∠EOM=180°,

∴ ∠AEO+∠AMO=180°,

∵AD∥BC,∴ ∠GFM+∠AMO=180°,

∴∠AEO=∠GFM,………………………………………………………(7分)

∵ AB∥ CD,∴ ∠AEO=∠HDE,

∴ ∠GFM=∠HDE,

又∵∠MGF=∠EHD=90°,

∴△MGF∽△EHD,…………………………………………………………(8分)

  …………………………………………………………………………(9分)

又∵在▱ABCD 中,CD=AB=600,

∴BC=1  000,

∴▱ABCD的周长=2(AB+BC)=3 200.

故所修绿化带的长度为3 200 m…………………………………………………(10分)