人教版七年级下册5.3.2 命题、定理、证明示范课ppt课件

这是一份人教版七年级下册5.3.2 命题、定理、证明示范课ppt课件，共10页。PPT课件主要包含了对顶角相等，等量代换，等式性质等内容，欢迎下载使用。
“两点确定一条直线”“经过直线外一点有且只有一条直线与已知直线平行”“过一点有且只有一条直线和已知直线垂直”“垂线段最短”“平行于同一条直线的两直线平行” ……
“对顶角相等”“内错角相等，两直线平行” “内错角相等，两直线平行”“同旁内角互补，两直线平行”“两直线平行，内错角相等” ……
基本事实和定理可以作为继续推理的依据。
一些命题的正确性是经过推理证实的，这样得到的真命题叫做定理.
命题“在同一平面内，如果一条直线垂直于两条平行线中的一条，那么它也垂直于另一条”是真命题吗？如果是，说明理由，如果不是，请举出反例。
如图，已知直线b∥c，a⊥b。求证a⊥c。
如图1，已知直线b∥c，a⊥b.求证a⊥c.
证明： ∵a⊥b（已知）, ∴∠1=90º（垂直定义）. 又b∥c（已知）, ∴∠1=∠2（两直线平行，同位角相等）. ∴∠2=∠1=90º（等量代换）. ∴a⊥c（垂直的定义）.
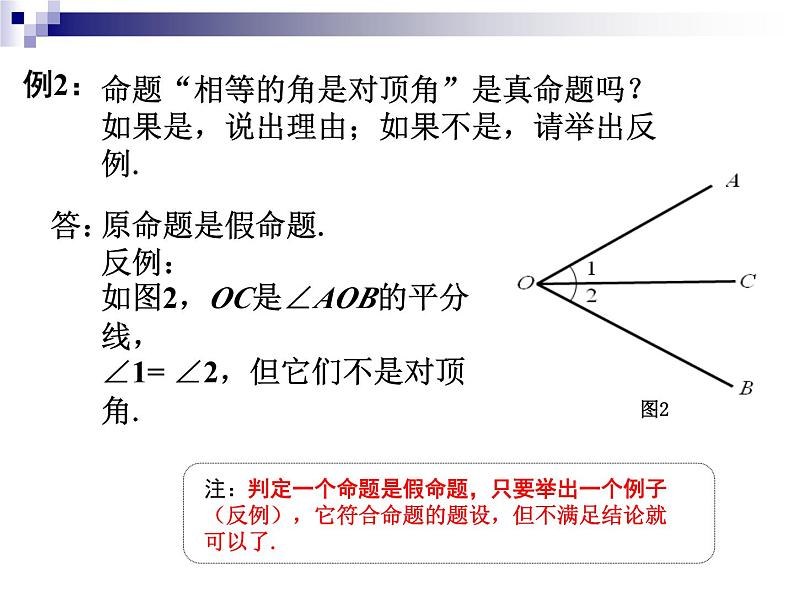
命题“相等的角是对顶角”是真命题吗？如果是，说出理由；如果不是，请举出反例.
原命题是假命题.反例：如图2，OC是∠AOB的平分线，∠1= ∠2，但它们不是对顶角.
练习1.在下面的括号内，填上推理的依据.
如图3，∠A+∠B=180º，求证∠C+∠D=180º.证明：∵∠A+∠B=180º（已知），∴AD∥BC（ ）.∴∠C+∠D=180º（ ）.
同旁内角互补，两直线平行
两直线平行，同旁内角互补
练习2.命题“同位角相等”是真命题吗？如果是，说出理由；如果不是，请举出反例.
原命题是假命题，反例：如图4，∠1与∠2是同位角， ∠1>∠2，它们不相等.
练习1　填空已知：如图1，∠1=∠2，∠3=∠4，求证：EG∥FH．证明：∵∠1=∠2（已知） ∠AEF=∠1 （ ）； ∴∠AEF=∠2 （ ）． ∴AB∥CD （ ）． ∴∠BEF=∠CFE （ ）． ∵∠3=∠4（已知）； ∴∠BEF－∠4=∠CFE－∠3． 即∠GEF=∠HFE （ ）． ∴EG∥FH （ ）．
同位角相等，两直线平行
两直线平行，内错角相等
内错角相等，两直线平行
如图，已知AB//DE，BC//EF。则∠E+∠B= 。