人教版七年级下册6.2 立方根授课ppt课件

这是一份人教版七年级下册6.2 立方根授课ppt课件，共19页。PPT课件主要包含了没有平方根，温故知新，新课引入，平方根，二次方根，立方根，三次方根，三次根号a，被开方数，根指数等内容，欢迎下载使用。
16的平方根是______
-16的平方根是________
0的平方根是________
一个正数有两个平方根,它们互为相反数;零的平方根是零,负数没有平方根.
如果一个数X的平方等于a，即　X2　=a，那么这个数X叫做a的平方根（二次方根）
要做一个体积为27cm3的正方体模型（图），它的棱长要取多少？你是怎么想到的？
如果问题中正方体的体积为10cm3，正方体的棱长又该是多少？
分析：设正方体的棱长为x㎝,则
这就是要求一个数,使它的立方等于27.
所以 x=3. 正方体的棱长为3㎝
一般的，如果一个数的 等于a，那么这个数叫做a的 或者 。
你能否根据平方根的概念，推想一下：什么是立方根呢？
算术平方根的符号 ，实际上省略了 中的根指数2。因此， 也可读作“二次根号a”
认真阅读课本第49页至第50页的内容， 完成下面练习.
1、如果一个数的立方等于a，那么这个数叫做 a 的________或_______方根，即如果x3=a，那么______ 叫做_______的立方根.
2、类似于平方根，一个数a的立方根，用符号“_______”表示，读作“___________”，其中a是 ________，3是________(根指数3不能省略，若省略表示平方根).
平方根与立方根的异同点：
如果一个数的平方等于a，那么这个数就叫a的平方根。
如果一个数的立方等于a，那么这个数就叫a的立方根。
，其中a 是被开方数，2是根指数（省略）
，其中a 是被开方数，3是根指数（不能省略）
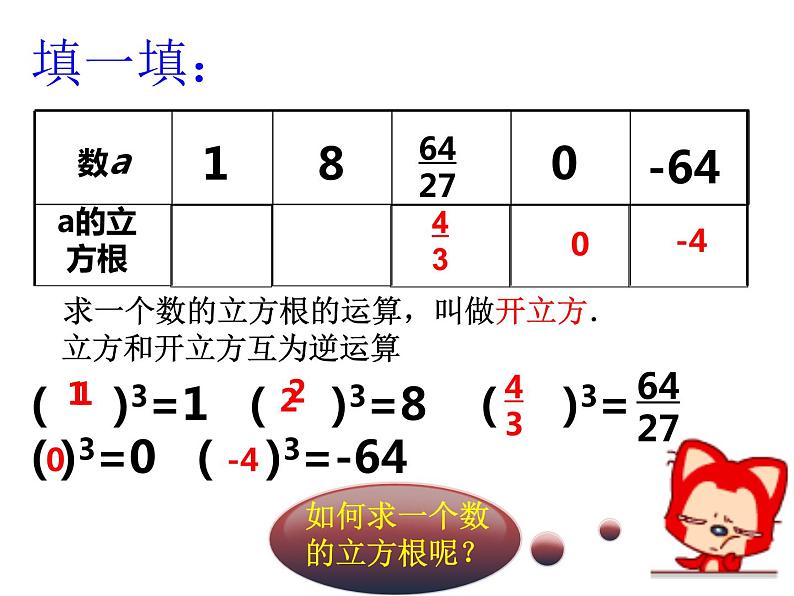
( )3=1 ( )3=8 ( )3=( )3=0 ( )3=-64
如何求一个数的立方根呢？
求一个数的立方根的运算，叫做开立方．
立方和开立方互为逆运算
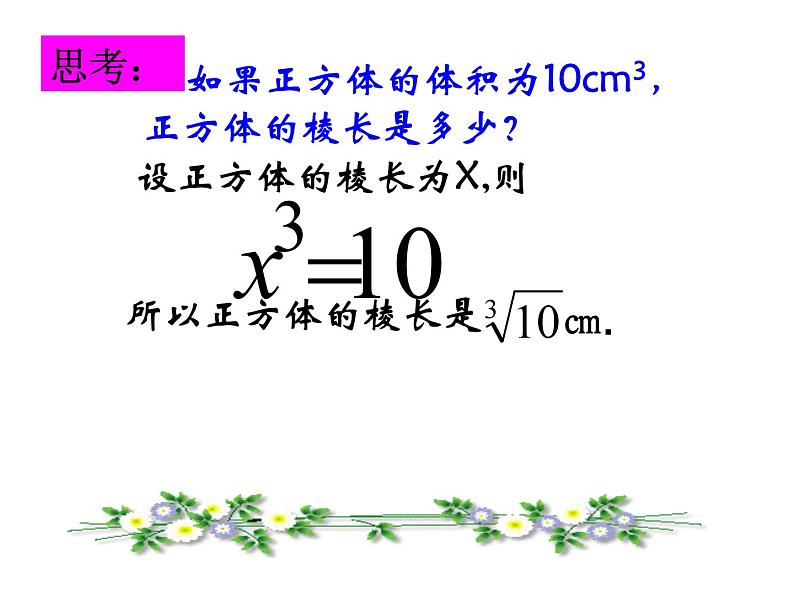
如果正方体的体积为10cm3，正方体的棱长是多少？
设正方体的棱长为X,则
4.计算 的正确结果是（ ）
A.7 B.-7 C. ±7 D.无意义
探究1： (P49)根据立方根的意义填空，看看正数、0、负数的立方根各有什么特点？
（１） 因为23 =8，所以8的立方根是（ 　 ）（２） 因为( )3 =0.125,所以0.125的立方根是（ ）（３）因为( )3 ＝０，所以０的立方根是（ 　 ）（４）因为 ( )3 ＝－8，所以－8的立方根是（ ）（５）因为( )3 ＝－ －，所以－－ 的立方根是（ ）
－ 的立方根
你能看出正数,0,负数的立方根各有什么特点?
一个数的立方根只有一个； 正数的立方根是正数； 零的立方根是零； 负数的立方根是负数。
讨论:你能归纳出平方根和立方根的异同点吗?
1.判断下列说法是否正确,并说明理由
(2) 25的平方根是5
(3) -64没有立方根
(5) 0的平方根和立方根都是0
立方根是它本身的数有哪些?
平方根是它本身的数呢?
算术平方根是它本身的数呢?
你能从上述问题中总结出互为相反数的两个数a与-a的立方根的关系吗?
互为相反数的两个数的立方根也互为相反数
求一个负数的立方根,可以先求出这个负数绝对值的立方根,然后再取它的相反数.
1.P51 练习1 、4
1.如果一个数的平方根与立方根相等，那么这个数是（ ）A.0 B.1 C.-1 D.0或1或-1
2. 的立方根是______,立方根是-0.2的数是_______.3. 计算 =_____.
4.若5x+19的立方根是4，则3x-2的平方根是_____.
5.解方程：4(2-x)3=-32
解：(2-x)3=-8，