2023新教材高中数学第4章概率与统计4.3统计模型4.3.1一元线性回归模型对点练新人教B版选择性必修第二册

这是一份2023新教材高中数学第4章概率与统计4.3统计模型4.3.1一元线性回归模型对点练新人教B版选择性必修第二册，共8页。
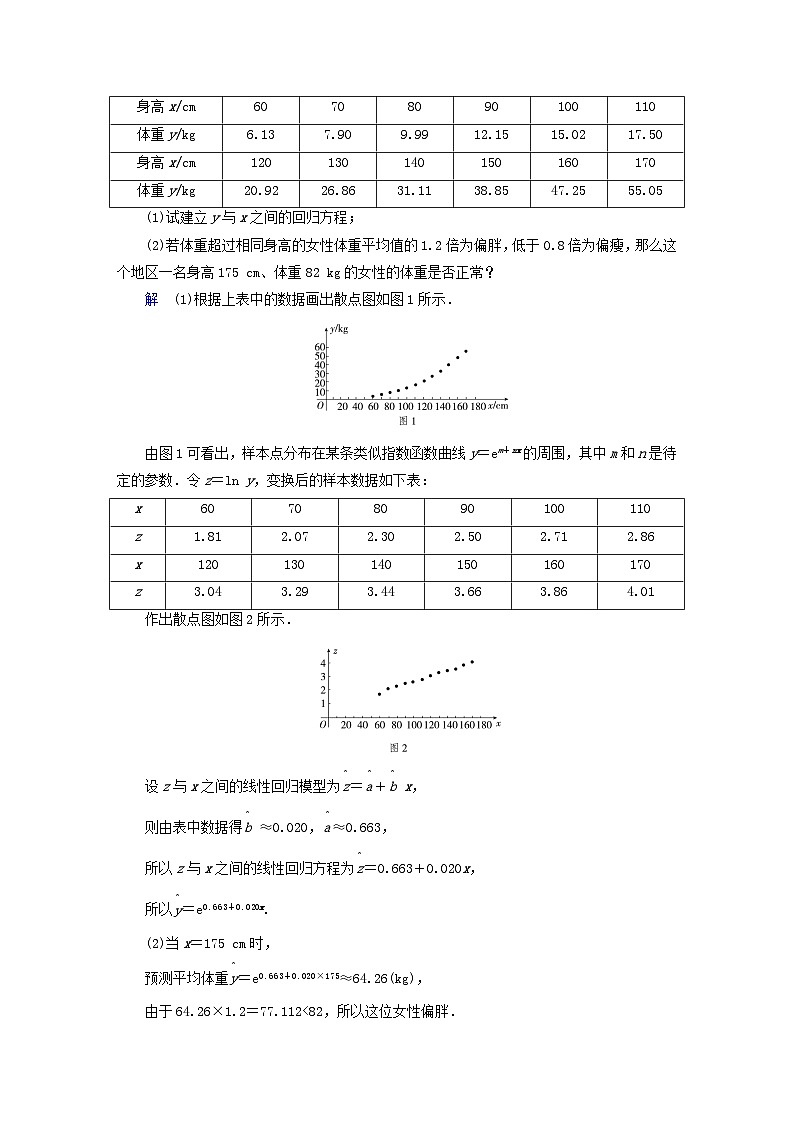
4.3　统计模型4.3.1　一元线性回归模型知识点一  相关关系1. 下列变量关系是线性相关的是(　　)A．角的大小与所对的圆弧长B．收入水平与纳税水平C．人的身高与视力D．圆的半径与面积答案　B解析　对于A，同一圆中，角的大小与弧长是确定关系，是函数关系，不是线性相关关系；对于B，是线性相关关系；对于C，人的身高与视力没有什么关系，不是线性相关关系；对于D，圆的半径与面积之间是S＝πr2，它们之间是确定的函数关系，不是线性相关关系.知识点二  回归直线方程2. 某化工厂为预测某产品的回收率y，需要研究它和原料有效成分含量x之间的相关关系，现取8对观测值，计算得i＝52，i＝228，＝478，iyi＝1849，则y与x之间的回归方程为________．答案　 ＝11.47＋2.62x解析　＝＝6.5，＝＝28.5， ＝＝≈2.62， ＝－ ≈28.5－2.62×6.5＝11.47，所以y与x之间的回归方程为＝11.47＋2.62x.3．某地最近十年粮食需求量逐年上升，下表是部分统计数据：年份20092011201320152017需求量/万吨236246257276286(1)利用所给数据求年需求量y与年份x之间的回归直线方程 ＝ x＋ ；(2)利用(1)中所求出的直线方程预测该地2020年的粮食需求量(结果保留整数)．解　(1)由所给数据可以看出，年需求量y与年份x之间是近似的线性关系，由于所给数据较大，故令u＝y－257，v＝x－2013，由上表变换后为v－4－2024u－21－1101929对处理后的数据，容易得u与v之间是近似的线性关系，计算得＝0，＝3.2.由公式计算得 ′＝6.5， ′＝－ ′＝3.2.故所求回归直线方程为 －257＝ ′(x－2013)＋ ′＝6.5(x－2013)＋3.2，即 ＝6.5(x－2013)＋260.2＝6.5x－12824.3.(2)由(1)中回归直线方程，可预测该地2020年的粮食需求量为6.5×2020－12824.3＝305.7(万吨)≈306(万吨).知识点三  回归直线方程的性质4. 为了研究变量x和y的线性相关性，甲、乙两人分别利用线性回归方法得到回归直线l1和l2，已知两人计算过程中，分别相同，则下列说法正确的是(　　)A．l1与l2一定平行B．l1与l2重合C．l1与l2相交于点(，)D．无法判断l1和l2是否相交答案　C解析　回归直线一定过样本点的中心(，)，故C正确.知识点四  相关系数5. 变量X与Y相对应的一组数据为(10,1)，(11.3,2)，(11.8,3)，(12.5,4)，(13,5)；变量U与V相对应的一组数据为(10,5)，(11.3,4)，(11.8,3)，(12.5,2)，(13,1)．r1表示变量Y与X之间的线性相关系数，r2表示变量V与U之间的线性相关系数，则(　　)A．r2<r1<0  B．0<r2<r1C．r2<0<r1  D．r2＝r1答案　C解析　对于变量X与Y而言，Y随着X的增大而增大，故变量Y与X正相关，即r1>0；对于变量U与V而言，V随着U的增大而减小，故变量V与U负相关，即r2＜0.故r2<0<r1.知识点五  非线性回归6. 某地区的女性在不同年龄段的身高平均值x(单位：cm)和体重平均值y(单位：kg)的数据如下表：身高x/cm60708090100110体重y/kg6.137.909.9912.1515.0217.50身高x/cm120130140150160170体重y/kg20.9226.8631.1138.8547.2555.05(1)试建立y与x之间的回归方程；(2)若体重超过相同身高的女性体重平均值的1.2倍为偏胖，低于0.8倍为偏瘦，那么这个地区一名身高175 cm、体重82 kg的女性的体重是否正常？解　(1)根据上表中的数据画出散点图如图1所示．由图1可看出，样本点分布在某条类似指数函数曲线y＝em＋nx的周围，其中m和n是待定的参数．令z＝ln y，变换后的样本数据如下表：x60708090100110z1.812.072.302.502.712.86x120130140150160170z3.043.293.443.663.864.01作出散点图如图2所示．设z与x之间的线性回归模型为＝＋ x，则由表中数据得 ≈0.020，≈0.663，所以z与x之间的线性回归方程为＝0.663＋0.020x，所以＝e0.663＋0.020x.(2)当x＝175 cm时，预测平均体重＝e0.663＋0.020×175≈64.26(kg)，由于64.26×1.2＝77.112<82，所以这位女性偏胖．  一、选择题1．对有线性相关关系的两个变量建立的回归直线方程 ＝ ＋ x中，回归系数 (　　)A．可以小于0  B．只能大于0C．能等于0  D．只能小于0答案　A解析　当 ＝0时，两个变量不具有线性相关性，但 可以大于0也可小于0.2．在一次试验中，测得(x，y)的四组值分别是(1,2)，(2,3)，(3,4)，(4,5)，则y与x间的回归方程为(　　)A. ＝x＋1  B． ＝x＋2C. ＝2x＋1  D． ＝x－1答案　A解析　易知变量y与x具有线性相关关系，且 ＝1，＝2.5，＝3.5，所以 ＝3.5－1×2.5＝1，故可得出线性回归方程为 ＝x＋1.故选A.3．某饮料店的日销售收入y(单位：百元)与当天平均气温x(单位：度)之间有下列数据：x－2－1012y54221甲、乙、丙三位同学对上述数据进行了研究，分别得到了x与y之间的三个线性回归方程：① ＝－x＋2.8，② ＝－x＋3，③ ＝－1.2x＋2.6.其中正确的是(　　)A．①  B．② C．③  D．①③答案　A解析　回归方程 ＝ x＋ 表示的直线必过点(，)，即必过点(0,2.8)，而给出的三个线性回归方程中，只有①表示的直线过点(0,2.8)，故正确的是①，故选A.4．用模型y＝cekx拟合一组数据时，为了求出回归方程，设z＝ln y，其变换后得到线性回归方程z＝0.3x＋4，则c＝(　　)A．0.3  B．4 C．e0.3  D．e4答案　D解析　由z＝ln y，得y＝ez.由z＝0.3x＋4，得y＝ez＝e0.3x＋4＝e4·e0.3x，所以c＝e4.故选D.5．(多选)某厂节能降耗改造后在生产A产品过程中记录的产量x(单位：吨)与相应的生产能耗y(单位：吨)的几组对应数据如下表所示，根据表中提供的数据，求出y关于x的线性回归方程为y＝0.7x＋0.35，则下列结论中正确的是(　　)x3456y2.5t44.5A．回归直线一定过点(4.5,3.5)B．产品的生产能耗与产量正相关C．t的取值必定是3.15D．A产品每多生产1吨，则相应的生产能耗增加约0.7吨答案　ABD解析　＝×(3＋4＋5＋6)＝4.5，则＝0.7×4.5＋0.35＝3.5，所以回归直线一定过点(4.5,3.5)，故A正确；因为0.7>0，所以产品的生产能耗与产量正相关，故B正确；因为＝×(2.5＋t＋4＋4.5)＝3.5，所以t＝3，故C错误；A产品每多生产1吨，则相应的生产能耗约增加0.7吨，故D正确．二、填空题6．在一组样本数据(x1，y1)，(x2，y2)，…，(xn，yn)(n≥2，x1，x2，…，xn不全相等)的散点图中，若所有样本点(xi，yi) (i＝1,2，…，n)都在直线y＝x＋1上，则这组样本数据的样本相关系数为________．答案　1解析　因为所有的样本点都落在一条直线上，所以相关系数|r|＝1，又由回归方程为y＝x＋1，说明x与y正相关，即r＞0，所以r＝1.7．某种商品的广告费支出x与销售额y之间有如下关系：(单位：万元)x24568y3040605070y与x的线性回归方程为 ＝6.5x＋17.5，当广告费支出每增加1万元，则销售额约增加________万元，当广告费支出9万元时，销售额为________万元．答案　6.5　76解析　由回归系数＝6.5可知，x每增加1个单元时， 增加6.5个单元，因此，广告费支出每增加1万元，则销售额约增加6.5万元．当广告费x＝9时， ＝6.5×9＋17.5＝76.三、解答题8．从某居民区随机抽取10个家庭，获得第i个家庭的月收入xi(单位：千元)与月储蓄yi(单位：千元)的数据资料，算得i＝80，i＝20，iyi＝184，＝720.(1)求家庭的月储蓄y对月收入x的线性回归方程 ＝ x＋ ；(2)判断变量x与y之间是正相关还是负相关；(3)若该居民区某家庭月收入为7千元，预测该家庭的月储蓄．附：线性回归方程 ＝ x＋ 中， ＝， ＝－ ，其中，为样本平均值．解　(1)由题意知n＝10，＝i＝＝8，＝i＝＝2，又－n2＝720－10×82＝80，iyi－n＝184－10×8×2＝24，由此得 ＝＝＝0.3， ＝－ ＝2－0.3×8＝－0.4，故所求回归方程为 ＝0.3x－0.4.(2)由于变量y的值随x的值增加而增加( ＝0.3>0)，故x与y之间是正相关．(3)将x＝7代入回归方程，可以预测该家庭的月储蓄为y＝0.3×7－0.4＝1.7千元．9．为了对某市中考成绩进行分析，所有成绩均已按百分制进行了折算，在60分以上的全体同学中随机抽出8位，若这8位同学的数学、物理、化学分数对应如下表：学生编号12345678数学分数x6065707580859095物理分数y7277808488909395化学分数z6772768084879092(1)用变量y与x，z与x的相关系数说明物理与数学、化学与数学的相关程度；(2)求y与x，z与x的线性回归方程(系数精确到0.01)．(参考数据：＝77.5，＝85，＝81， (xi－)2≈1050， (yi－)2≈456， (zi－)2≈550， (xi－)(yi－)≈668， (xi－)(zi－)≈755， (yi－i)2≈7， (zi－i)2≈94，≈32.4，≈21.4，≈23.5)解　(1)变量y与x，z与x的相关系数分别是r＝≈0.99，r′＝≈0.99.可以看出，物理与数学、化学与数学的成绩都是高度正相关的．(2)设y与x，z与x的线性回归方程分别是＝x＋，＝′x＋′.根据所给的数据，可以计算出＝≈0.66，≈85－0.66×77.5＝33.85，′＝≈0.72，′≈81－0.72×77.5＝25.20.所以y与x和z与x的回归方程分别是＝0.66x＋33.85，＝0.72x＋25.20.10．在彩色显像中，根据以往的经验，知道染料光学密度y与析出银的光学密度x之间的关系可用函数y＝A(b<0)进行拟合．我们通过11次试验得到如下数据：x0.050.060.070.100.140.20y0.100.140.230.370.590.79x0.250.310.380.430.47 y1.001.121.191.251.29 试确定参数A，b的值．解　对y＝A (b<0)两边取自然对数，得ln y＝ln A＋.取u＝，v＝ln y，a＝ln A，则v＝a＋bu，这是v对u的线性回归方程．题设中所给的数据经变量置换u＝，v＝ln y，变为如表所示的数据：u20.00016.66714.28610.0007.1435.000v－2.303－1.966－1.470－0.994－0.528－0.236u4.0003.2262.6322.3262.128 v00.1130.1740.2230.255 得≈7.946，＝－0.612，得 ≈－0.146， ≈0.548，所以 ＝0.548－0.146u.把u和v换回来可得ln  ＝0.548－，所以 ＝，所以A＝e0.548，b＝－0.146.