中考数学复习第三章函数第9课时平面直角坐标系与函数课件

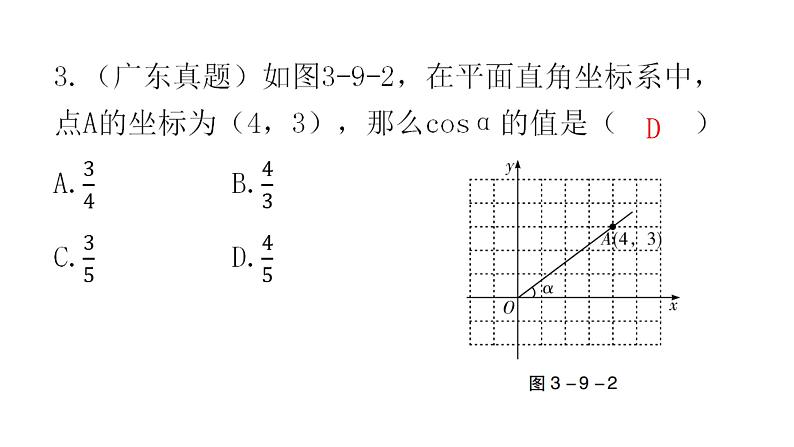
这是一份中考数学复习第三章函数第9课时平面直角坐标系与函数课件，共57页。PPT课件主要包含了课前循环练，新课标，考点梳理，广东中考，高分击破，中考演练，命题趋势，限时5分钟，＜m＜1，纵坐标等内容，欢迎下载使用。
1.（广东真题）在平面直角坐标系中，点P（-2，-3）所在的象限是（ ）A.第一象限B.第二象限C.第三象限D.第四象限
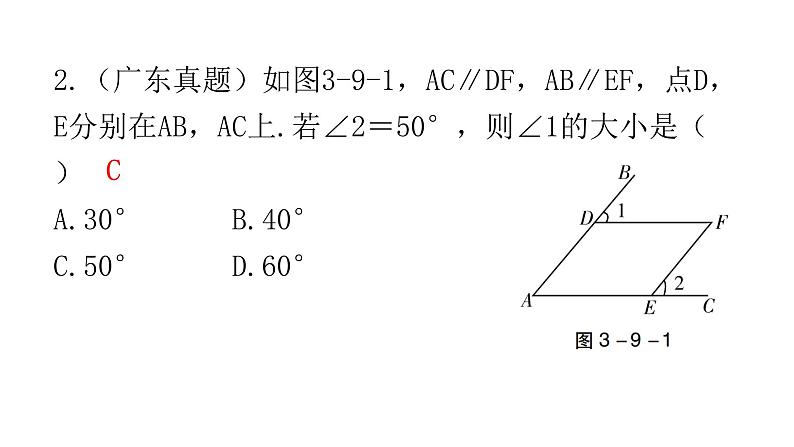
2.（广东真题）如图3-9-1，AC∥DF，AB∥EF，点D，E分别在AB，AC上.若∠2＝50°，则∠1的大小是（ ）A.30°B.40°C.50°D.60°
4.（广东真题）某市2007年、2009年商品房每平方米的平均价格分别为4 000元、5 760元.假设2007年后的两年内，商品房每平方米平均价格的年增长率都为x，那么可列出关于x的方程为___ _________________.
4 000（1+x）2＝5 760
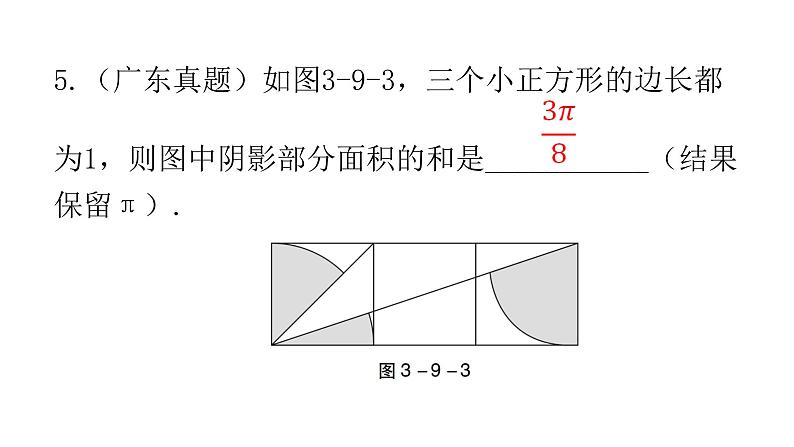
5.（广东真题）如图3-9-3，三个小正方形的边长都为1，则图中阴影部分面积的和是___________（结果保留π）.
（1）平面直角坐标系①理解平面直角坐标系的有关概念，能画出平面直角坐标系；在给定的平面直角坐标系中，能根据坐标描出点的位置，由点的位置写出坐标.②在实际问题中，能建立适当的平面直角坐标系，描述物体的位置.
③对给定的正方形，会选择合适的平面直角坐标系，写出它的顶点坐标，体会可以用坐标表达简单图形.④在平面直角坐标系中，以坐标轴为对称轴，能写出一个已知顶点坐标的多边形的对称图形的顶点坐标，知道对应顶点坐标之间的关系.
⑤在平面直角坐标系中，能写出一个已知顶点坐标的多边形沿坐标轴方向平移一定距离后图形的顶点坐标，知道对应顶点坐标之间的关系.⑥在平面直角坐标系中，探索并了解将一个多边形依次沿两个坐标轴方向平移后所得到的图形和原来图形具有平移关系，体会图形顶点坐标的变化.
（2）函数①探索简单实例中的数量关系和变化规律，了解常量、变量的意义；了解函数的概念和表示法，能举出函数的实例.②能结合图象对简单实际问题中的函数关系进行分析.③能确定简单实际问题中函数自变量的取值范围，会求函数值.
④能用适当的函数表示法刻画简单实际问题中变量之间的关系，理解函数值的意义（新增）.⑤结合对函数关系的分析，能对变量的变化情况进行初步讨论.
人教：七下第七章 平面直角坐标系； 八下第十九章 一次函数（19.1函数）北师：七下第三章 变量之间的关系； 八上第三章 位置与坐标
1.平面直角坐标系在平面内，两条互相___________且有公共_________的数轴组成平面直角坐标系.平面直角坐标系中的点和有序实数对是___________对应的
例1.如果用有序数对 (3,2)表示教室里第3列第2排的座位，则位于第5列第4排的座位应记作___________.
2.各象限内点的坐标特征（如图3-9-4）（1）若点 P(a,b)在第一象限，则a＞0，b＞0；（2）若点 P(a,b)在第二象限，则 a________0，b________0；（3）若点 P(a,b)在第三象限，则a________0，b________0；
（4）若点 P(a,b)在第四象限，则 a______0，b______0；（5）坐标轴上的点不属于任何象限
例2.在平面直角坐标系中，若点M(m-1,m)在第二象限，则 m 的取值范围是___________.
3.与坐标轴有关的点的坐标特征（1）坐标轴上点的特征：x轴上的点的___________为0；y轴上的点的___________为0；原点的坐标为___________.
（2）平行于坐标轴的直线上点的坐标特征：①若两个点在平行于 x 轴的直线上，则___________相同，___________不同；②若两个点在平行于 y 轴的直线上，则___________相同，___________不同
例3.如图3-9-5，将□ABCO放置在平面直角坐标系xOy中，O 为坐标原点.若点A的坐标是 (6,0)，点C的坐标是（1,4），则点 B 的坐标是___________.
4.对称点的坐标特征点P(a,b)关于 x 轴的对称点 P1 的坐标为_________；点P(a,b)关于 y 轴的对称点 P2 的坐标为_________；点P(a,b)关于原点的对称点 P3 的坐标为_________
例4.在平面直角坐标系中，点 P（3,-2）关于 y 轴的对称点的坐标是___________，关于原点的对称点的坐标是___________.
5.点的坐标平移变化规律（1）点（a，b）向右平移m个单位长度可得到点（a+m，b）；点（a，b）向左平移m个单位长度可得到点（a-m，b）；点（a，b）向上平移n个单位长度可得到点（a，b+n）；点（a，b）向下平移n个单位长度可得到点（a，b-n）.（2）根据其规律可得口诀：左右平移→左减右加纵不变；上下平移→上加下减横不变
例5.在平面直角坐标系中，将点（-4,-6）先向右平移4个单位长度，再向上平移 6 个单位长度得到点A，则点A的坐标为___________.
6.坐标与距离点P（a,b）到 x 轴的距离为___________，到 y 轴的距离为___________，到原点的距离为___________
例6.已知点 P 在第四象限，且到 x 轴的距离是 3，到 y 轴的距离是 2，则点 P 的坐标为___________.
7.函数的有关概念（1）变量与常量:在一个变化过程中，我们称数值发生变化的量为变量，数值始终不变的量为常量.（2）函数的概念:一般地,在一个变化过程中，如果有两个变量x与y，并且对于x的每一个确定的值，y都有唯一确定的值与其对应，那么我们就说x是自变量，y是x的函数.
（3）表示方法:________法、_______法、_______法.（4）自变量的取值范围①解析式是整式时，自变量的取值范围是__________；②解析式是分式时，自变量的取值范围是____________________；③解析式是二次根式时，自变量的取值范围是_______________________.（5）函数值：对于一个函数，如果当x=a时y=b,那么b叫做当自变量的值为a时的函数值
8.函数的图象（1）函数图象的概念:一般地,对于一个函数，如果把自变量与函数的每对对应值分别作为点的横、纵坐标，那么坐标平面内由这些点组成的图形，就是这个函数的图象.（2）描点法画函数图象的一般步骤:列表、描点、连线
例8.小明从家出发步行至学校，停留一段时间后乘车返回，则下列函数图象最能体现他离家的距离s与出发时间t之间的对应关系的是（ ）
1.（2020·广东，关于x轴、y轴对称的点的坐标）在平面直角坐标系中，点（3，2）关于x轴对称的点的坐标为（ ）A.（-3，2）B.（-2，3）C.（2，-3）D.（3，-2）
2.（2022·广东，点的坐标平移）在平面直角坐标系中，将点（1，1）向右平移2个单位长度后，得到的点的坐标是（ ）A.（3，1）B.（-1，1）C.（1，3）D.（1，-1）
3.（2022·广东，常量与变量）水中涟漪（圆形水波）不断扩大，记它的半径为r，则圆周长C与r的关系式为C＝2πr.下列判断正确的是（ ）A.2是变量B.π是变量C.r是变量D.C是常量
1.（2022·鄂州）在“看图说故事”活动中，某学习小组设计了一个问题情境：小明从家跑步去体育场，在那里锻炼了一阵后又走到文具店买圆规，然后散步走回家.小明离家的距离y（km）与他所用的时间x（min）的关系如图3-9-6所示：
（1）小明家离体育场的距离为___________km，小明跑步的平均速度为___________km/min；（2）当15≤x≤45时，请直接写出y关于x的函数表达式；（3）当小明离家2 km时，求他离开家所用的时间.
温馨提示：此类考题常见于广东省中考数学试卷的第20小题，分值一般为9分，答题时要注意书写格式，分步书写，慢做会求全对，评卷老师是分步给分的哦！
【典型错例】不会用绝对值表示距离和分类讨论
2.已知点P（2-m，2m+6），且点P到两坐标轴的距离相等，求点P的坐标.
【变式考点】平面直角坐标系与点的坐标综合运用
3.已知点A（a-2，-2），B（-2，b+1），根据以下要求确定a，b的值.（1）点A在y轴上，点B关于x轴对称的点为（-2，3）；（2）A，B两点在第一、三象限的角平分线上.
解：（1）由题意，得a-2＝0，b+1+3＝0.解得a＝2，b＝-4.（2）由题意，得a-2＝-2，b+1＝-2.解得a＝0，b＝-3.
【创新考点】平面直角坐标系的新定义题型
一、选择题1.（2022·乐山）点P（-1，2）在（ ）A.第一象限B.第二象限C.第三象限D.第四象限
2.（2022·新疆）在平面直角坐标系中，点A（2，1）与点B关于x轴对称，则点B的坐标是（ ）A.（2，-1）B.（-2，1）C.（-2，-1）D.（2，1）3.（2022·贵港）若点A（a，-1）与点B（2，b）关于y轴对称，则a-b的值是（ ）A.-1B.-3C.1D.2
4.（2022·铜仁）如图3-9-7，在矩形ABCD中，A（-3，2），B（3，2），C（3，-1），则点D的坐标为（ ）A.（-2，-1）B.（4，-1）C.（-3，-2）D.（-3，-1）
5.（2022·北京）下面的三个问题中都有两个变量：①汽车从A地匀速行驶到B地，汽车的剩余路程y与行驶时间x；②将水箱中的水匀速放出，直至放完，水箱中的剩余水量y与放水时间x；③用长度一定的绳子围成一个矩形，矩形的面积y与一边长x.其中，变量y与变量x之间的函数关系可以用如图3-9-8所示的图象表示的是（ ）A.①②B.①③C.②③D.①②③
二、填空题6.（2022·泸州）点（-2，3）关于原点的对称点的坐标为___________.7.（2022·广安）若点P（m+1，m）在第四象限，则点Q（-3，m+2）在第__________象限.
8.（2022·烟台）观察如图3-9-9所示的象棋棋盘，若“兵”所在的位置用（1，3）表示，“炮”所在的位置用（6，4）表示，那么“帅”所在的位置可表示为___________.
三、解答题9.（教材改编）已知点P（2a-3，a+1），请分别根据下列条件，求出点P的坐标.（1）点P在x轴上；（2）点P的纵坐标比横坐标大2.
解：（1）∵点P（2a-3，a+1）在x轴上，∴a+1＝0.解得a＝-1.∴2a-3＝2×（-1）-3＝-5.∴点P的坐标为（-5，0）.（2）∵点P（2a-3，a+1）的纵坐标比横坐标大2，∴a+1-（2a-3）＝2.解得a＝2.∴2a-3＝2×2-3＝1，a+1＝2+1＝3.∴点P的坐标为（1，3）.
10.（教材改编）已知点M（2a+5，a-2）在第四象限，分别根据下列条件求点M的坐标.（1）点M到x轴的距离为3；（2）点N的坐标为（5，-4），且直线MN与坐标轴平行.
解：（1）∵点M到x轴的距离为3，∴a-2＝3或a-2＝-3.解得a＝5或a=-1.∴点M的坐标为（15，3）或（3，-3）.∵点M在第四象限，∴点M的坐标为（3，-3）.
（2）当直线MN与x轴平行时，得a-2＝-4.解得a＝-2.∴2a+5＝2×(-2)+5＝1.∴点M的坐标为（1，-4）；当直线MN与y轴平行时，得2a+5＝5.解得a＝0.∴a-2＝-2.∴点M的坐标为（5，-2）.综上所述，点M的坐标为（1，-4）或（5，-2）.
（运算能力；应用意识；创新意识）在平面直角坐标系中，给出如下定义：点A到x轴、y轴距离的较大值称为点A的“长距”，当点P的“长距”等于点Q的“长距”时，称P，Q两点为“等距点”.（1）求点A（-5，2）的“长距”；（2）若C（-1，k+3），D（4，4k-3）两点为“等距点”，求k的值.