中考数学复习第四章三角形第17课时相似三角形课件

这是一份中考数学复习第四章三角形第17课时相似三角形课件，共60页。PPT课件主要包含了课前循环练，新课标，考点梳理，广东中考，高分击破，中考演练，命题趋势，限时5分钟，adbc，成比例等内容，欢迎下载使用。

1.（广东真题）坐标平面内下列各点中，在x轴上的点是（ ）A.（0，3）B.（-3，0）C.（-1，2）D.（-2，-3）
2.（广东真题）水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示，如图4-17-1是一个正方体的表面展开图，若图中“2”在正方体的前面，则这个正方体的后面是（ ）A.0B.6C.快D.乐
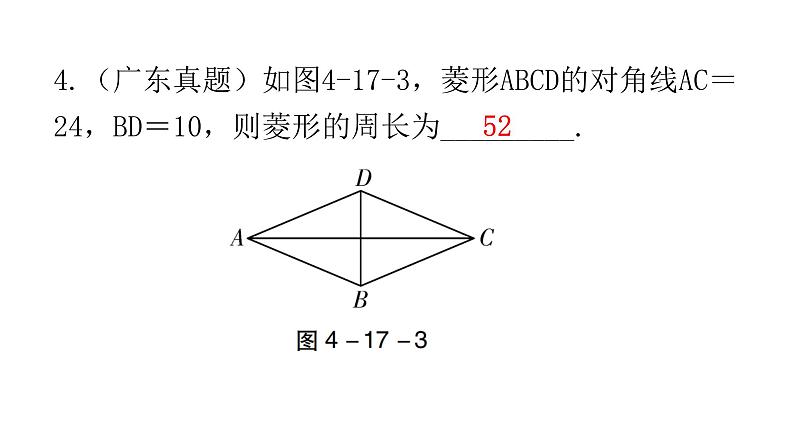
4.（广东真题）如图4-17-3，菱形ABCD的对角线AC＝24，BD＝10，则菱形的周长为_________.
①了解比例的基本性质、线段的比、成比例的线段；通过建筑、艺术上的实例了解黄金分割.②通过具体实例认识图形的相似.了解相似多边形和相似比.③掌握基本事实：两条直线被一组平行线所截，所得的对应线段成比例.
④了解相似三角形的判定定理：两角分别相等的两个三角形相似；两边成比例且夹角相等的两个三角形相似；三边成比例的两个三角形相似.*了解相似三角形判定定理的证明.⑤了解相似三角形的性质定理：相似三角形对应线段的比等于相似比；面积比等于相似比的平方.⑥了解图形的位似，知道利用位似可以将一个图形放大或缩小.
⑦会利用图形的相似解决一些简单的实际问题.⑧在平面直角坐标系中，探索并了解将一个多边形的顶点坐标（有一个顶点为原点）分别扩大或缩小相同倍数时所对应的图形与原图形是位似的．
人教：九下第二十七章 相似北师：九上第四章 图形的相似
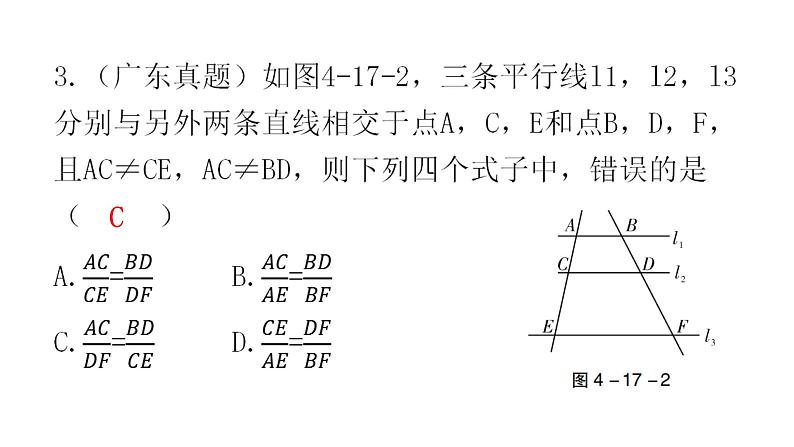
（4）平行线分线段成比例的基本事实：两条直线被一组平行线所截，所得的对应线段成比例.推论：平行于三角形一边的直线截其他两边（或两边的延长线），所得的对应线段成比例
3.相似三角形三角分别_________、三边___________的两个三角形叫做相似三角形，相似三角形对应边的比叫做相似比
例3.已知△ABC∽△ACD，若 AB=5，AC=4，则 AD=__________.
4.相似三角形的判定（1）两角分别___________的两个三角形相似.（2）两边___________且夹角___________的两个三角形相似.（3）三边___________的两个三角形相似.（4）平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似
例4.如图4-17-6，P是□ABCD 边 AB 上的一点，射线 CP 交 DA 的延长线于点 E，请从图中找出一对相似三角形：______ ____________________.
△EAP∽△EDC（答案不唯一）
5.相似三角形的性质（1）相似三角形对应高的比、对应角平分线的比、对应中线的比都等于___________.（2）相似三角形的周长比等于___________，面积比等于________________
6.相似多边形各角分别___________、各边___________的两个多边形叫做相似多边形，相似多边形对应边的比叫做___________
例6.如图4-17-7所示的两个四边形相似，则 x+y=_________，α=_________.
7.相似多边形的性质（1）相似多边形的对应角相等，对应边的比等于相似比.（2）相似多边形的周长比等于___________，面积比等于____________________
例7.已知正方形 ABCD 的面积为 9 cm2，正方形A1B1C1D1的面积为 16 cm2，则两个正方形ABCD与正方形A1B1C1D1的相似比为___________.
8.图形的位似（1）位似图形的定义：如果两个图形不仅相似，而且每组对应点所在直线都经过同一点，那么这样的两个图形叫做位似图形，这个点叫做位似中心，此时相似比又称位似比.（2）位似图形的性质①位似图形上任意一对对应点到位似中心的距离之比等于___________；
②位似图形的对应角_________，对应边__________；③位似图形的对应线段___________（或在同一条直线上）；④在平面直角坐标系中，将一个多边形每个顶点的横坐标、纵坐标都乘同一个数 k（k≠0），所对应的图形与原图形___________，位似中心是___________，它们的相似比为_________
例8.如图4-17-8，在边长为 1 的正方形网格中，有一个△ABC，已知 A，B，C 三点的坐标分别是 A（1,0），B（2,-1），C（3,1）.（1）请在网格图形中画出平面直角坐标系；（2）以原点O 为位似中心，将△ABC 放大 2 倍，画出放大后的△A′B′C′（画一个即可）；
（3）写出△A′B′C′各顶点的坐标：A′___________，B′___________，C′___________.
1.（2022·江西）如图4-17-10，四边形ABCD为菱形，点E在AC的延长线上，∠ACD＝∠ABE.（1）求证：△ABC∽△AEB；（2）当AB＝6，AC＝4时，求AE的长.
（1）证明：∵四边形ABCD为菱形，∴∠ACD＝∠ACB.···1分（利用菱形的性质得1分）∵∠ACD＝∠ABE，∴∠ACB＝∠ABE.······2分（等量代换得1分）又∵∠BAC＝∠EAB，∴△ABC∽△AEB.···4分（利用相似三角形的判定得2分）
温馨提示：此类考题常见于广东省中考数学试卷的第18小题，分值一般为8分，答题时要注意书写格式，分步书写，慢做会求全对，评卷老师是分步给分的哦！
【典型错例】相似三角形中的分类讨论
2.如图4-17-11，在△ABC中，AB＝8，AC＝6，点D在边AC上，且AD＝2，在AB上是否存在一点E，使得△ADE与△ABC相似？若存在，求出所有符合条件的AE的长；若不存在，说明理由.
【变式考点】相似三角形的判定与性质的应用
3.（2021·湖北）如图4-17-13，在△ABC和△DEC中，∠A＝∠D，∠BCE＝∠ACD.（1）求证：△ABC∽△DEC；（2）若S△ABC∶S△DEC＝4∶9，BC＝6，求EC的长.
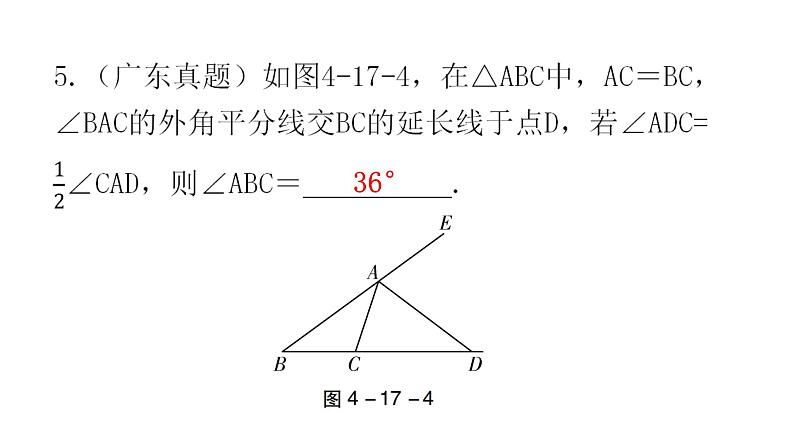
【创新考点】黄金分割；等腰三角形的性质
4.（2022·连云港）△ABC的三边长分别为2，3，4，另有一个与它相似的△DEF，其最长边为12，则△DEF的周长是（ ）A.54B.36C.27D.21
二、填空题6.（2022·邵阳）如图4-17-18，在△ABC中，点D在边AB上，点E在边AC上，请添加一个条件________________________________，使△ADE∽△ABC.
7.（2021·湘潭）如图4-17-19，在△ABC中，D，E分别为边AB，AC上的点，试添加一个条件：____________________________，使得△ADE与△ABC相似.（任意写出一个满足条件的即可）
8.（2022·成都）如图4-17-20，△ABC和△DEF是以点O为位似中心的位似图形.若OA∶AD＝2∶3，则△ABC与△DEF的周长比是___________.
三、解答题9.（2020·乐山）如图4-17-21，E是矩形ABCD的边CB上的一点，AF⊥DE于点F，AB＝3，AD＝2，CE＝1.求DF的长度.