中考数学复习第六章圆第21课时圆的有关概念及性质课件

这是一份中考数学复习第六章圆第21课时圆的有关概念及性质课件，共55页。PPT课件主要包含了课前循环练，新课标，考点梳理，广东中考，高分击破，中考演练，命题趋势，过圆心，两点间，垂直平分等内容，欢迎下载使用。

1.（广东真题）计算的结果是-1的式子是（ ）A.-|-1|B.（-1）0C.-（-1）D.1-12.（广东真题）将4个红球、3个白球、2个黑球放入一个不透明的袋子里，从中摸出8个球，恰好红球、白球、黑球都摸到，这件事情（ ）A.可能发生B.不可能发生C.很可能发生D.必然发生
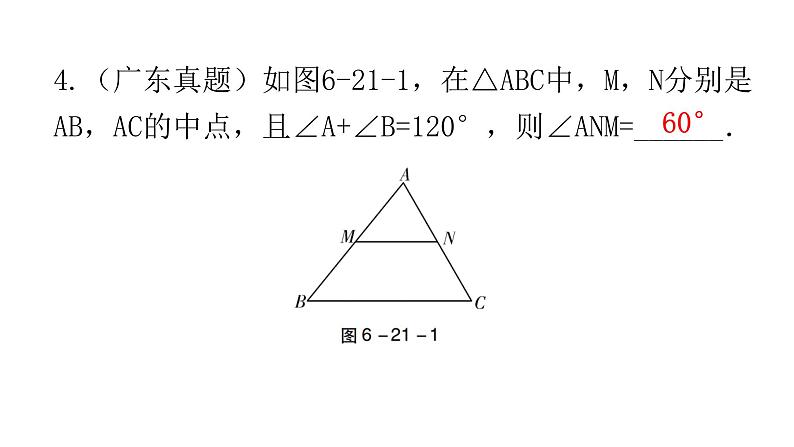
4.（广东真题）如图6-21-1，在△ABC中，M，N分别是AB，AC的中点，且∠A+∠B=120°，则∠ANM=______．
5.（广东真题）如图6-21-2，已知AB是⊙O的直径，BC为弦，∠ABC＝30°.过圆心O作OD⊥BC交⊙O于点D，连接DC，则∠DCB＝________.
①理解圆、弧、弦、圆心角、圆周角的概念，了解等圆、等弧的概念；探索并掌握点与圆的位置关系.②探索并证明垂径定理：垂直于弦的直径平分弦以及弦所对的两条弧.③探索圆周角与圆心角及其所对弧的关系，知道同弧（或等弧）所对的圆周角相等（新增）.了解并证明圆周角定理及其推论：圆周角等于它所对弧上的圆心角的一半；直径所对的圆周角是直角；90°的圆周角所对的弦是直径；圆内接四边形的对角互补.
人教：九上第二十四章 圆北师：九下第三章 圆
1.圆平面上到定点的距离等于定长的所有点组成的图形叫做圆.其中，定点称为_________，定长称为_________
例1.下列条件中，能确定一个圆的是 （ ）A.以点O 为圆心B.以2 cm 长为半径C.以点O 为圆心，5 cm 长为半径D.经过点A
2.圆的对称性（1）圆是轴对称图形，其对称轴是任意一条________的直线，有_______条对称轴.（2）圆是中心对称图形，对称中心为___________
例2.下列图形中对称轴最多是 （ ）A.圆B.正方形C.角D.线段
3.与圆有关的概念（1）弧：圆上任意_______的部分叫做圆弧，简称弧.（2）弦：连接圆上任意两点的_______叫做弦.（3）直径：经过_______的弦叫做直径.（4）圆心角：顶点在_______的角叫做圆心角.（5）圆周角：顶点在_______，两边分别与圆还有另一个交点.像这样的角，叫做圆周角
例3.已知⊙O的半径是6 cm，则⊙O中最长的弦长是（ ）A.6 cmB.12 cmC.16 cmD.20 cm
4.圆心角、弧、弦之间的关系（1）在同圆或等圆中，相等的圆心角所对的弧_______，所对的弦________.（2）在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别________
例4.如图6-21-3，AB，CD 是 ⊙O 的两条弦，OE⊥AB 于点 E，OF⊥CD 于点 F.如果 AB=CD，那么下列结论中错误的是 （ ） A.AB=CDB.∠AOB=∠CODC.OE=OFD.∠AOC=∠BOD
5.垂径定理及其推论（1）垂径定理：垂直于弦的直径___________这条弦，并且___________弦所对的弧.（2）推论：①平分弦（不是直径）的直径_________于弦，并且___________弦所对的弧；
②弦的垂直平分线经过_________，并且平分弦所对的两条弧；③平分弦所对的一条弧的直径___________弦，并且_________弦所对的另一条弧
6.圆周角定理及其推论（1）定理：圆周角的度数等于它所对弧上的圆心角度数的_________.（2）推论：①同弧或等弧所对的圆周角_________；②半圆（或直径）所对的圆周角是__________，90°的圆周角所对的弦是___________；③圆内接四边形的对角___________
例6.（1）如图6-21-5，AB 为 ⊙O 的直径，点 C 在 ⊙O 上，若 ∠ACO=50°，则 ∠B 的度数为 （ ） A.60°B.50°C.40°D.30°
（2）如图6-21-6，四边形 ABCD 内接于 ⊙O，E 为 DC 延长线上一点，∠A=50°，则∠BCE 的度数 （ ）A.40°B.50°C.60°D.130°
1.（2022·威海）如图6-21-9，四边形ABCD是⊙O的内接四边形，连接AC，BD，延长CD至点E.（1）若AB＝AC，求证：∠ADB＝∠ADE；（2）若BC＝3，⊙O的半径为2，求sin∠BAC.
（1）证明：∵四边形ABCD是⊙O的内接四边形，∴∠ADC+∠ABC=180°．···1分（利用圆内接四边形的性质得1分）又∵∠ADC+∠ADE=180°，∴∠ADE＝∠ABC．············2分（等量代换得1分）∵AB＝AC，∴∠ABC＝∠ACB.··········3分（利用等边对等角得1分）又∵∠ACB＝∠ADB，··4分（利用“同弧所对的圆周角相等”得1分）∴∠ADB＝∠ADE.··············5分（等量代换得1分）
（2）解：如图6-21-10，连接CO并延长交⊙O于点F，连接BF.········6分（作辅助线得1分）∵CF为⊙O的直径，∴∠FBC=90°．·····7分（利用“直径所对的圆周角是直角”得1分）∵⊙O的半径为2，∴CF=2×2=4．········8分（利用直径的性质得1分）
温馨提示：此类考题常见于广东省中考数学试卷的第22小题，分值一般为12分，答题时要注意书写格式，分步书写，慢做会求全对，评卷老师是分步给分的哦！
【典型错例】分类讨论在圆周角中的应用
2.已知⊙O是△ABC的外接圆，过顶点A，B分别作⊙O的切线，它们交于点P，若∠APB＝50°，求∠ACB的度数.
【变式考点】圆的有关概念及其基础应用
【创新考点】圆的基础知识的创新应用
4.（2022·娄底）如图6-21-13，以BC为边分别作菱形BCDE和菱形BCFG（点C，D，F共线），动点A在以BC为直径且处于菱形BCFG内的圆弧上，连接EF交BC于点O.设∠G＝θ.（1）求证：无论θ为何值，EF与BC互相平分；并请直接写出使EF⊥BC成立的θ值； （2）当θ＝90°时，试给出tan∠ABC的值，使得EF垂直平分AC，请说明理由.
一、选择题1.（2022·嘉兴）如图6-21-14，在⊙O中，点A在BAC上，若∠BOC＝130°，则∠BAC的度数为（ ）A.55°B.65°C.75°D.130°
2.（2022·兰州）如图6-21-15，△ABC内接于⊙O，CD是⊙O的直径，∠ACD＝40°，则∠B＝（ ）A.70°B.60°C.50°D.40°
3.（2022·自贡）如图6-21-16，四边形ABCD内接于⊙O，AB是⊙O的直径，∠ABD＝20°，则∠BCD的度数是（ ）A.90°B.100°C.110°D.120°
二、填空题6.（2022·甘肃）如图6-21-19，⊙O是四边形ABCD的外接圆，若∠ABC＝110°，则∠ADC＝________°.
7.（2022·永州）如图6-21-20，AB是⊙O的直径，点C，D在⊙O上，∠ADC＝30°，则∠BOC＝_________°.
8.（2022·黑龙江）如图6-21-21，在⊙O中，AB是⊙O的弦，⊙O的半径为3 cm.C为⊙O上一点，∠ACB＝60°，则AB的长为_________cm.
三、解答题9.（2022·怀化）如图6-21-22，点A，B，C，D在⊙O上，AB=CD.求证：（1）AC＝BD；（2）△ABE∽△DCE.
解：（1）△BDE是等腰直角三角形.证明如下：∵AE 平分∠BAC，BE 平分∠ABC，∴∠BAE＝∠CAD＝∠CBD，∠ABE＝∠CBE.∵∠BED＝∠BAE+∠ABE，∠DBE＝∠CBD+∠CBE，∴∠BED＝∠DBE.∴ED=BD.∵AB为⊙O的直径，∴∠ADB＝90°.∴△BDE是等腰直角三角形.
（2022·湖北，几何直观；运算能力；推理能力）如图6-21-24，正方形ABCD内接于⊙O，E为AB的中点，连接CE交BD于点F，延长CE交⊙O于点G，连接BG.（1）求证：FB2＝FE·FG；（2）若AB＝6，求FB和EG的长.