中考数学复习微专题八动点问题（点动、线动、形动）模型四形动课件

这是一份中考数学复习微专题八动点问题（点动、线动、形动）模型四形动课件，共14页。PPT课件主要包含了基本模型，针对训练，针对巩固等内容，欢迎下载使用。

“形动型问题”是指题设图形中存在一个或多个动图,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是化动为静，并利用好特殊图形的性质、函数的性质等.
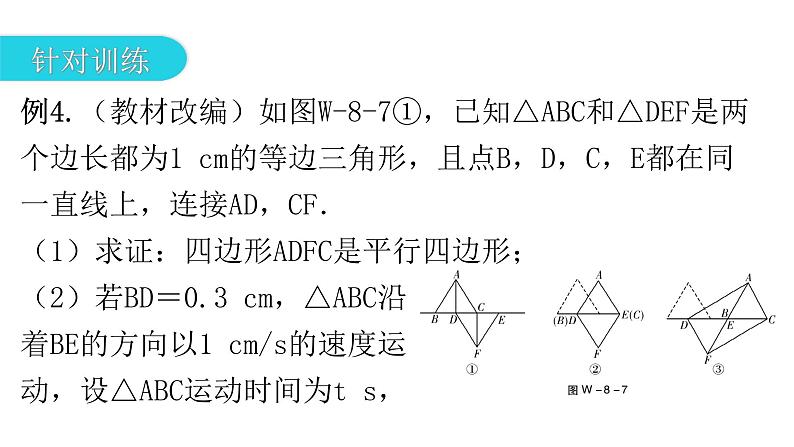
例4.（教材改编）如图W-8-7①，已知△ABC和△DEF是两个边长都为1 cm的等边三角形，且点B，D，C，E都在同一直线上，连接AD，CF．（1）求证：四边形ADFC是平行四边形；（2）若BD＝0.3 cm，△ABC沿着BE的方向以1 cm/s的速度运动，设△ABC运动时间为t s，
①如图W-8-7②，当t为何值时，□ADFC是菱形？请说明你的理由；②如图W-8-7③，□ADFC有可能是矩形吗？若可能，求出t的值及此矩形的面积；若不可能，请说明理由．
（1）证明：∵△ABC和△DEF是两个边长都为1 cm的等边三角形，∴AC＝DF＝1 cm，∠ACB＝∠FDE＝60°.∴AC∥DF.∴四边形ADFC是平行四边形.
（2）解：①当t＝0.3时，□ADFC是菱形.理由如下：∵△ABC沿着BE的方向以1 cm/s的速度运动，BD=0.3 cm,∴当t=0.3时，点B与点D重合，点C与点E重合.则AD＝AC＝DE＝DF＝FC.∴□ADFC是菱形.②□ADFC有可能是矩形.若□ADFC是矩形，则∠ADF＝90°.∴∠ADC＝90°-∠EDF＝30°.同理∠DAB＝30°＝∠ADC.
4.（教材改编）如图W-8-8，正方形ABCD的边长为3 cm，在Rt△EFG中，∠EGF＝90°，FG＝8 cm，EG＝6 cm，点B，C，E，G在直线l上，正方形ABCD由C，E重合的位置开始，以1 cm/s的速度沿直线l按箭头所表示的方向做匀速直线运动．
（1）当正方形ABCD运动时，分别求点D,A运动到EF上的时间；（2）设经过x s后，正方形ABCD与△EFG重叠部分的面积为y cm2，求y与x的函数关系式，并求出自变量x的取值范围．