





2024届高考数学一轮复习(新教材人教A版强基版)第七章立体几何与空间向量7.3空间点、直线、平面之间的位置关系课件
展开1.借助长方体,在直观认识空间点、直线、平面的位置关系的基础上,抽象出空间点、 直线、平面的位置关系的定义.2.了解四个基本事实和一个定理,并能应用定理解决问题.
1.基本事实1:过_______________的三个点,有且只有一个平面.基本事实2:如果一条直线上的_______在一个平面内,那么这条直线在这个平面内.基本事实3:如果两个不重合的平面有一个公共点,那么它们有且只有_____过该点的公共直线.基本事实4:平行于同一条直线的两条直线______.
2.“三个”推论推论1:经过一条直线和这条直线外一点,有且只有一个平面.推论2:经过两条______直线,有且只有一个平面.推论3:经过两条______直线,有且只有一个平面.3.空间中直线与直线的位置关系
_____直线:在同一平面内,有且只有一个公共点;_____直线:在同一平面内,没有公共点;
异面直线:不同在_____一个平面内,没有公共点.
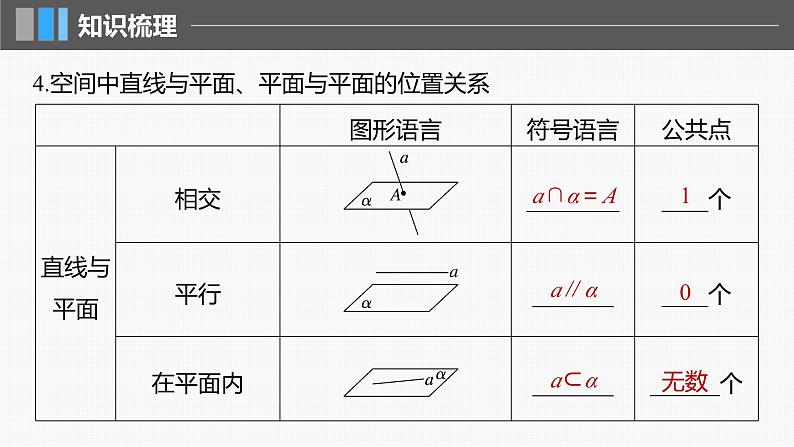
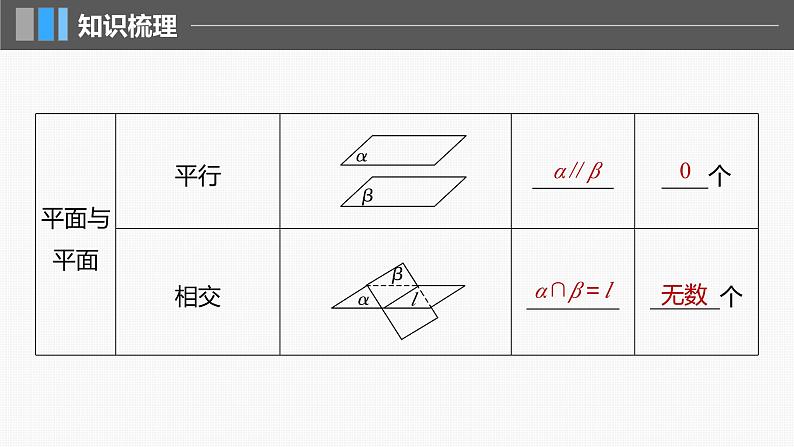
4.空间中直线与平面、平面与平面的位置关系
5.等角定理如果空间中两个角的两条边分别对应平行,那么这两个角___________.6.异面直线所成的角(1)定义:已知两条异面直线a,b,经过空间任一点O分别作直线a′∥a,b′∥b,我们把直线a′与b′所成的角叫做异面直线a与b所成的角(或夹角).(2)范围:______.
1.过平面外一点和平面内一点的直线,与平面内不过该点的直线是异面直线.2.分别在两个平行平面内的直线平行或异面.
判断下列结论是否正确(请在括号中打“√”或“×”)(1)没有公共点的两条直线是异面直线.( )(2)直线与平面的位置关系有平行、垂直两种.( )(3)如果两个平面有三个公共点,则这两个平面重合.( )(4)两两相交的三条直线共面.( )
1.(多选)如图是某正方体的平面展开图,则在这个正方体中,下列说法正确的是A.BM与ED平行B.CN与BM成60°角C.CN与BE是异面直线D.DM与BN是异面直线
正方体的直观图如图所示.很显然,BM与ED不平行,故A错误;连接AN,AC,易知△ACN是等边三角形,CN与BM所成角即为∠ANC=60°,故B正确;连接BE,易知CN∥BE,故C错误;连接BN,DM,易知DM与BN是异面直线,故D正确.
2.已知a,b是异面直线,直线c平行于直线a,那么c与bA.一定是异面直线B.一定是相交直线C.不可能是平行直线D.不可能是相交直线
由已知得直线c与b可能为异面直线也可能为相交直线,但不可能为平行直线,若b∥c,则a∥b,与已知a,b为异面直线相矛盾.
3.如图,在三棱锥A-BCD中,E,F,G,H分别是棱AB,BC,CD,DA的中点,则(1)当AC,BD满足条件________时,四边形EFGH为菱形;
∴四边形EFGH为平行四边形,∵四边形EFGH为菱形,∴EF=EH,∴AC=BD.
(2)当AC,BD满足条件__________________时,四边形EFGH为正方形.
AC=BD且AC⊥BD
∵四边形EFGH为正方形,∴EF=EH且EF⊥EH,∴AC=BD且AC⊥BD.
例1 已知在正方体ABCD-A1B1C1D1中,E,F分别为D1C1,C1B1的中点,AC∩BD=P,A1C1∩EF=Q.求证:(1)D,B,F,E四点共面;
(2)若A1C交平面DBFE于点R,则P,Q,R三点共线;
(3)DE,BF,CC1三线交于一点.
共面、共线、共点问题的证明(1)共面:先确定一个平面,然后再证其余的线(或点)在这个平面内.(2)共线:先由两点确定一条直线,再证其他各点都在这条直线上.(3)共点:先证其中两条直线交于一点,再证其他直线经过该点.
跟踪训练1 (1)如图,α∩β=l,A,B∈α,C∈β,且A,B,C∉l,直线AB∩l=M,过A,B,C三点的平面记作γ,则γ与β的交线必经过A.点AB.点BC.点C但不过点MD.点C和点M
①证明:四边形BCHG是平行四边形;
故GH∥BC且GH=BC,所以四边形BCHG是平行四边形.
②C,D,F,E四点是否共面?为什么?
命题点1 空间位置关系的判断例2 (1)(多选)下列推断中,正确的是A.M∈α,M∈β,α∩β=l⇒M∈lB.A∈α,A∈β,B∈α,B∈β⇒α∩β=ABC.l⊄α,A∈l⇒A∉αD.A,B,C∈α,A,B,C∈β,且A,B,C不共线⇒α,β重合
(2)(2023·龙岩模拟)若a和b是异面直线,b和c是异面直线,则a和c的位置关系是A.异面或平行 B.异面或相交C.异面 D.相交、平行或异面
命题点2 异面直线所成的角例3 (1)如图,圆柱的轴截面ABCD为正方形,E为弧BC的中点,则异面直线AE与BC所成角的余弦值为
如图,过点E作圆柱的母线交下底面于点F,
(2)(2022·长春模拟)在正方体ABCD-A1B1C1D1中,P,Q分别为BC,A1B1的中点,则异面直线PQ与A1C1所成角的正弦值为
(1)点、直线、平面位置关系的判定,注意构造几何体(长方体、正方体)模型来判断,常借助正方体为模型.(2)求异面直线所成角的方法
跟踪训练2 (1)(多选)如图所示,在正方体ABCD-A1B1C1D1中,M,N分别为棱C1D1,C1C的中点,以下四个选项正确的是A.直线AM与CC1是相交直线B.直线AM与BN是平行直线C.直线BN与MB1是异面直线D.直线AM与DD1是异面直线
由题意,EF∥E1F1,则∠AE1F1即为所求.
(3)平面α过正方体ABCD-A1B1C1D1的顶点A,α∥平面CB1D1,α∩平面ABCD=m,α∩平面ABB1A1=n,则m,n所成角的正弦值为
例4 (1)正方体ABCD-A1B1C1D1中,P,Q,E,F分别是AB,AD,B1C1,C1D1的中点,则正方体过P,Q,E,F的截面图形的形状是A.正方形 B.平行四边形C.正五边形 D.正六边形
空间几何体的切割(截面)问题
(2)如图,圆锥VO的母线长为l,轴截面VAB的顶角∠AVB=150°,则过此圆锥的顶点作该圆锥的任意截面VCD,则△VCD面积的最大值是_____,此时∠VCD=_____.
(1)作截面应遵循的三个原则:①在同一平面上的两点可引直线;②凡是相交的直线都要画出它们的交点;③凡是相交的平面都要画出它们的交线.(2)作交线的方法有如下两种:①利用基本事实3作交线;②利用线面平行及面面平行的性质定理去寻找线面平行及面面平行,然后根据性质作出交线.
跟踪训练3 (1)(多选)在正方体ABCD-A1B1C1D1中,E,F分别在B1B和C1C上(异于端点),则过三点A,F,E的平面被正方体截得的图形(截面)可能是A.矩形 B.菱形 C.正方形 D.梯形
(2)如图,在正方体ABCD-A1B1C1D1中,E是BC的中点,平面α经过直线BD且与直线C1E平行,若正方体的棱长为2,则平面α截正方体所得的多边形的面积为_____.
1.若直线上有两个点在平面外,则A.直线上至少有一个点在平面内B.直线上有无穷多个点在平面内C.直线上所有点都在平面外D.直线上至多有一个点在平面内
2.(多选)如图是正方体或四面体,P,Q,R,S分别是所在棱的中点,这四个点共面的图形是
在A中分别连接PS,QR,易证PS∥QR,所以P,Q,R,S四点共面;在B中过点P,Q,R,S可作一正六边形,故四点共面;在C中分别连接PQ,RS,易证PQ∥RS,所以P,Q,R,S共面;在D中PS与QR为异面直线,所以四点不共面.
3.已知α,β,γ是平面,a,b,c是直线,α∩β=a,β∩γ=b,γ∩α=c,若a∩b=P,则A.P∈c B.P∉cC.c∩a=∅ D.c∩β=∅
4.在底面半径为1的圆柱OO1中,过旋转轴OO1作圆柱的轴截面ABCD,其中母线AB=2,E是 的中点,F是AB的中点,则A.AE=CF,AC与EF是共面直线B.AE≠CF,AC与EF是共面直线C.AE=CF,AC与EF是异面直线D.AE≠CF,AC与EF是异面直线
5.(多选)用一个平面截正方体,截面可能出现的形状是A.等边三角形 B.直角梯形C.菱形 D.五边形
6.(2021·全国乙卷)在正方体ABCD-A1B1C1D1中,P为B1D1的中点,则直线PB与AD1所成的角为
7.如图为正方体表面的一种展开图,则图中的AB,CD,EF,GH在原正方体中互为异面直线的有____对.
8.如图是某机械零件的几何结构,该几何体是由两个相同的直四棱柱组合而成的,且前后、左右、上下均对称,每个四棱柱的底面都是边长为2的正方形,高为4,且两个四棱柱的侧棱互相垂直.则这两个四棱柱的表面相交的交线段总长度为______.
9.如图所示,在空间四边形ABCD中,E,F分别是AB,AD的中点,G,H分别在BC,CD上,且BG∶GC=DH∶HC=1∶2.
(1)求证:E,F,G,H四点共面;
(2)设EG与FH交于点P,求证:P,A,C三点共线.
(1)三棱锥P-ABC的体积;
(2)异面直线BC与AD所成角的余弦值.
如图,取PB的中点E,连接DE,AE,则ED∥BC,所以∠ADE是异面直线BC与AD所成的角(或其补角).
12.如图,E,F分别为正方体ABCD-A1B1C1D1的棱CC1,C1D1的中点,若AB=6,则过A,E,F三点的截面的面积为
连接EF,作直线EF分别与直线DC,DD1的延长线相交于点P,Q,连接AP交BC于点M,连接AQ交A1D1于点N,连接NF,ME.则五边形AMEFN即为过A,E,F三点的截面,如图所示.
在平面ABD中,过E作EG∥AB,交DB于点G,连接GF,如图,
则GF∥CD,∴∠EGF(或其补角)即为AB与CD所成角,
∴∠EGF=120°,∴AB与CD所成角的大小为60°.
(1)球O的表面积为_____;
(2)若D是BC的中点,过点D作球O的截面,则截面面积的最小值是_____.
如图,连接BD,A1D,过点P作BD,A1D的平行线,分别交棱AB,AA1于点Q,R,连接QR,因为BD∥B1D1,所以PQ∥B1D1,因为B1D1⊂平面B1D1C,PQ⊄平面B1D1C,所以PQ∥平面B1D1C,
因为A1D∥B1C,所以PR∥B1C,因为B1C⊂平面B1D1C,PR⊄平面B1D1C,所以PR∥平面B1D1C,又PQ∩PR=P,PQ,PR⊂平面PQR,所以平面PQR∥平面B1D1C,则△PQR为截面,
16.如图,在四棱锥P-ABCD中,PC⊥底面ABCD,ABCD是直角梯形,AD⊥DC,AB∥DC,AB=2AD=2CD=2,点E是PB的中点.
(1)线段PA上是否存在一点G,使得点D,C,E,G共面?若存在,请证明,若不存在,请说明理由;
存在.当G为PA的中点时满足条件.如图,连接GE,GD,则GE是△PAB的中位线,所以GE∥AB.又AB∥DC,所以GE∥DC,所以G,E,C,D四点共面.
(2)若PC=2,求三棱锥P-ACE的体积.
2024届高考数学一轮复习(新教材人教A版强基版)第七章立体几何与空间向量7.6空间向量的概念与运算课件: 这是一份2024届高考数学一轮复习(新教材人教A版强基版)第七章立体几何与空间向量7.6空间向量的概念与运算课件,共60页。PPT课件主要包含了落实主干知识,探究核心题型,课时精练,同一个平面,a=λb,xa+yb,xa+yb+zc,-12,同理可排除CD,VA∥平面PMN等内容,欢迎下载使用。
2024届高考数学一轮复习(新教材人教A版强基版)第七章立体几何与空间向量7.5空间直线、平面的垂直课件: 这是一份2024届高考数学一轮复习(新教材人教A版强基版)第七章立体几何与空间向量7.5空间直线、平面的垂直课件,共60页。PPT课件主要包含了落实主干知识,探究核心题型,课时精练,任意一条,m⊂α,n⊂α,m∩n=P,两条相交直,l⊥m,l⊥n等内容,欢迎下载使用。
2024届高考数学一轮复习(新教材人教A版强基版)第七章立体几何与空间向量7.2球的切、接问题课件: 这是一份2024届高考数学一轮复习(新教材人教A版强基版)第七章立体几何与空间向量7.2球的切、接问题课件,共60页。PPT课件主要包含了题型一,定义法,思维升华,题型二,补形法,题型三,截面法,课时精练,第三部分,设正方体的棱长为a等内容,欢迎下载使用。












