2024届高考数学一轮复习（新教材人教A版强基版）第七章立体几何与空间向量7.5空间直线、平面的垂直课件

这是一份2024届高考数学一轮复习（新教材人教A版强基版）第七章立体几何与空间向量7.5空间直线、平面的垂直课件，共60页。PPT课件主要包含了落实主干知识，探究核心题型，课时精练，任意一条，m⊂α，n⊂α，m∩n＝P，两条相交直，l⊥m，l⊥n等内容，欢迎下载使用。

1.理解空间中直线与直线、直线与平面、平面与平面的垂直关系.2.掌握直线与平面、平面与平面垂直的判定与性质，并会简单应用.
1.直线与平面垂直(1)直线和平面垂直的定义一般地，如果直线l与平面α内的_________直线都垂直，就说直线l与平面α互相垂直.
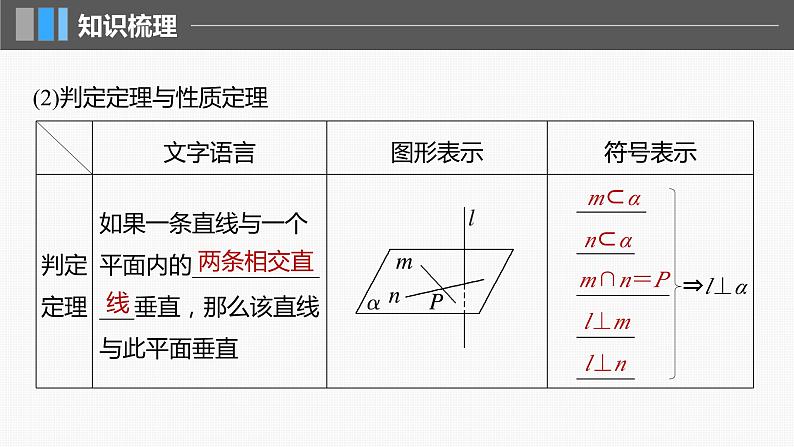
(2)判定定理与性质定理
_____________________________
2.直线和平面所成的角(1)定义：平面的一条斜线和它在平面上的______所成的角，叫做这条直线和这个平面所成的角.一条直线垂直于平面，我们说它们所成的角是_____；一条直线和平面平行，或在平面内，我们说它们所成的角是____.
(2)范围：______.
3.二面角(1)定义：从一条直线出发的____________所组成的图形叫做二面角.(2)二面角的平面角：如图，在二面角α－l－β的棱l上任取一点O，以点O为垂足，在半平面α和β内分别作__________的射线OA和OB，则射线OA和OB构成的∠AOB叫做二面角的平面角.(3)二面角的范围：________.
4.平面与平面垂直(1)平面与平面垂直的定义一般地，两个平面相交，如果它们所成的二面角是_________，就说这两个平面互相垂直.
_______________________
1.三垂线定理平面内的一条直线如果和穿过这个平面的一条斜线在这个平面内的射影垂直，那么它也和这条斜线垂直.2.三垂线定理的逆定理平面内的一条直线如果和穿过该平面的一条斜线垂直，那么它也和这条斜线在该平面内的射影垂直.3.两个相交平面同时垂直于第三个平面，它们的交线也垂直于第三个平面.
判断下列结论是否正确(请在括号中打“√”或“×”)(1)若直线l与平面α内的两条直线都垂直，则l⊥α.(　 　)(2)若直线a⊥α，b⊥α，则a∥b.(　 　)(3)若两平面垂直，则其中一个平面内的任意一条直线垂直于另一个平面.(　 　)(4)若α⊥β，a⊥β，则a∥α.(　 　)
1.(多选)下列命题中不正确的是A.如果直线a不垂直于平面α，那么平面α内一定不存在直线垂直于直线aB.如果平面α垂直于平面β，那么平面α内一定不存在直线平行于平面βC.如果直线a垂直于平面α，那么平面α内一定不存在直线平行于直线aD.如果平面α⊥平面β，那么平面α内所有直线都垂直于平面β
若直线a垂直于平面α，则直线a垂直于平面α内的所有直线，故C正确，其他选项均不正确.
2.如图，在正方形SG1G2G3中，E，F分别是G1G2，G2G3的中点，D是EF的中点，现在沿SE，SF及EF把这个正方形折成一个四面体，使G1，G2，G3三点重合，重合后的点记为G，则在四面体S－EFG中必有A.SG⊥△EFG所在平面B.SD⊥△EFG所在平面C.GF⊥△SEF所在平面D.GD⊥△SEF所在平面
四面体S－EFG如图所示，由SG⊥GE，SG⊥GF，GE∩GF＝G且GE，GF⊂平面EFG得SG⊥△EFG所在平面.
3.已知PD垂直于正方形ABCD所在的平面，连接PB，PC，PA，AC，BD，则一定互相垂直的平面有____对.
如图，由于PD垂直于正方形ABCD，故平面PDA⊥平面ABCD，平面PDB⊥平面ABCD，平面PDC⊥平面ABCD，平面PDA⊥平面PDC，平面PAC⊥平面PDB，平面PAB⊥平面PAD，平面PBC⊥平面PDC，共7对.
例1　(1)已知l，m是平面α外的两条不同直线.给出下列三个论断：①l⊥m；②m∥α；③l⊥α.以其中的两个论断作为条件，余下的一个论断作为结论，写出一个正确的命题_____________________.
直线与平面垂直的判定与性质
②③⇒①(或①③⇒②)
已知l，m是平面α外的两条不同直线，由①l⊥m与②m∥α，不能推出③l⊥α，因为l可以与α平行，也可以相交不垂直；由①l⊥m与③l⊥α能推出②m∥α；由②m∥α与③l⊥α可以推出①l⊥m.
(2)(2023·娄底模拟)如图，在三棱柱ABC－A1B1C1中，点B1在底面ABC内的射影恰好是点C.①若点D是AC的中点，且DA＝DB，证明：AB⊥CC1.
证明线面垂直的常用方法及关键(1)证明直线和平面垂直的常用方法：①判定定理；②垂直于平面的传递性(a∥b，a⊥α⇒b⊥α)；③面面平行的性质(a⊥α，α∥β⇒a⊥β)；④面面垂直的性质.(2)证明线面垂直的关键是证线线垂直，而证明线线垂直则需借助线面垂直的性质.
跟踪训练1　如图，在正方体ABCD－A1B1C1D1中，E，F分别是棱CD，A1D1的中点.(1)求证：AB1⊥BF；
(2)求证：AE⊥BF；
存在.如图，取棱CC1的中点P，即为所求.连接EP，AP，C1D，因为EP∥C1D，C1D∥AB1，所以EP∥AB1.由(1)知AB1⊥BF，所以BF⊥EP.又由(2)知AE⊥BF，且AE∩EP＝E，所以BF⊥平面AEP.
(3)棱CC1上是否存在点P，使BF⊥平面AEP？若存在，确定点P的位置，若不存在，说明理由.
例2　(2023·桂林模拟)如图所示，已知在四棱锥P－ABCD中，底面ABCD是矩形，平面PAD⊥底面ABCD且AB＝1，PA＝AD＝PD＝2，E为PD的中点.
平面与平面垂直的判定与性质
(1)求证：平面PCD⊥平面ACE；
(2)求点B到平面ACE的距离.
(1)判定面面垂直的方法①面面垂直的定义.②面面垂直的判定定理.(2)面面垂直性质的应用①面面垂直的性质定理是把面面垂直转化为线面垂直的依据，运用时要注意“平面内的直线”.②若两个相交平面同时垂直于第三个平面，则它们的交线也垂直于第三个平面.
跟踪训练2　(2022·邯郸模拟)如图，在四棱锥P－ABCD中，AB∥CD，AB⊥AD，CD＝2AB，平面PAD⊥平面ABCD，PA⊥AD，E和F分别是CD和PC的中点，求证：(1)PA⊥平面ABCD；
(2)平面BEF∥平面PAD；
(3)平面BEF⊥平面PCD.
例3　如图，已知ABCD－A1B1C1D1是底面为正方形的长方体，∠AD1A1＝60°，AD1＝4，点P是AD1上的动点.(1)试判断不论点P在AD1上的任何位置，是否都有平面BPA⊥平面AA1D1D，并证明你的结论；
(2)当P为AD1的中点时，求异面直线AA1与B1P所成的角的余弦值；
(3)求PB1与平面AA1D1D所成的角的正切值的最大值.
(1)三种垂直的综合问题，一般通过作辅助线进行线线、线面、面面垂直间的转化.(2)对于线面关系中的存在性问题，首先假设存在，然后在该假设条件下，利用线面关系的相关定理、性质进行推理论证.
(1)证明：PO⊥平面ABC；
1.(多选)若平面α，β满足α⊥β，α∩β＝l，P∈α，P∉l，则下列命题中是真命题的为A.过点P垂直于平面α的直线平行于平面βB.过点P垂直于直线l的直线在平面α内C.过点P垂直于平面β的直线在平面α内D.过点P且在平面α内垂直于l的直线必垂直于平面β
2.如图，已知AB是圆柱上底面的一条直径，C是上底面圆周上异于A，B的一点，D为下底面圆周上一点，且AD⊥圆柱的底面，则必有A.平面ABC⊥平面BCDB.平面BCD⊥平面ACDC.平面ABD⊥平面ACDD.平面BCD⊥平面ABD
3.如图，在斜三棱柱ABC－A1B1C1中，∠BAC＝90°，BC1⊥AC，则C1在底面ABC上的射影H必在A.直线AB上B.直线BC上C.直线AC上D.△ABC内部
4.(多选)如图，在以下四个正方体中，直线AB与平面CDE垂直的是
5.(多选)(2023·新乡模拟)设m，n是两条不同的直线，α，β是两个不重合的平面，则下列命题正确的是A.若m⊥n，n⊂α，则m⊥αB.若m⊥α，m⊂β，则α⊥βC.若m⊥α，n⊥α，则m∥nD.若m⊂α，n⊂β，α∥β，则m∥n
6.(多选)(2022·新高考全国Ⅰ)已知正方体ABCD－A1B1C1D1，则A.直线BC1与DA1所成的角为90°B.直线BC1与CA1所成的角为90°C.直线BC1与平面BB1D1D所成的角为45°D.直线BC1与平面ABCD所成的角为45°
因为C1C⊥平面ABCD，所以∠CBC1为直线BC1与平面ABCD所成的角，易得∠CBC1＝45°，故D正确.
7.如图所示，在四棱锥P－ABCD中，PA⊥底面ABCD，且底面各边都相等，M是PC上的一动点，当点M满足条件：①BM⊥DM，②DM⊥PC，③BM⊥PC中的________时，平面MBD⊥平面PCD(只要填写一个你认为是正确的条件序号即可).
8.在矩形ABCD中，AB②假设AB⊥CD，∵AB⊥AD，CD∩AD＝D，∴AB⊥平面ACD，∴AB⊥AC，由AB③假设AD⊥BC，∵CD⊥BC，AD∩CD＝D，∴BC⊥平面ACD，∴BC⊥AC，即△ABC为直角三角形，且AB为斜边，而AB9.如图，在四边形ABCD中，AD∥BC，AD＝AB，∠BCD＝45°，∠BAD＝90°.将△ABD沿对角线BD折起，记折起后点A的位置为点P，且使平面PBD⊥平面BCD.求证：(1)CD⊥平面PBD；
(2)平面PBC⊥平面PCD.
10.(2023·广州模拟)如图，在三棱锥P－ABC中，平面PAC⊥平面PBC，PA⊥平面ABC.
(1)求证：BC⊥平面PAC；
(2)若AC＝BC＝PA，求二面角A－PB－C的平面角的大小.
11.如图，正三角形PAD所在平面与正方形ABCD所在平面互相垂直，O为正方形ABCD的中心，M为正方形ABCD内一点，且满足MP＝MC，则点M的轨迹为
A.该多面体是四棱锥B.平面BAD⊥平面BCDC.平面BAC⊥平面ACD
由题意得该多面体是一个三棱锥，故A错误；∵AP⊥BP，AP⊥CP，BP∩CP＝P，∴AP⊥平面BCD.又∵AP⊂平面BAD，∴平面BAD⊥平面BCD，故B正确；同理可证平面BAC⊥平面ACD，故C正确；
13.(多选)如图，在正方体ABCD－A1B1C1D1中，点P在线段B1C上运动，则下列说法正确的是A.直线BD1⊥平面A1C1DB.三棱锥P－A1C1D的体积为定值
15.刘徽注《九章算术·商功》“斜解立方，得两堑堵.斜解堑堵，其一为阳马，一为鳖臑.阳马居二，鳖臑居一，不易之率也.合两鳖臑三而一，验之以棊，其形露矣.”如图1解释了由一个长方体得到“堑堵”“阳马”“鳖臑”的过程.堑堵是底面为直角三角形的直棱柱；阳马是一条侧棱垂直于底面且底面为矩形的四棱锥；鳖臑是四个面都为直角三角形的四面体.
在如图2所示由正方体ABCD－A1B1C1D1得到的堑堵ABC－A1B1C1中，当点P在下列三个位置：A1A中点，A1B中点，A1C中点时，分别形成的四面体P－ABC中，鳖臑的个数为A.0 B.1 C.2 D.3
16.在长方体ABCD－A1B1C1D1中，已知AB＝2，BC＝t，若在线段AB上存在点E，使得EC1⊥ED，则实数t的取值范围是 ______.