
广东省深圳市福田区红岭教育集团2023-2024学年九年级上学期 开学考数学试卷
展开福田区红岭教育集团2023-2024学年第一学期九年级开学考数学试卷
一.选择题(每题3分,共30分)
1. 下列新能源汽车标志图案中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
2. 下列等式从左到右的变形,是因式分解的是( )
A.x2-4x+4=x(x-4)+4 B.(x+1)2=x2+2x+1
C.x2-4=(x+2)(x-2) D.15x5=3x2•5x3
3. 用配方法解方程x2-4x-10=0,下列配方结果正确的是( )
A.(x+2)2=14 B.(x+2)2=6 C.(x-2)2=14 D.(x-2)2=6
4. 一元二次方程-x2+2x-1=0的根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.只有一个实数根 D.没有实数根
5. 一次函数y1=kx+b和y2=2x的图象如图所示,则kx+b≥2x的解集是( )
A.x≥1 B.x≤2 C.x<1 D.x≤1
6. 下列命题是真命题的是( )
A.若a>b,则1-2a>1-2b
B.等腰三角形的角平分线、中线和高重合
C.一组对边平行,另一组对边相等的四边形是平行四边形
D.一个正多边形的内角和为720°,则这个正多边形的一个外角等于60°
7. 某商店需要购进甲乙两种商品,已知甲的进价比乙多50元,分别用2万元进货甲乙两种商品,购买乙的件数比甲多20件,现设乙的进价为x元,则下列方程正确的是( )
A. B.
C. D.
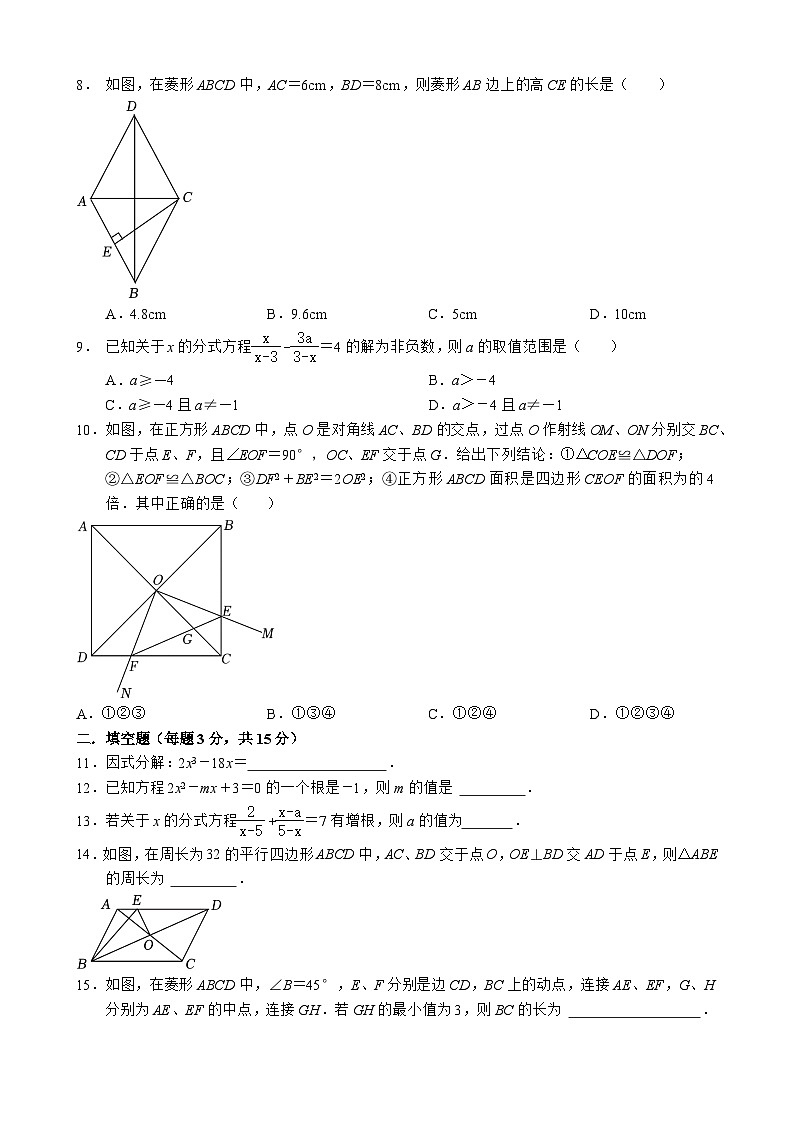
8. 如图,在菱形ABCD中,AC=6cm,BD=8cm,则菱形AB边上的高CE的长是( )
A.4.8cm B.9.6cm C.5cm D.10cm
9. 已知关于x的分式方程=4的解为非负数,则a的取值范围是( )
A.a≥-4 B.a>-4
C.a≥-4且a≠-1 D.a>-4且a≠-1
10.如图,在正方形ABCD中,点O是对角线AC、BD的交点,过点O作射线OM、ON分别交BC、CD于点E、F,且∠EOF=90°,OC、EF交于点G.给出下列结论:①△COE≌△DOF;
②△EOF≌△BOC;③DF2+BE2=2OE2;④正方形ABCD面积是四边形CEOF的面积为的4倍.其中正确的是( )
A.①②③ B.①③④ C.①②④ D.①②③④
二.填空题(每题3分,共15分)
11.因式分解:2x3-18x= .
12.已知方程2x2-mx+3=0的一个根是-1,则m的值是 .
13.若关于x的分式方程=7有增根,则a的值为 .
14.如图,在周长为32的平行四边形ABCD中,AC、BD交于点O,OE⊥BD交AD于点E,则△ABE的周长为 .
15.如图,在菱形ABCD中,∠B=45°,E、F分别是边CD,BC上的动点,连接AE、EF,G、H分别为AE、EF的中点,连接GH.若GH的最小值为3,则BC的长为 .
三.解答题(共55分)
16.(8分)解方程:
(1)(x-1)2=3(x-1); (2)x2-4x+1=0.
17.(8分)(1)解不等式组:并把它的解集在数轴上表示出来.
(2)先化简,再求值:,其中a=-2.
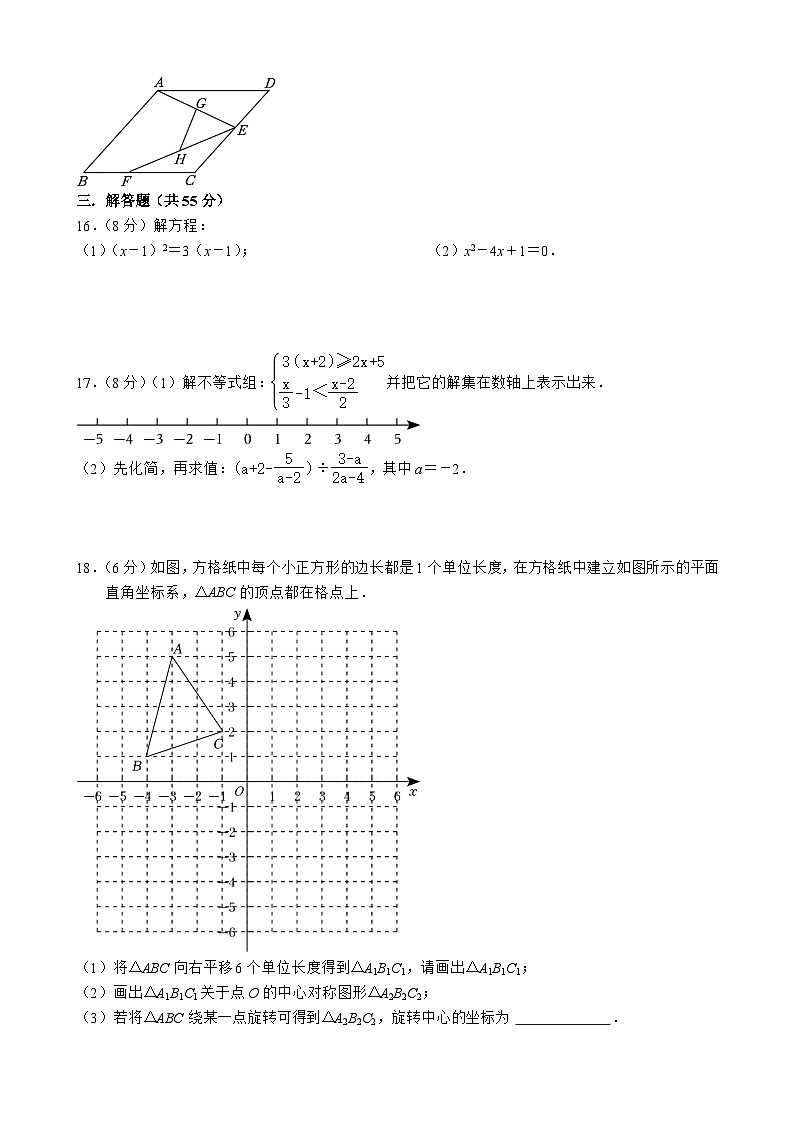
18.(6分)如图,方格纸中每个小正方形的边长都是1个单位长度,在方格纸中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上.
(1)将△ABC向右平移6个单位长度得到△A1B1C1,请画出△A1B1C1;
(2)画出△A1B1C1关于点O的中心对称图形△A2B2C2;
(3)若将△ABC绕某一点旋转可得到△A2B2C2,旋转中心的坐标为 .
19.(8分)如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB,交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形.
(2)若AB=5,BD=6,求OE的长.
20.(8分)某服装店老板用4000元购进了一批甲款T恤,用8800元购进了一批乙款T恤,已知所购乙款T恤数量是甲款T恤数量的2倍,购进的乙款T恤单价比甲款T恤单价贵5元.
(1)购进甲、乙两款T恤的单价分别是多少元?
(2)老板把这两种T恤的标价都定为每件100元,甲款T恤打九折销售,乙款T恤按标价销售.经过一段时间的销售,老板发现,销售两种T恤共100件时,利润不低于4200元.那么这段时间按标价销售的乙款T恤至少要销售多少件?
21.(9分)【问题情境】:如图1,点E为正方形ABCD内一点,AE=2,BE=4,∠AEB=90°,将直角三角形ABE绕点A逆时针方向旋转α度(0≤α≤180°)点B、E的对应点分别为点B′、E′.
【问题解决】:
(1)如图2,在旋转的过程中,点B′落在了AC上,求此时CB′的长;
(2)若α=90°,如图3,得到△ADE′(此时B′与D重合),延长BE交B′E′于点F,
①试判断四边形AEFE′的形状,并说明理由;
②连接CE,求CE的长;
(3)在直角三角形ABE绕点A逆时针方向旋转过程中,直接写出线段CE′长度的取值范围.
22.(8分)问题提出
(1)如图①,在△ABC中,D、E分别是AB和AC的中点,连接DE,则DE与BC的数量关系是 ,位置关系是 ;
问题探究
(2)如图②,在四边形ABCD中,∠BAC=90°,AB=AC=4,CD=4,E为AD中点,连接BE,求BE的最大值;
问题解决
(3)如图③,某小区计划在一片足够大的空地上修建四边形的花园ABCD,其中BC=20米,AD=CD,AD⊥CD,AB∥CD,由于受地理位置的影响,∠ABC<90°.根据要求,现计划给该花园修建条笔直的绿色长廊,且绿色长廊的入口O定为BC的中点,出口定为点D,为了尽可能地提高观赏体验,要求绿色长廊OD最长,试求绿色长廊OD最长为多少米?
红岭教育集团九年级开学考数学试卷参考答案与试题解析
一.选择题(共10小题)
1.下列新能源汽车标志图案中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
【解答】解:A、既是轴对称图形,又是中心对称图形,故A符合题意;
B、D,是轴对称图形,但不是中心对称图形,故B、D不符合题意;
C、不是轴对称图形,是中心对称图形.故C不符合题意.
故选:A.
2.下列等式从左到右的变形,是因式分解的是( )
A.x2-4x+4=x(x-4)+4 B.(x+1)2=x2+2x+1
C.x2-4=(x+2)(x-2) D.15x5=3x2•5x3
【解答】解:A.x2-4x+4=(x-2)2,原题干因式分解错误,故A不符合题意;
B.(x+1)2=x2+2x+1,从左边到右边的变形是整式乘法计算,故B不符合题意;
C.x2-4=(x+2)(x-2),从左边到右边的变形属于因式分解,故C符合题意;
D.15x5不属于多项式,故D不符合题意;
故选:C.
3.用配方法解方程x2-4x-10=0,下列配方结果正确的是( )
A.(x+2)2=14 B.(x+2)2=6 C.(x-2)2=14 D.(x-2)2=6
【解答】解:x2-4x-10=0,
移项,得x2-4x=10,
配方,得x2-4x+4=10+4,
即(x-2)2=14.
故选:C.
4.一元二次方程-x2+2x-1=0的根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.只有一个实数根 D.没有实数根
【解答】解:Δ=b2-4ac=22-4×(-1)×(-1)=0,
∴原方程有两个相等的实数根.
故选:B.
5.一次函数y1=kx+b和y2=2x的图象如图所示,则kx+b≥2x的解集是( )
A.x≥1 B.x≤2 C.x<1 D.x≤1
【解答】解:当x≤1时,kx+b≥2x,
所以不等式kx+b≥2x的解集为x≤1.
故选:D.
6.下列命题是真命题的是( )
A.若a>b,则1-2a>1-2b
B.等腰三角形的角平分线、中线和高重合
C.一组对边平行,另一组对边相等的四边形是平行四边形
D.一个正多边形的内角和为720°,则这个正多边形的一个外角等于60°
【解答】解:若a>b,则1-2a<1-2b,故A是假命题,不符合题意;
等腰三角形的顶角的角平分线、底边上的中线和底边上的高重合,故B是假命题,不符合题意;
一组对边平行且相等的四边形是平行四边形,故C是假命题,不符合题意;
一个正多边形的内角和为720°,则这个正多边形有6条边,它的一个外角等于360°÷6=60°,故D是真命题,符合题意;
故选:D.
7.某商店需要购进甲乙两种商品,已知甲的进价比乙多50元,分别用2万元进货甲乙两种商品,购买乙的件数比甲多20件,现设乙的进价为x元,则下列方程正确的是( )
A. B.
C. D.
【解答】解:设乙的进价为x元,则甲的进价是(x+50)元,
根据题意得,.
故选:C.
8.如图,在菱形ABCD中,AC=6cm,BD=8cm,则菱形AB边上的高CE的长是( )
A.4.8cm B.9.6cm C.5cm D.10cm
【解答】解:对角线AC,BD交于点O,则△ABO为直角三角形
则AO=OC=3.BO=DO=4,
∴AB==5cm,
∴菱形的面积根据边长和高可以计算,根据对角线长也可以计算,
即S=×6cm×8cm=5cm×CE,
∴CE=4.8cm,
故选:A.
9.已知关于x的分式方程=4的解为非负数,则a的取值范围是( )
A.a≥-4 B.a>-4 C.a≥-4且a≠-1 D.a>-4且a≠-1
【解答】解:原分式方程可化为,
方程两边同乘x-3得,x+3a=4(x-3),
去括号得,x+3a=4x-12,
移项得,x-4x=-12-3a,
合并同类项得,-3x=-12-3a,
系数化为1得x=a+4,
∵原分式方程的解为非负数,
∴x≥0,x≠3,
即a+4≥0,a+4≠3,
解得a≥-4且a≠-1,
故选:C.
10.如图,在正方形ABCD中,点O是对角线AC、BD的交点,过点O作射线OM、ON分别交BC、CD于点E、F,且∠EOF=90°,OC、EF交于点G.给出下列结论:
①△COE≌△DOF;
②△EOF≌△BOC;
③DF2+BE2=2OE2;
④正方形ABCD面积是四边形CEOF的面积为的4倍.
其中正确的是( )
A.①②③ B.①③④ C.①②④ D.①②③④
【解答】解:在正方形ABCD中,OC=OD,∠COD=90°,∠ODC=∠OCB=45°,
∵∠EOF=90°,
∴∠COE=∠DOF,
∴△COE≌△DOF(ASA),故①正确;
在正方形ABCD中,OF≠OD即OF≠OB,所以△EOF不全等于△BOC;故②错误;
∵△COE≌△DOF,
∴CE=DF,OE=OF,
∵四边形ABCD为正方形,
∴BC=CD,
∴BE=CF,
在Rt△ECF中,CE2+CF2=EF2,
∵∠FOE=90°,
∴OE2+OF2=EF2,
又∵OE=OF,
∴2OE2=EF2,
∴DF2+BE2=CE2+CF2=2OE2,故③正确;
由①全等可得四边形CEOF的面积与△OCD面积相等,
∴正方形ABCD面积是四边形CEOF的面积为的4倍,故④正确.
综上所述,结论正确的是①③④.
故选:B.
二.填空题(共5小题)
11.因式分解:2x3-18x= 2x(x+3)(x-3) .
【解答】解:2x3-18x
=2x(x2-9)
=2x(x+3)(x-3).
故答案为:2x(x+3)(x-3).
12.已知方程2x2-mx+3=0的一个根是-1,则m的值是 -5 .
【解答】解:把x=-1代入2x2-mx+3=0,得2+m+3=0,
解得,m=-5.
故答案为:-5.
13.若关于x的分式方程=7有增根,则a的值为 3 .
【解答】解:原分式方程变形为 2-x+a=7(x-5),
∵分式方程有增根,
∴x-5=0,x=5为增根,
将x=5代入上式,
2-5+a=0,
∴a=3.
故答案为3.
14.如图,在周长为32的平行四边形ABCD中,AC、BD交于点O,OE⊥BD交AD于点E,则△ABE的周长为 16 .
【解答】解:
∵平行四边形ABCD的周长为32,
∴AB+AD=16,O为BD的中点,
∵OE⊥BD,
∴OE为线段BD的垂直平分线,
∴BE=DE,
∴AB+AE+BE=AB+AE+DE=AB+AD=16,
即△ABE的周长为16,
故答案为:16.
15.如图,在菱形ABCD中,∠B=45°,E、F分别是边CD,BC上的动点,连接AE、EF,G、H分别为AE、EF的中点,连接GH.若GH的最小值为3,则BC的长为 .
【解答】解:连接AF,
∵G,H分别为AE,EF的中点,
∴GH∥AF,且,
要使GH最小,只要AF最小,
当AF⊥BC时,AF最小,
∵GH的最小值为3,
∴AF=6,
∵∠B=45°,
∴∠BAF=45°,
∴BF=AF=6,
∴,
∵四边形ABCD是菱形,
∴.
故答案为:.
三.解答题
16.解方程:
(1)(x-1)2=3(x-1);
(2)x2-4x+1=0.
【解答】解:(1)∵(x-1)2=3(x-1),
∴(x-1)2-3(x-1)=0,
∴(x-1)(x-1-3)=0,
∴(x-1)(x-4)=0,
∴x-1=0或x-4=0,
x1=4,x2=1.
(2)∵x2-4x+1=0,
∴a=1,b=-4,c=1,
∴Δ=b2-4ac=(-4)2-4×1×1=12>0,
∴方程有两个不相等的实数根,
即,.
17.(1)解不等式组:并把它的解集在数轴上表示出来.
(2)先化简,再求值:,其中a=-2.
【解答】解:(1)解不等式①得,x≥-1,
解不等式②得,x>0,
所以不等式组的解集为x>0.
这个不等式组的解集在数轴上表示如图:
(2)解:
=•
=•
=•
=-2(a+3)
=-2a-6,
当a=-2时,原式=-2×(-2)-6=-2.
18.如图,方格纸中每个小正方形的边长都是1个单位长度,在方格纸中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上.
(1)将△ABC向右平移6个单位长度得到△A1B1C1,请画出△A1B1C1;
(2)画出△A1B1C1关于点O的中心对称图形△A2B2C2;
(3)若将△ABC绕某一点旋转可得到△A2B2C2,旋转中心的坐标为 (-3,0) .
【解答】解:(1)解:如图,△A1B1C1即为所求;
(2)如图,△A2B2C2即为所求;
(3)根据图形可知:
旋转中心的坐标为:(-3,0)
故答案为:(-3,0).
19.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB,交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形.
(2)若AB=5,BD=6,求OE的长.
【解答】(1)证明:∵AB∥CD,
∴∠CAB=∠DCA,
∵AC为∠DAB的平分线,
∴∠CAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD,
∵AB=AD,
∴AB=CD,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴平行四边形ABCD是菱形;
(2)解:∵四边形ABCD是菱形,对角线AC,BD交于点O,
∴AC⊥BD,OA=OC=,OB=OD=,
∴OB==3,
在Rt△AOB中,∠AOB=90°,
∴OA=,
∵CE⊥AB,
∴∠AEC=90°,
在Rt△AEC中,∠AEC=90°,O为AC中点,
∴=4.
20.某服装店老板用4000元购进了一批甲款T恤,用8800元购进了一批乙款T恤,已知所购乙款T恤数量是甲款T恤数量的2倍,购进的乙款T恤单价比甲款T恤单价贵5元.
(1)购进甲、乙两款T恤的单价分别是多少元?
(2)老板把这两种T恤的标价都定为每件100元,甲款T恤打九折销售,乙款T恤按标价销售.经过一段时间的销售,老板发现,销售两种T恤共100件时,利润不低于4200元.那么这段时间按标价销售的乙款T恤至少要销售多少件?
【解答】解:(1)设购进甲款T恤的单价是x元,则购进乙款T恤的单价是(x+5)元,
根据题意得:=×2,
解得:x=50,
经检验,x=50是所列方程的解,且符合题意,
∴x+5=50+5=55.
答:购进甲款T恤的单价是50元,乙款T恤的单价是55元;
(2)设这段时间按标价销售了y件乙款T恤,则销售了(100-y)件甲款T恤,
根据题意得:(100×0.9-50)(100-y)+(100-55)y≥4200,
解得:y≥40,
∴y的最小值为40.
答:这段时间按标价销售的乙款T恤至少要销售40件.
21.【问题情境】:如图1,点E为正方形ABCD内一点,AE=2,BE=4,∠AEB=90°,将直角三角形ABE绕点A逆时针方向旋转α度(0≤α≤180°)点B、E的对应点分别为点B′、E′.
【问题解决】:
(1)如图2,在旋转的过程中,点B′落在了AC上,求此时CB′的长;
(2)若α=90°,如图3,得到△ADE′(此时B′与D重合),延长BE交B′E′于点F,
①试判断四边形AEFE′的形状,并说明理由;
②连接CE,求CE的长;
(3)在直角三角形ABE绕点A逆时针方向旋转过程中,直接写出线段CE′长度的取值范围.
【解答】解:(1)∵AE=2,BE=4,∠AEB=90°,
∴AB===2,
∵四边形ABD是正方形,
∴BC=AB=2,∠ABC=90°,
∴AC=AB=2,
由旋转的性质得:AB'=AB=2,
∴CB′=AC-AB'=2-2;
(2)①四边形AEFE′是正方形,理由如下:
由旋转的性质得:AE'=AE,∠EAE'=α=90°,∠AE'D=∠AEB=90°,
∵∠AEF=180°-90°=90°,
∴四边形AEFE′是矩形,
又∵AE'=AE,
∴四边形AEFE′是正方形;
②过点C作CG⊥BE于点G,如图3所示:
则∠BGC=90°=∠AEB,
∴∠CBG+∠BCG=∠CBG+∠ABE=90°,
∴∠BCG=∠ABE,
在△BCG和△ABE中,
,
∴△BCG≌△ABE(AAS),
∴CG=BE=4,BG=AE=2,
∴EG=BE-BG=4-2=2,
∴CE===2;
(3)∵直角三角形ABE绕点A逆时针方向旋转α度(0≤α≤180°)点B、E的对应点分别为点B′、E′,
∴当α=0°时,E'与E重合,CE'最短=2;
当E‘落在CA的延长线上时,AE'=AE=2,CE'最长=AC+AE'=2+2,
∴线段CE′长度的取值范围是2≤CE'≤2+2.
22.问题提出
(1)如图①,在△ABC中,D、E分别是AB和AC的中点,连接DE,则DE与BC的数量关系是 DE=BC ,位置关系是 DE∥BC ;
问题探究
(2)如图②,在四边形ABCD中,∠BAC=90°,AB=AC=4,CD=4,E为AD中点,连接BE,求BE的最大值;
问题解决
(3)如图③,某小区计划在一片足够大的空地上修建四边形的花园ABCD,其中BC=20米,AD=CD,AD⊥CD,AB∥CD,由于受地理位置的影响,∠ABC<90°.根据要求,现计划给该花园修建条笔直的绿色长廊,且绿色长廊的入口O定为BC的中点,出口定为点D,为了尽可能地提高观赏体验,要求绿色长廊OD最长,试求绿色长廊OD最长为多少米?
【解答】解:(1)由题可知,D、E分别是AB和AC的中点,
∴DE为△ABC的中位线,∴DE∥BC且DE=BC;
故答案为:DE=BC,DE∥BC;
(2)如图,取AC的中点F,连接EF、BF,
∵E、F分别是AD和AC的中点,∴EF为△ADC的中位线,
∴EF∥DC且EF=CD=×4=2,
在Rt△ABF中,AB=4,AF=AC=2:BF==2;
在△BEF中,BF+EF>BE,
∴当B、E、F三点共线的时候BE最大,
即此时BE=BF+EF=2+2,
答:BE的最大值为2+2;
(3)过C作CM⊥AB于M点,在AD上截取DN使DN=BM,连接BN,取CN中点P,连接DP.OP,
∵CM⊥AB,AB∥CD,
∴∠CMA=∠MCD=∠ADC=90°,
∴四边形ADCM为矩形,
∵AD=CD.∴矩形ADCM为正方形,∴CD=CM,
在△CMB与△CDN中,,
∴△CMB≌△CDN(SAS),
∴CN=CB,∠BCM=∠NCD,
∴∠BCN=∠MCD=90°,
在Rt△BCN中,BC=CN=20,
∴BN==20,
在Rt△CDN中,点P为CN中点,∴DP=CN=10,
在Rt△BCN中,点P、O分别为CN、CB中点,
∴OP为△BCN的中位线,
∴OP∥BN且OP=BN=10,
在△OPD中,OP+PD>OD,∴当O、P.D三点共线的时OD最大,
即此时OD=OP+PD=10+10,
答:绿色长廊OD最长为(10+10)米.
47,广东省深圳市福田区红岭中学(红岭教育集团)2023-2024学年九年级下学期开学考试数学试题: 这是一份47,广东省深圳市福田区红岭中学(红岭教育集团)2023-2024学年九年级下学期开学考试数学试题,共24页。试卷主要包含了 2024的相反数是, 下列运算正确的是, 下列命题正确的是等内容,欢迎下载使用。
广东省深圳市福田区红岭中学(红岭教育集团)2023-2024学年七年级上学期期末数学试题: 这是一份广东省深圳市福田区红岭中学(红岭教育集团)2023-2024学年七年级上学期期末数学试题,共9页。试卷主要包含了下列说法正确的是等内容,欢迎下载使用。
广东省深圳市福田区红岭教育集团2023-2024学年九年级上学期期中数学试卷: 这是一份广东省深圳市福田区红岭教育集团2023-2024学年九年级上学期期中数学试卷,共23页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












