初中数学苏科版九年级上册2.4 圆周角优秀课时作业

第2章   对称图形----圆

2.4  圆周角

知识点01  圆周角的定义

1.圆周角定义：
像图中∠AEB、∠ADB、∠ACB这样的角，它们的顶点在圆上，并且两边都与圆相交的角叫做圆周角．

2.圆周角定理：
在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
3.圆周角定理的推论：
半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．
【微点拨】

(1)圆周角必须满足两个条件：①顶点在圆上；②角的两边都和圆相交.
(2)圆周角定理成立的前提条件是在同圆或等圆中.

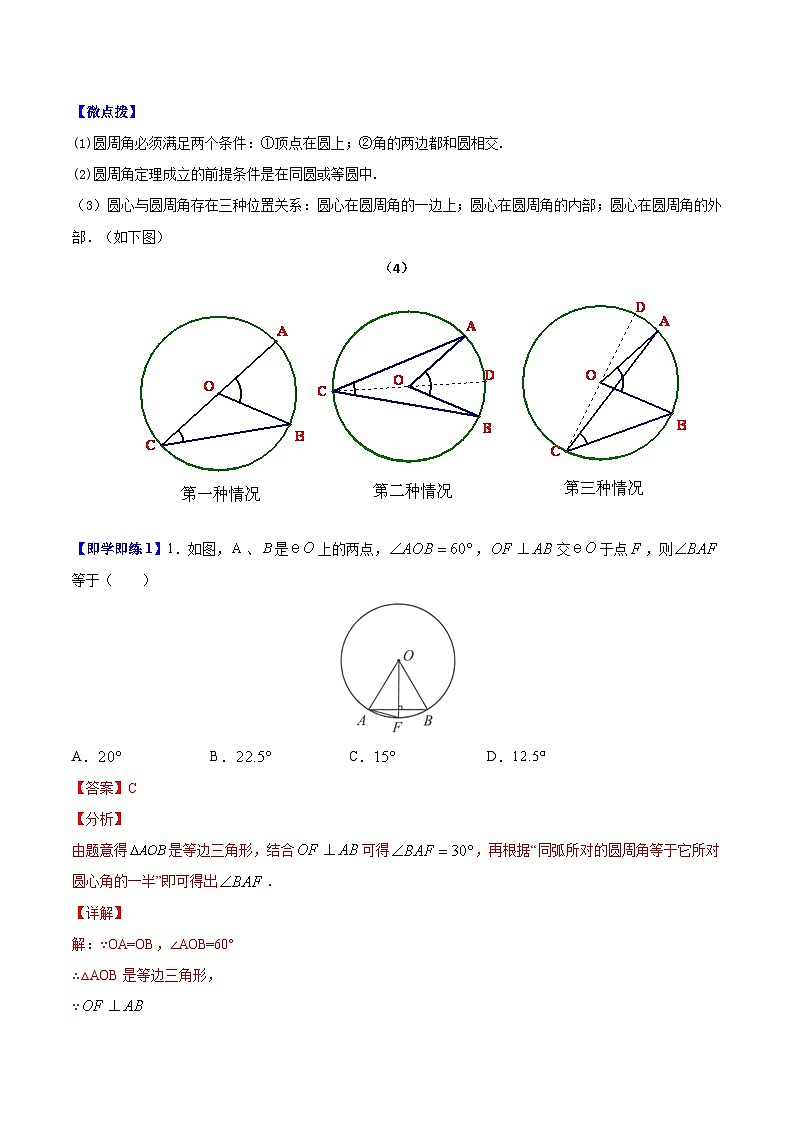
（3）圆心与圆周角存在三种位置关系：圆心在圆周角的一边上；圆心在圆周角的内部；圆心在圆周角的外部．（如下图）

（4）
    

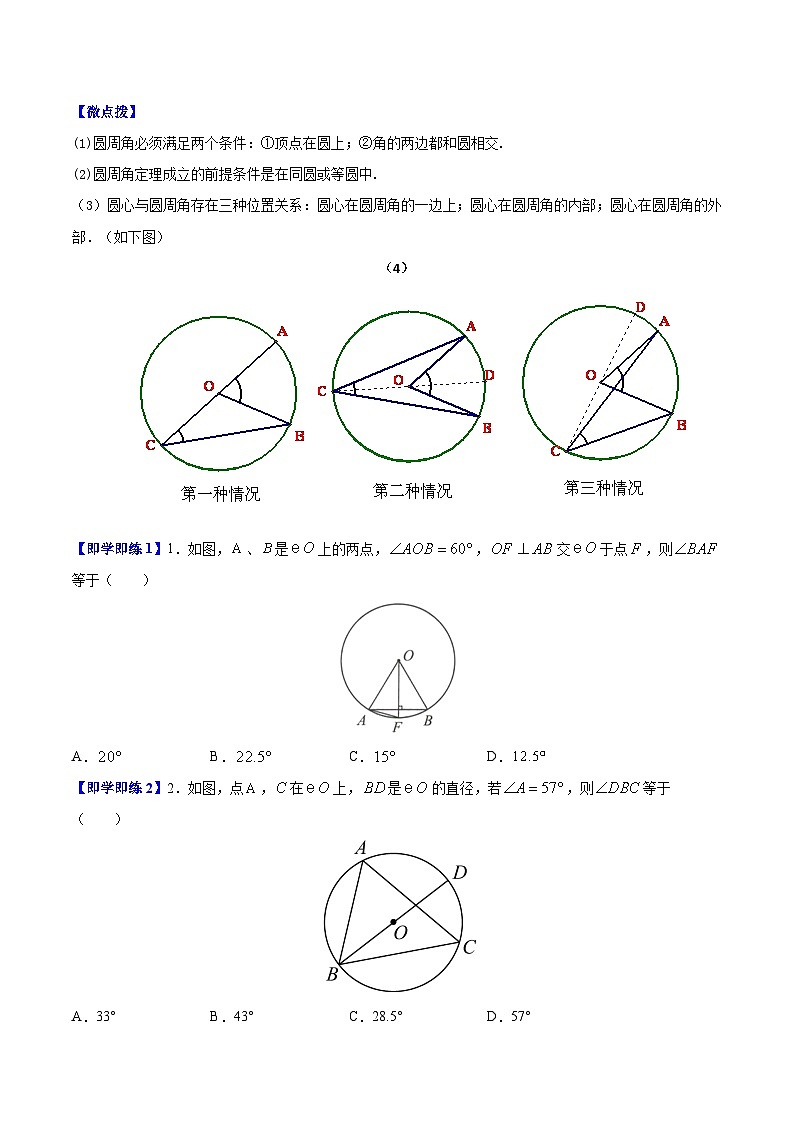
【即学即练1】1．如图，、是上的两点，，交于点，则等于（    ）

A． B． C． D．

【即学即练2】2．如图，点，在上，是的直径，若，则等于（    ）

A．33° B．43° C．28.5° D．57°

知识点02  圆内接四边形

如果一个四边形的各个顶点在同一个圆上，那么这个四边形叫做圆的内接四边形，这个圆叫做四边形的外接圆.

圆内接四边形的对角互补.

圆内接四边形的任意一个外角等于它的内对角（就是和它相邻的内角的对角）.

【微点拨】

圆内接四边形的性质是沟通角相等关系的重要依据，在应用此性质时，要注意与圆周角定理结合起来．在应用时要注意是对角，而不是邻角互补．

【即学即练3】3．如图，四边形是的内接四边形，是的直径，连接．若，则的度数是（    ）

A． B． C． D．

【即学即练4】4．如图，四边形内接于，、为其两条对角线，，，，连接，则的大小为（    ）

A． B． C． D．

考法01  圆周角定理

1、顶点在圆上,它们的两边在圆内的部分分别是圆的弦.

2、 圆周角定理：

一条弧所对的圆周角等于它所对的圆心角的一半。

3、 圆心角定理：

圆心角的度数等于它所对弧的度数。

推论1： 同弧或等弧所对的圆周角相等；同圆或等圆中，相等的圆周角所对的弧也相等。

推论2： 半圆（或直径）所对的圆周角是直角；90°的圆周角所对的弦是直径,高考物理。

3、圆周角的特点: (1)角的顶点在圆上; (2)角的两边在圆内的部分是圆的弦.

4、圆周角和圆心角相对于圆心与直径的位置关系有三种: 解题规律:

5、解决圆周角和圆心角的计算和证明问题,要准确找出同弧所对的圆周角和圆心角,然后再灵活运用圆周角定理

【典例1】如图，四边形ABCD内接于⊙O，E为DC延长线上一点．若∠BCE＝105°，则∠BOD的度数是（    ）

A．150° B．105° C．75° D．165°

考法02  已知圆内接四边形求角度

1、如果一个多边形的所有顶点都在同一个圆上，这个多边形叫做圆内接多边形，这个圆叫做这个多边形的外接圆．如图中的四边形ABCD叫做⊙O的内接四边形，而⊙O叫做四边形ABCD的外接圆．

2、边的性质：

（1）矩形：对边相等，对边平行．

（2）正方形：对边相等，对边平行，邻边相等．

（3）等腰梯形：两腰相等，有一组对边平行．

归纳：圆内接四边形的边之间看不出存在什么公同的性质．

3、角的关系

猜想：圆内接四边形的对角互补．

定理：圆的内接四边形的对角互补，并且任意一个外角等于它的内对角．

【典例2】如图，四边形ABCD内接于☉O，若∠A=80°，则∠C的度数是（    ）

A．80° B．100° C．110° D．120°

题组A  基础过关练

1．如图，在中，为直径，为弦，已知，则的度数为（ ）

A． B． C． D．

2．如图，点、、在⊙O上，，则的度数是（    ）

A． B． C． D．

3．如图，四边形内接于⊙O，若，则的度数为（    ）

A．18 B．72 C．100 D．108

4．如图，⊙O是△ABC的外接圆，∠A＝50°，则∠BOC的度数为（　　）

A．40° B．50° C．80° D．100°

5．如图，AB为⊙O的直径，C，D为⊙O上两点，若∠BDC＝30°，则∠ABC的大小为（    ）

A．30° B．60° C．70° D．80°

6．如图，AB为⊙O的直径，点C在⊙O上，∠A＝24°，则BC弧的度数为（　　）

A．66° B．48° C．33° D．24°

7．下列语句中正确的是（   ）

A．长度相等的两条弧是等弧 B．平分弦的直径垂直于弦

C．相等的圆心角所对的弧相等 D．直径所在直线是圆的对称轴

题组B  能力提升练

1．如图，中，，，．点为内一点，且满足．当的长度最小时，的面积是（   ）

A．3 B． C． D．

2．如图，内接于，其外角平分AD交于D，于M，则结论①②③④中正确的是（    ）

A．① B．①②③ C．③④ D．①②③④

3．如图，是的直径，点，点是半圆上两点，连结，相交于点，连结，．已知于点，．下列结论：①；②；③若，则；④若点为的中点，则．其中正确的是（    ）

A．①②③ B．②③④ C．③④ D．②④

4．如图，已知正方形的边长为2，点是正方形内部一点，连接，满足，点是边上一动点，连结，．则长度的最小值为（    ）

A． B． C． D．

5．在中，．点D为平面上一个动点，，则线段长度的最小值为_____．

6．如图在菱形中，，是、的交点，是线段上的动点（不与点、重合），将线段绕点顺时针旋转得到线段，点恰好在边上，若要使得，则的范围为________．

7．如图，在中，，，以为直径作半圆，交于点，则阴影部分的面积是___．

题组C  培优拔尖练

1．如图,点A是以BC为直径的半圆的中点，连接AB，点D是直径BC上一点，连接AD，分别过点B、点C向AD作垂线，垂足为E和F，其中，EF=2，CF=6，BE=8，则AB的长是（ ）

A．4 B．6 C．8 D．10

2．如图，在平面直角坐标系中,若在直线上存在点满足,则的取值范围是（  ）

A．

B．

C．

D．

3．如图，在中，直径垂直弦于点，且.点为上一点（点不与点，重合），连结，，，，.过点作于点.给出下列结论:①是等边三角形；②在点从的运动过程中，的值始终等于.则下列说法正确的是（  ）

A．①，②都对 B．①对，②错 C．①错，②对 D．①，②都错

4．已知锐角．如图（1）在射线上取一点，以点为圆心，长为半径作，交射线于点．连接；（2）分别以点、为圆心，长为半径作弧，交于点、；（3）连接，．根据以上作图过程及所作图形，下列结论中错误的是（）

A．

B．若，则

C．

D．点与点关于对称

5．如图，是半圆的直径，，点，在半圆上，，，点是上的一个动点，则的最小值为（    ）

A． B． C． D．

6．如图，、分别为的垂心、外心，，若外接圆的半径为2，则（    ）

A． B． C． D．

7．如图，已知正方形的边长为，点为正方形的中心，点为边上一动点，直线交于点，过点作，垂足为点，连接，则的最小值为（    ）

A．2 B． C． D．