人教版七年级上册4.3.1 角课后测评

这是一份人教版七年级上册4.3.1 角课后测评，文件包含七年级数学上册专题13与角相关的旋转翻折问题专项讲练原卷版docx、七年级数学上册专题13与角相关的旋转翻折问题专项讲练解析版docx等2份试卷配套教学资源，其中试卷共81页， 欢迎下载使用。

专题13 与角相关的旋转（翻折）问题 专项讲练
与角有关的旋转（翻折）问题属于人教版 七年级上期必考压轴题型，是尖子生必须要攻克的一块重要内容，对考生的综合素养要求较高。绝大部分学生对角度旋转问题信心不足，原因就是很多角度旋转问题需要自己画出图形，与分类讨论思想、数形结合思想等结合得很紧密，思考性强，难度大。本专题重点研究与角有关的旋转问题（求值问题；定值问题；探究问题；分类讨论问题）和与角有关的翻折问题。
【与角相关的旋转问题】
【解题技巧】
1、角度旋转问题解题步骤：
①找——根据题意找到目标角度；
②表——表示出目标角度：
1）角度一边动另一边不动，角度变大：目标角=起始角+速度×时间；
2）角度一边动另一边不动，角度变小：目标角=起始角—速度×时间；
3）角度一边动另一边不动，角度先变小后变大：
变小：目标角=起始角—速度×时间；变大：目标角=速度×时间—起始角
③列——根据题意列方程求解。
注：①注意题中是否确定旋转方向，未确定时要分顺时针与逆时针分类讨论；②注意旋转角度取值范围。
常见的三角板旋转的问题：三角板有两种，一种是等腰直角三角板(90°、45°、45°)，另一种是特殊角的直角三角板(90°、60°、30°)。三角板的旋转中隐藏的条件就是上面所说的这几个特殊角的角度。
总之不管这个角如何旋转，它的角度大小是不变的，旋转的度数就是组成角的两条射线旋转的度数（角平分线也旋转了同样的度数）。抓住这些等量关系是解题的关键，三角板只是把具体的度数隐藏了起来。
【重要题型】
题型1：求值问题
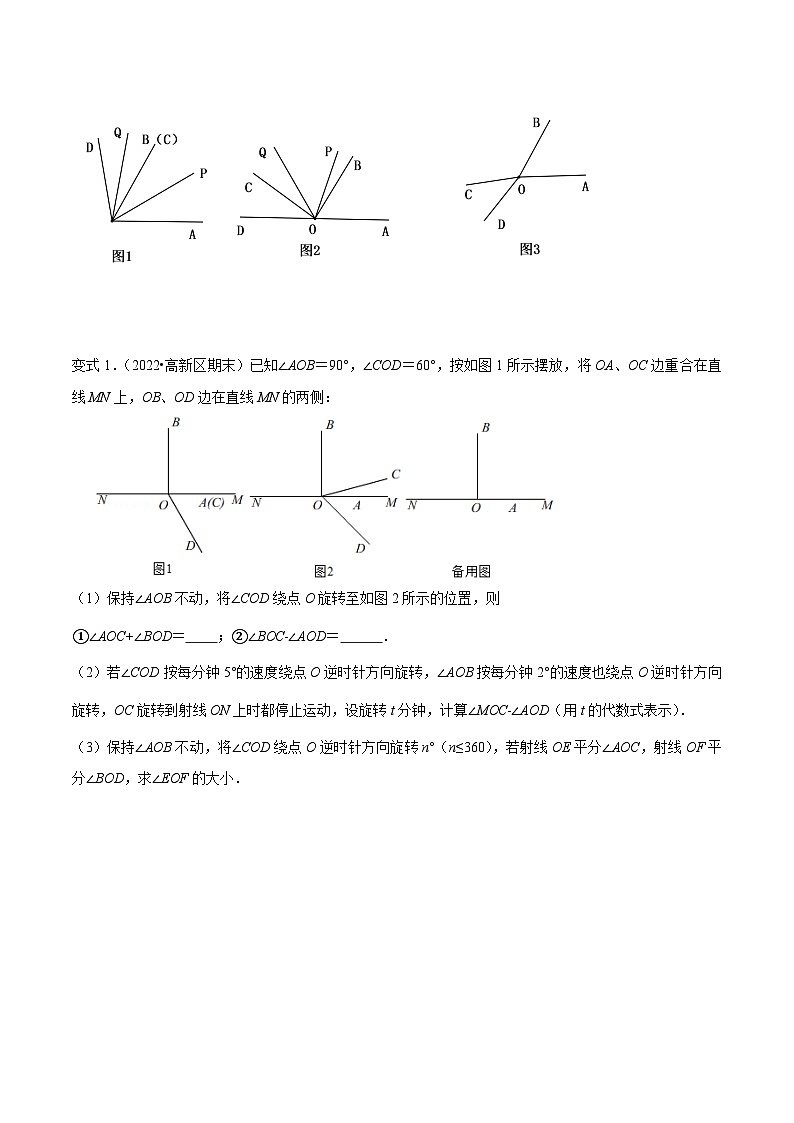
例1．（2022·江苏·七年级期中）已知∠AOB和∠COD均为锐角，∠AOB＞∠COD，OP平分∠AOC，OQ平分∠BOD，将∠COD绕着点O逆时针旋转，使∠BOC=α（0≤α＜180°）
（1）若∠AOB=60°，∠COD=40°，①当α=0°时，如图1，则∠POQ=　 　；②当α=80°时，如图2，求∠POQ的度数；③当α=130°时，如图3，请先补全图形，然后求出∠POQ的度数；
（2）若∠AOB=m°，∠COD=n°，m＞n，则∠POQ=　 　，（请用含m、n的代数式表示）．



变式1．（2022•高新区期末）已知∠AOB＝90°，∠COD＝60°，按如图1所示摆放，将OA、OC边重合在直线MN上，OB、OD边在直线MN的两侧：

（1）保持∠AOB不动，将∠COD绕点O旋转至如图2所示的位置，则
①∠AOC+∠BOD＝　 　；②∠BOC﹣∠AOD＝　 　．
（2）若∠COD按每分钟5°的速度绕点O逆时针方向旋转，∠AOB按每分钟2°的速度也绕点O逆时针方向旋转，OC旋转到射线ON上时都停止运动，设旋转t分钟，计算∠MOC﹣∠AOD（用t的代数式表示）．
（3）保持∠AOB不动，将∠COD绕点O逆时针方向旋转n°（n≤360），若射线OE平分∠AOC，射线OF平分∠BOD，求∠EOF的大小．








变式2.（2022•浙江七年级期中）如图1，为直线上一点，过点作射线，，将一直角三角板（）的直角顶点放在点处，一边在射线上，另一边与都在直线的上方．（注：本题旋转角度最多．）

（1）将图1中的三角板绕点以每秒的速度沿顺时针方向旋转．如图2，经过秒后，______度（用含的式子表示），若恰好平分，则______秒（直接写结果）．
（2）在（1）问的基础上，若三角板在转动的同时，射线也绕点以每秒的速度沿顺时针方向旋转，如图3，经过秒后，______度（用含的式子表示）若平分，求为多少秒？
（3）若（2）问的条件不变，那么经过秒平分？（直接写结果）




题型2：定值问题（角度不变问题）
例2．（2022·江苏南京·七年级期末）如图，两条直线AB，CD相交于点O，且∠AOC＝∠AOD，射线OM从OB开始绕O点逆时针方向旋转，速度为15°/s，射线ON同时从OD开始绕O点顺时针方向旋转，速度为12°/s，运动时间为t秒（0＜t＜12，本题出现的角均小于平角）

（1）图中一定有　 　个直角；当t＝2时，∠MON的度数为　 　，∠BON的度数为　 　；
（2）若OE平分∠COM，OF平分∠NOD，当∠EOF为直角时，请求出t的值；
（3）当射线OM在∠COB内部，且是定值时，求t的取值范围，并求出这个定值．





变式1．（2022•渝中区七年级期中）如图1，∠AOB＝40°，∠COD＝60°，OM、ON分别为∠AOB和∠BOD的角平分线．（1）若∠MON＝70°，则∠BOC＝　 　°；（2）如图2，∠COD从第（1）问中的位置出发，绕点O逆时针以每秒4°的速度旋转；当OC与OA重合时，∠COD立即反向绕点O顺时针以每秒6°的速度旋转，直到OC与OA互为反向延长线时停止运动．整个运动过程中，∠COD的大小不变，OC旋转后的对应射线记为OC′，OD旋转后的对应射线记为OD′，∠BOD′的角平分线记为ON′，∠AOD′的角平分线记为OP．设运动时间为t秒．①当OC′平分∠BON′时，求出对应的t的值；②请问在整个运动过程中，是否存在某个时间段使得|∠BOP﹣∠MON′|的值不变？若存在，请直接写出这个定值及其对应的t的取值范围（包含运动的起止时间）；若不存在，请说明理由．





变式2．（2022•碑林区七年级开学）如图1，点O为直线AB上一点，过点O作射线OC，使∠BOC＝120°，将一直角三角板的直角顶点放在点O处，一边OM在射线OB上，另一边ON在直线AB的下方．
（1）将图1中的三角板绕点O逆时针旋转至图2，使一边OM在∠BOC的内部，且恰好平分∠BOC，问：直线ON是否平分∠AOC？请直接写出结论：直线ON　平分　（平分或不平分）∠AOC．
（2）将图1中的三角板绕点O按每秒6°的速度沿逆时针方向旋转一周，在旋转的过程中，第t秒时，直线ON恰好平分锐角∠AOC，则t的值为　10或40　．（直接写出结果）
（3）将图1中的三角板绕点O顺时针旋转，请探究，当ON始终在∠AOC的内部时（如图3），∠AOM与∠NOC的差是否发生变化？若不变，请求出这个差值；若变化，请举例说明．




题型3：探究类问题（判断角的数量之间的关系）
例3．（2022·四川·成都市七年级期末）如图所示：点是直线上一点，∠是直角，平分∠．

（1）如图1，若∠=40°，求∠的度数；
（2）如图1，若∠=，直接写出∠的度数（用含的代数式表示）；
（3）保持题目条件不变，将图1中的∠按顺时针方向旋转至图2所示的位置，探究∠和∠的度数之间的关系，写出你的结论，并说明理由．

变式1．（2022·广东七年级期中）如图（a），将两块直角三角尺的直角顶点C叠放在一起．
（1）若∠DCE=25°，∠ACB 等于多少；若∠ACB=130°，则∠DCE 等于多少；
（2）猜想∠ACB与∠DCE的大小有何特殊关系，并说明理由；
（3）如图（b），若是两个同样的三角尺60°锐角的顶点A重合在一起，则∠DAB与∠CAE的大小有何关系，请说明理由；（4）已知∠AOB=α，∠COD=β（α、β都是锐角），如图（c），若把它们的顶点O重合在一起，则∠AOD与∠BOC的大小有何关系，请说明理由．




变式2．（2022•喀喇沁旗七年级期中）如图1，点O为直线AB上一点，过点O作射线OC，使∠BOC＝120°，将一直角三角板的直角顶点放在点O处，一边OM在射线OB上，另一边ON在直线AB的下方．
（1）将图1中的三角板绕点O逆时针旋转至图2，使点N在OC的反向延长线上，请直接写出图中∠MOB的度数；（2）将图1中的三角板绕点O顺时针旋转至图3，使一边OM在∠BOC的内部，且恰好平分∠BOC，求∠CON的度数；（3）将图1中的三角尺绕点O顺时针旋转至图4，使ON在∠AOC内部，请探究∠AOM与∠NOC之间的数量关系，并说明理由．




题型4：分类讨论问题
例4．（2022·成都市七中育才学校七年级月考）一副三角板（直角三角板和直角三角板）如图1所示放置，两个顶点重合于点，与重合，且，，，．将三角板绕着点逆时针旋转一周，旋转过程中，平分，平分，（和均是指小于180°的角）探究的度数．
（1）当三角板绕点旋转至如图2的位置时，与重合，______°，______°．
（2）三角板绕点旋转过程中，的度数还有其他可能吗？如果有，请研究证明结论，若没有，请说明理由．（3）类比拓展：当的度数为时，其他条件不变，在旋转过程中，请直接写出的度数．（用含的式子来表示）



变式1.（2022•广东七年级期末）如图（1），∠BOC和∠AOB都是锐角，射线OB在∠AOC内部，，．（本题所涉及的角都是小于180°的角）

(1)如图（2），OM平分∠BOC，ON平分∠AOC，填空：
①当，时，______，______，______；
②______（用含有或的代数式表示）．
(2)如图（3），P为∠AOB内任意一点，直线PQ过点O，点Q在∠AOB外部：
①当OM平分∠POB，ON平分∠POA，∠MON的度数为______；
②当OM平分∠QOB，ON平分∠QOA，∠MON的度数为______；
（∠MON的度数用含有或的代数式表示）
(3)如图（4），当，时，射线OP从OC处以5°/分的速度绕点O开始逆时针旋转一周，同时射线OQ从OB处以相同的速度绕点O逆时针也旋转一周，OM平分∠POQ，ON平分∠POA，那么多少分钟时，∠MON的度数是40°？





变式2．（2022·成都市七年级阶段练习）定义：从一个角的顶点出发，在角的内部引两条射线，如果这两条射线所成的角等于这个角的一半，那么这两条射线所成的角叫做这个角的内半角，如图1，若，则是的内半角．
（1）如图1，已知，，是的内半角，则________；
（2）如图2，已知，将绕点按顺时针方向旋转一个角度得，当旋转的角度为何值时，是的内半角；
（3）已知，把一块含有角的三角板如图3叠放，将三角板绕顶点以3度/秒的速度按顺时针方向旋转（如图4），问：在旋转一周的过程中，射线，，，能否构成内半角？若能，请求出旋转的时间；若不能，请说明理由．
    






【折叠（翻折）问题】
【解题技巧】
折叠前后对应角、对应边相等；出现角的比值或无角的具体度数却求度数常设列方程。在旋转问题中求解角度是初一数学的难点题型，需要熟悉并灵活运用角度求解的方法，本文就例题详细解析这类题型的解题思路，希望能给初一学生的数学学习带来帮助。
解决本题的关键是根据题目给出的角度或角与角之间的关系，确定射线旋转的角度，再根据射线的旋转速度，就可以求得射线旋转的时间，特别要注意在角的两边所处位置不明确的情况下，必须要考虑多解的可能。
例1．（2022·山东东营·期末）如图，长方形纸片，点、分别在边、上，连接．将对折，点落在直线上的点处，得折痕；将对折，点落在直线上的点处，得折痕．则的度数为（    ）

A． B． C． D．不能确定
变式1．（2022·辽宁沈阳·七年级期末）将一张长方形纸片按如图所示方式折叠，AE、AF为折痕，点B、D折叠后的对应点分别为、，若，则的度数为（    ）

A．40.5° B．41° C．41.5° D．42°
例2．（2022·辽宁西丰县·七年级期中）利用折纸可以作出角平分线．
（1）如图1，若∠AOB＝58°，则∠BOC＝　 　．
（2）折叠长方形纸片，OC，OD均是折痕，折叠后，点A落在点A′，点B落在点B'，连接OA'．
①如图2，当点B'在OA'上时，判断∠AOC与∠BOD的关系，并说明理由；
②如图3，当点B'在∠COA'的内部时，连接OB'，若∠AOC＝44°，∠BOD＝61°，求∠A'OB'的度数．





变式2．（2022·湖南长沙·七年级月考）已知长方形纸片ABCD， E、F分别是AD、AB上的一点，点I在射线BC上、连接EF，FI，将∠A沿EF所在的直线对折，点A落在点H处，∠B沿FI所在的直线对折，点B落在点G处．(1)如图1，当HF与GF重合时，则∠EFI＝_________°；
(2)如图2，当重叠角∠HFG＝30°时，求∠EFI的度数；
(3)如图3，当∠GFI＝α，∠EFH＝β时，∠GFI绕点F进行逆时针旋转，且∠GFI总有一条边在∠EFH内，PF是∠GFH的角平分线，QF是∠EFI的角平分线，旋转过程中求出∠PFQ的度数(用含α，β的式子表示)．





课后专项训练
1．（2022·偃师市实验中学初一月考）如图,将长方形纸片ABCD的∠C沿着GF折叠(点F在BC上,不与B,C重合),使点C落在长方形内部的点E处,若FH平分∠BFE,则∠GFH的度数是____. 

2．（2022·东平县实验中学初一期中）将一张长方形纸片按如图所示的方式折叠，BD、BE为折痕，若∠CBD＝66°，则∠ABE＝_________.

3．（2022·重庆七年级期中）如图，将一张长方形纸片ABCD沿对角线BD折叠后，点C落在点E处，连接BE交AD于F，再将三角形DEF沿DF折叠后，点E落在点G处，若DG刚好平分∠ADB，那么∠ADB的度数是（　　）

A．18° B．20° C．36° D．45°
4．（2022·山西·初一期末）如图1，长方形纸片，点分别在边上，连接，将对折，点落在直线上的点处，的到折痕；将对折，点落在直线上的点处，得到折痕.（1）求的度数. （2）如图2，在（1）的基础上，将纸片展平，然后将对折，点落在直线上的处，得到折痕，猜想和的数量关系，并说明理由.
图1 图2







4．（2022·四川省金堂实验中学初一月考）如图，以直线 AB 上一点 O 为端点作射线 OC，使∠BOC=70°，将一个直角三角形的直角顶点放在点 O 处．（注：∠DOE=90°）
(1)如图①，若直角三角板 DOE 的一边 OD 放在射线 OB 上，则∠COE= °；
(2)如图②，将直角三角板 DOE 绕点 O 逆时针方向转动到某个位置，若 OC 恰好平分∠BOE，求∠COD 的度数；(3)如图③，将直角三角板 DOE 绕点 O 转动，如果 OD 始终在∠BOC 的内部， 试猜想∠BOD 和∠COE 有怎样的数量关系？并说明理由．







5．（2022·山东·济南市天桥区泺口实验学校七年级期中）将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起，其中∠A=60°，∠B=45°．

(1)如图1，若∠DCE=40°，则∠ACE= ．∠ACB= ．
(2)由（1）猜想∠ACB和∠DCE的数量关系，并证明你的结论：
(3)若固定△ACD，将△BCE绕点C旋转．①如图2，当旋转至BEAC时，则∠ACE= ．
②如图3，当旋转至BCAD时，则∠ACE= ．



6．（2022·上海·七年级专题练习）（1）已知：如图1，P是直角三角板ABC斜边AB上的一个动点，CD、CE分别是∠ACP和∠BCP的平分线．当点P在斜边AB上移动时，∠DCE＝　 　°；
（2）把直角三角板的直角顶点C放在直尺的一边MN上：
①点A和点B在直线MN的上方（如图2），此时∠ACM与∠BCN的数量关系是∠ACM+∠BCN＝　 　；
②当把这把直角三角板绕顶点C旋转到点A在直线MN的下方、点B仍然在直线MN的上方时（如图3），∠ACM与∠BCN的数量关系是　 　；
③当把这把直角三角板绕顶点C旋转到点A和点B都在直线MN的下方时（如图4），∠ACM与∠BCN的数量关系是　 　．


7．（2022·湖南株洲·七年级期末）点为直线上一点，过点作射线，使，将一直角三角板的直角顶点放在点处．

(1)如图1，当三角板的一边与射线重合时，则________；
(2)如图2，将三角板绕点逆时针旋转一定角度，此时是的平分线，求和的度数；(3)将三角板绕点逆时针旋转至图3所示的位置时，，求的度数．




8．（2022·江苏盐城·七年级期末）【阅读理解】
如图1，一套三角板如图拼在一起，我们将三角板COD绕点O以每秒15°的速度顺时针旋转180°．

【解决问题】（1）在旋转过程中，∠AOB、∠AOC、∠BOC之间有怎样的数量关系？
（2）当运动时间为9秒时，图中有角平分线吗？找出并说明理由．
（3）运动过程中，如图2，形成的三个角：∠AOB、∠AOC、∠BOC，当其中一个角的度数是另一个角的两倍时，则称射线OC是∠AOB的“优线”．①第（2）问中旋转后的射线OC是“优线”吗？为什么？
②在整个旋转过程中，若旋转时间记为t秒，当射线OC是“优线”时，请直接写出所有满足条件的t值．
9．（2022·江苏连云港·七年级期末）【问题提出】
七年级上册《数学实验手册》中有“三角尺拼角”的问题．
(1)①填空：如图（1），用副三角板可以直接画出大于小于的角，它们是：
，，，，，，，，______，，．
②如果用两副三角板能画出吗？________．（填“能”或“不能”）

(2)【问题探究】如图（2），现有、角的两种模板，，，请设计一种方案，只用给出的模板和铅笔画出角．
小明想出了一个方案，利用角模板画出角．动手操作：如图（3），M、O、N三点在一条直线上，的顶点A与点O重合，边与射线重合，如图所示，将绕点O逆时针旋转，得，再将绕点O逆时针旋转，得，…，如此连续操作52次．再利用两个平角等于一个周角，可得的角，即：．
请聪明的你设计一个方案，利用角模板画出角，并说明理由．

(3)【问题拓展】现将【问题探究】中两种模板按照如图（4）所示放置，即M、O、N三点在一条直线上，与的顶点A、D都与点O重合，、边与射线重合．动手操作：将绕点O以每秒的速度逆时针方向旋转一周，同时也绕点O以每秒的速度逆时针方向旋转一周，当一方先完成旋转一周时，另一方随之停止转动．．设运动时间为t（秒）．

①当t为何值时，？
②请直接写出在旋转过程中，与的数量关系（数量关系中不能含t）．




10．（2022·安徽亳州·七年级期末）如图（）所示，将两块直角三角尺的直角顶点C叠放在一起．

(1)若，则________°；若∠ACB=130°，则_________°．
(2)如图（b）所示，若两个同样的三角板，将锐角的顶点A叠放在一起，则与有何数量关系，请说明理由．
(3)如图（c）所示，已知，（，都是锐角）．若把它们的顶点O叠放在一起，则与有何数量关系，直接写出结论．





11．（2022·福建泉州·七年级期末）如图，，射线以的速度从位置出发，射线以的速度从位置出发，设两条射线同时绕点逆时针旋转．
(1)当时，求的度数；(2)若．①当三条射线、、构成的三个度数大于的角中，有两个角相等，求此时的值；②在射线，转动过程中，射线始终在内部，且平分，当，求的值．




12．（2022·安徽·定远县第一初级中学七年级期末）已知，，OM，ON分别是和的平分线．(1)如图1，如果OA，OC重合，且OD在的内部，求的度数；
(2)如图2，固定，将图1中的绕点O顺时针旋转（）．①与旋转度数有怎样的数量关系？说明理由；②当n为多少时，为直角？(3)如果的位置和大小不变，的边OD的位置不变，改变的大小；将图1中的OC绕着O点顺时针旋转（），如图3，请直接写出与旋转度数之间的数量关系：_____．




13．（2022·湖北武汉·七年级期末）【学习概念】 如图1，在∠AOB的内部引一条射线OC，则图中共有3个角，分别是∠AOB、∠AOC和∠BOC．若其中有一个角的度数是另一个角度数的两倍，则称射线OC是∠AOB的“好好线”．
【理解运用】（1）①如图2，若∠MPQ＝∠NPQ，则射线PQ ∠MPN的“好好线”（填“是”或“不是”）；
②若∠MPQ≠∠NPQ，∠MPQ＝α，且射线PQ是∠MPN的“好好线”，请用含α的代数式表示∠MPN；
【拓展提升】 （2）如图3，若∠MPN＝120°，射线PQ绕点P从PN位置开始，以每秒12°的速度逆时针旋转，旋转的时间为t秒．当PQ与PN成110°时停止旋转．同时射线PM绕点P以每秒6°的速度顺时针旋转，并与PQ同时停止． 当PQ、PM其中一条射线是另一条射线与射线PN的夹角的“好好线”时，则t＝ 秒．



14．（2022·江苏淮安·七年级期末）
【阅读理解】射线OC是∠AOB内部的一条射线，若∠AOC＝∠BOC，则称射线OC是射线OA在∠AOB内的一条“友好线”．如图1，若∠AOB＝75°，∠AOC＝25°，则∠AOC＝∠BOC，所以射线OC是射线OA在∠AOB内的一条“友好线”．
【解决问题】(1)在图1中，若作∠BOC的平分线OD，则射线OD　 　（填“是”或“不是”）射线OB在∠AOB内的一条“友好线”；
(2)如图2，∠AOB的度数为n，射线OM是射线OB在∠AOB内的一条“友好线”，ON平分∠AOB，则∠MON的度数为 　 　（用含n的代数式表示）；
(3)如图3，射线OB先从与射线OA重合的位置出发，绕点O以每秒1°的速度逆时针旋转；10秒后射线OC也从与射线OA重合的位置出发，绕点O以每秒5°的速度逆时针旋转，当射线OC与射线OA的延长线重合时，运动停止．问：当射线OC运动时间为多少秒时，射线OA，OB，OC中恰好有一条射线是余下两条射线中某条射线在余下两条射线所组成的角内的一条“友好线”？



15．（2022·江苏无锡·七年级期末）类比角平分线的概念，如果一条射线把一个角分成1：2两部分，则称这条射线为这个角的一条三等分线，
(1)如图，已知，是的一条三等分线，．且，求的度数；

(2)如图，，是的一条三等分线（），是的角平分线，是的角平分线．若以每秒5的速度绕点O逆时针旋转一周，旋转时间为t秒，当t为何值时，射线恰好是的一条三等分线．




16．（2022·扬州市七年级期末）如图1，点O为直线AB上一点，过O点作射线OC，使∠BOC=120°．将一块直角三角板的直角顶点放在点O处，边OM与射线OB重合，另一边ON位于直线AB的下方．（1）将图1的三角板绕点O逆时针旋转至图2，使边OM在∠BOC的内部，且恰好平分∠BOC，问：此时ON所在直线是否平分∠AOC？请说明理由；
（2）将图1中的三角板绕点O以每秒6°的速度沿逆时针方向旋转一周，设旋转时间为t秒，在旋转的过程中，ON所在直线或OM所在直线何时会恰好平分∠AOC？请求所有满足条件的t值；
（3）将图1中的三角板绕点O顺时针旋转至图3，使边ON在∠AOC的内部，试探索在旋转过程中，∠AOM和∠CON的差是否会发生变化？若不变，请求出这个定值；若变化，请求出变化范围．



17．（2022·宿迁市初一期末）如图，以直线 AB 上一点 O 为端点作射线 OC，使∠BOC=70°，将一个直角三角形的直角顶点放在点 O 处．（注：∠DOE=90°）
(1)如图①，若直角三角板 DOE 的一边 OD 放在射线 OB 上，则∠COE= °；
(2)如图②，将直角三角板 DOE 绕点 O 逆时针方向转动到某个位置，若 OC 恰好平分∠BOE，求∠COD 的度数；(3)如图③，将直角三角板 DOE 绕点 O 转动，如果 OD 始终在∠BOC 的内部， 试猜想∠BOD 和∠COE 有怎样的数量关系？并说明理由．