中职数学高教版（2021）基础模块上册4.2 弧度制教案

授课题目

4.2  弧度制

选用教材

高等教育出版社《数学》

（基础模块上册）

授课

时长

2 课时

授课

类型

新授课

教学提示

本课通过类比其他度量制，感知弧度制引入的可能性和必要性，学习引入弧度制的意义，进行角度与弧度的换算的一般方法，学习弧度制

下弧长公式和扇形面积公式的推导，并会进行有关的计算.

教学目标

能从熟悉的角度制引申到弧度制，知道引入弧度的必要性，理解定义 1 弧度的合理性，知道使用弧度制的优势，逐步提升数学抽象等核心素养；能区分角度制与弧度制，知道角度与弧度的换算关系，能将角度与弧度进行互化，会用函数型计算器进行给定角度与弧度的互化，逐步提升数学运算等核心素养；经历弧度制下弧长公式和扇形面积公式的推出过程，并能应用公式求弧长和扇形的面积，提升学生思考问题的意识

与解决问题的能力，逐步提升数学运算和直观想象等核心素养．

教学

重点

角度与弧度的转化.

教学

难点

1 弧度角的定义的理解.

教学

环节

教学内容

教师

活动

学生

活动

设计

意图

引入

    日常生活中，有些量可以用不同的单位进行度量．如，度量温度可以用℃(摄氏温度)、F(华氏温度)、K(热力学温度)等不同单位．

在义务教育阶段, 用角度制来度量角．即把一个周角 360 等分, 每一份圆弧所对的圆心角就是 1°的角．用角度制度量角用的是六十进制,  而日常的运算多数是十进制,  能否建立一

种十进制的度量体系来度量角呢？

讲解介绍提问

回忆思考作答

借助原有知识为学习做好铺垫

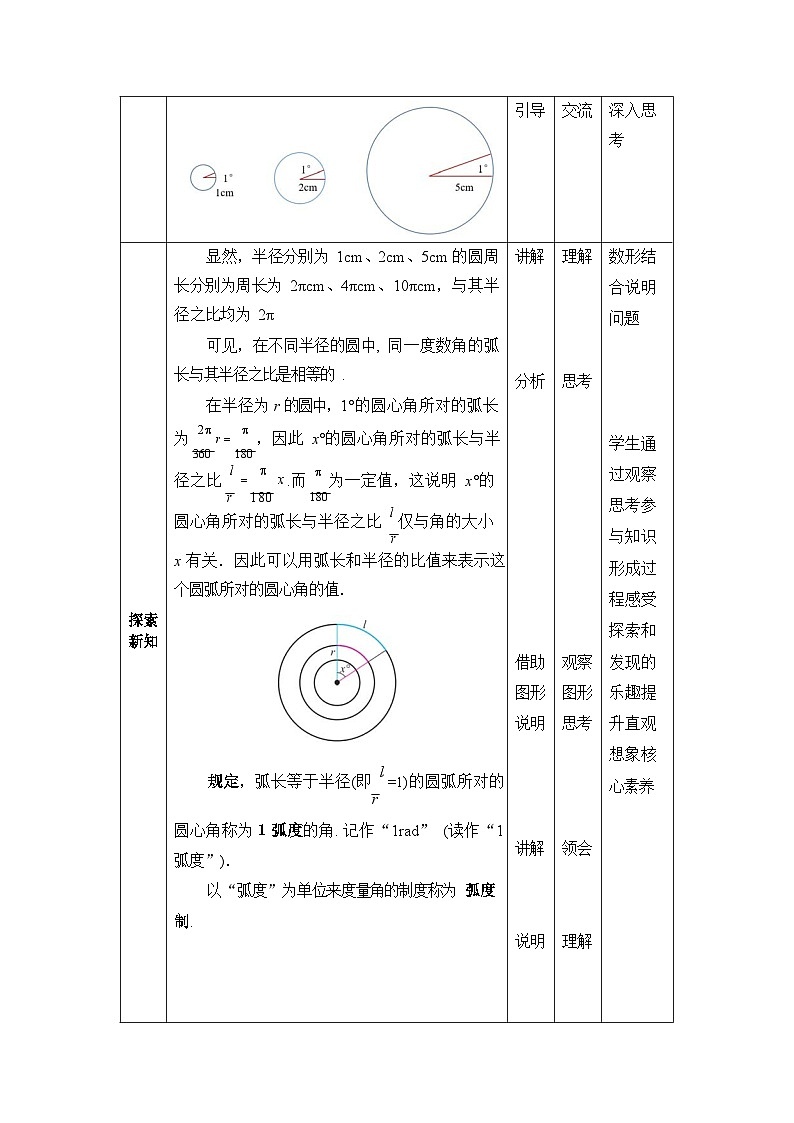
情境导入

在半径分别为 1cm、2cm、5cm 的圆中, 圆周角所对的弧长与半径之比分别为多少？

提问启发

思考作答

增强感性认识同时引

发学生

引导

交流

深入思考

显然，半径分别为 1cm、2cm、5cm 的圆周长分别为周长为 2πcm、4πcm、10πcm，与其半径之比均为 2π

可见，在不同半径的圆中, 同一度数角的弧长与其半径之比是相等的.

在半径为 r 的圆中，1°的圆心角所对的弧长

为 2 r      ，因此 x°的圆心角所对的弧长与半

360 180

径之比 l        x .而   为一定值，这说明 x°的

r 180 180

圆心角所对的弧长与半径之比 l 仅与角的大小

r

x 有关．因此可以用弧长和半径的比值来表示这个圆弧所对的圆心角的值．

规定，弧长等于半径(即 l =1)的圆弧所对的

r

圆心角称为１弧度的角. 记作“1rad” (读作“1

弧度”)．

以“弧度”为单位来度量角的制度称为弧度

制.

讲解

理解

数形结

合说明

问题

分析

思考

学生通

过观察

思考参

与知识

形成过

程感受

探索

新知

探索和

借助

观察

发现的

图形

图形

乐趣提

说明

思考

升直观

想象核

心素养

讲解

领会

说明

理解

同时规定，正角的弧度数是正数，负角的弧度数是负数，零角的弧度数是零.

半径为 r 的圆中, 长度为 l 的圆弧所对的圆心角的大小为 α, 那么

| |  l .

r

其中，角 α 的正负由角 α 的终边的旋转方向决定.

因为半径为 r 的圆的周长是 2πr，所以周角的弧度数是

2r =2，

r

故有

360°=2π rad

或

180°=π rad.

由此可得弧度制与角度制的换算公式：

数形结

讲解

思考

合解决

问题同

时提升

数学运

算和直

观想象

借助

观察

核心素

图形

图形

养

说明

理解

补充说

引导

理解

明

讲解

思考

举例

交流

总结

结论

理解

记忆

温馨提示

用弧度制表示角时,可以省略单位“rad”．如 “2rad”可以写成“2”．

但是，在用角度制表示角时,不能省略单位

“°”.

讲解说明

理解体会

例1 把−100°转换为弧度.

解 100 = 100       rad=  5 rad .

180 9

例 2 把 8 化成角度．

5



解 8  8   180    288 .

5 5     

 

例 3 扇形的圆心角为 α(0＜α＜2π) ，半径为 r，弧长为 l，扇形面积为 S，求证：(1) l=αr ;              (2)

S = 1 lr.

2

证明 (1)因为| | l ，而 0＜α＜2π，所以  l ，

r r

即 l=αr.

(2) 因为 圆心角 为 1rad   的扇形面积为

1 2   r 2

 r    ，所以圆心角为的扇形面积为

22

r 2      l  r 2 1

S       lr.

2 r   2 2

例 4 利用函数型计算器进行角度与弧度的换算：

(1)把67°30′化成弧度（精确到0.01）；

(2)把3.14rad化成角度（精确到0.01°）．

提问

思考

巩固角

引导

分析

度与弧

度转换

讲解

解决

常用方

强调

交流

法

以证明

题方式

提问

思考

给出弧

度制下

弧长和

引导

分析

扇形面

例题

积公式

辨析

讲解

解决

强调

交流

介绍借

助信息

技术多

种计算

方式提

升学生

展示

操作

运用计

分析 利用科学型计算器进行角度与弧度的转换时，应先确定角的度量单位．设置角的度量单位为“度”或“弧度”的方法是：依次按键： SHIFT→MODE SETUP→3(角度制模式)或

4(弧度制模式).

解 (1)第一步：将科学型计算器设为弧度制模式：

SHIFT→MODE SETUP→4

第二步：输入 67°30′，并把它转换为弧度 ： 6→7→.,,,,→3→0→.,,,,→SHIFT→Ans→1→=

→S¾D，

结果显示 1.178097245．

因此， 67°30′≈1.18rad．

(2)第一步：将科学型计算器设为角度制模式：

SHIFT→MODE SETUP→3

第二步：输入 3.14rad，并把它转换为角度：

3→.→1→4→SHIFT→Ans→2→=， 结果显示 179.9087477．

因此， 3.14 rad≈179.91°．温馨提示

算工具

解决问

分析

思考

题的能

讲解

领会

力

适时总

结加深

指导

尝试

印象

讲解

领会

演示

操作

提示

完成

总结

表格

练习 4.2

1. 把下列角度转换为弧度．

(1)22°； (2) −210°； (3) 1200°．

2. 把下弧度转换为角度．

(1)  ； (2)  4 ； (3)3．

12 3

3.经过4小时，时钟的时针和分针各转了多少度，将其化成弧度？

4.用弧度制表示终边在x轴上的角的集合．

5.已知一个扇形的半径为 10 cm，圆心角为

1.2rad，求该扇形的弧长和面积．

提问

思考

通过练

习及时

掌握学

巩固

生的知

练习

巡视

动手

识掌握

求解

情况，查

漏补缺

指导

交流

引导

回忆

培养学

生总结

归纳总结

提问

反思

学习过程能力

1.书面作业：完成课后习题和学习与训练；

说明

记录

继续探

布置

2.查漏补缺：根据个人情况对课题学习复习与回

究

作业

顾;

延伸学

3.拓展作业：阅读教材扩展延伸内容.

习