基础模块上册4.5 诱导公式教学ppt课件

这是一份基础模块上册4.5 诱导公式教学ppt课件，共25页。

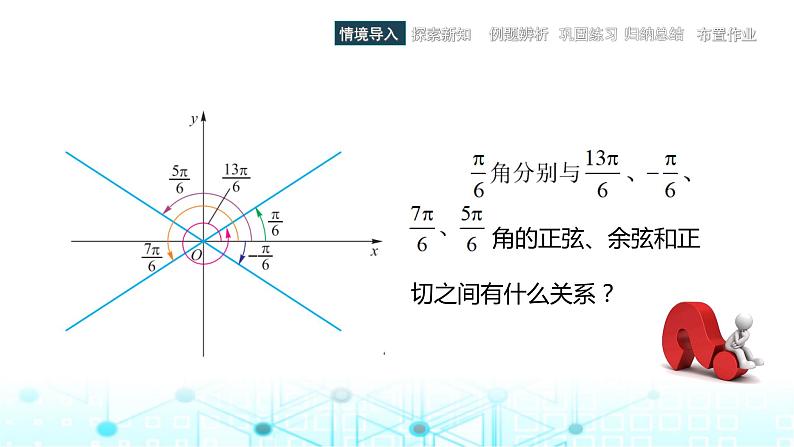
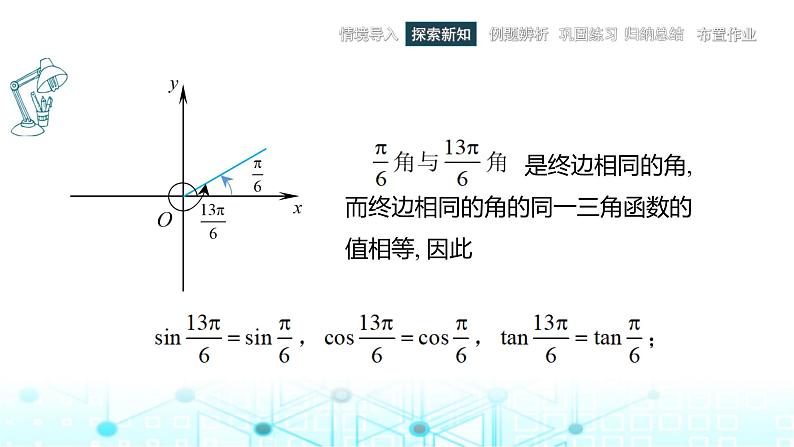
1.角2k＋ (kZ)与角 的三角函数值之间的关系
由三角函数的定义可知，终边相同的角的同一三角函数值相等．即
sin(2k＋)= sin；cs(2k＋)= cs；tan(2k＋)= tan.
由公式可以将任意角的三角函数值转化为[0,2π）内的角的三角函数值．
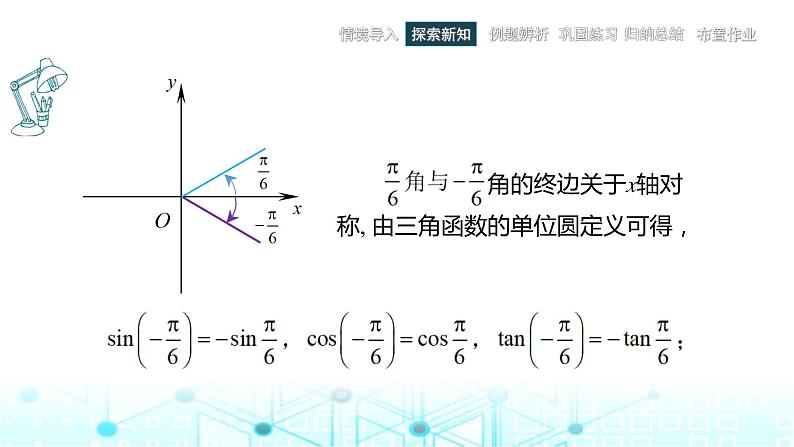
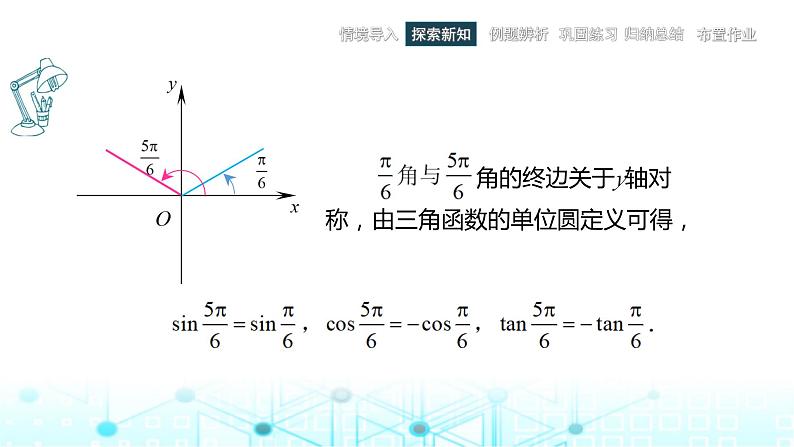
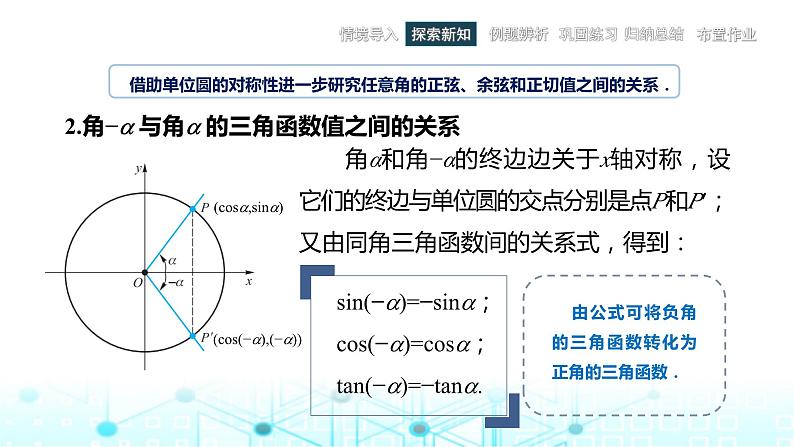
2.角− 与角 的三角函数值之间的关系
角α和角−α的终边边关于x轴对称，设它们的终边与单位圆的交点分别是点P和P；又由同角三角函数间的关系式，得到：
sin(−)=−sin；cs(−)=cs；tan(−)=−tan.
由公式可将负角的三角函数转化为正角的三角函数．
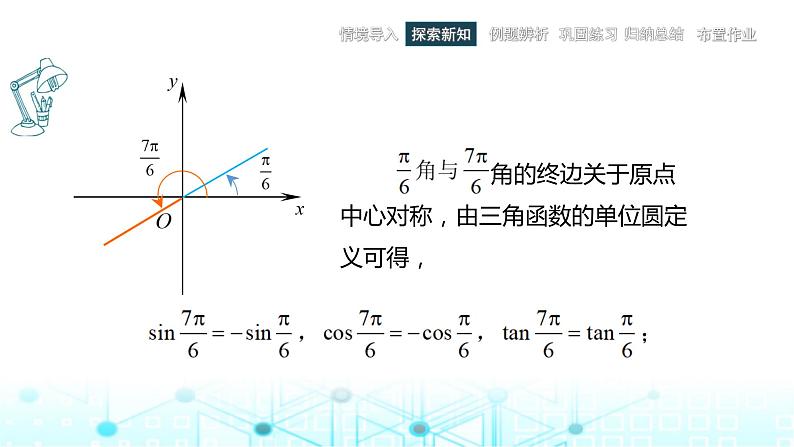
3.角＋α与角α的三角函数值之间的关系
角α的终边与角＋α的终边关于原点O中心对称，设它们的终边与单位圆的交点分别为点P和P；又由同角三角函数间的关系式，得到：
sin(π+)=−sin；cs(π+)=−cs；tan(π+)=tan.
由公式可将角＋α的三角函数值转化为角α的三角函数值．
4.角−α与角α的三角函数值之间的关系
sin(−α)=sin[π+(−α)]=−sin(−α)=−(−sinα)=sinα； cs(−α)=cs[π+(−α)]=−cs(−α)=−csα； tan(−α)=tan[π+(−α)]=tan+(−α)=−tanα．即
sin(−α) )=sinα ；cs(−α)=−csα；tan(−α)=−tanα.
由公式可将角−α的三角函数值转化为角α的三角函数值．
这些都三角函数的诱导公式，利用这些公式可以将任意角的三角函数转化为锐角三角函数进行计算.
例3 求下列三角函数值.
把任意角的三角函数转化为锐角三角函数的一般步骤是什么？ 可以结合-750°、 225° 、 510° 举例说明.
在实际问题中，经常利用科学型计算器求任意角的三角函数值． 用科学型计算器计算任意角的三角函数值的主要步骤是： 设置模式(角度制或弧度制)→按键sin(或按键cs、tan)→输入角的大小→按键=显示结果．
例6 利用科学型计算器，求下列各三角函数值(保留到小数点后第三位).
1.利用诱导公式求下列各三角函数值：
2.将下列函数转化为 内的角的三角函数值：