高教版（2021·十四五）基础模块 下册5.3 对数教案

这是一份高教版（2021·十四五）基础模块 下册5.3 对数教案，共4页。
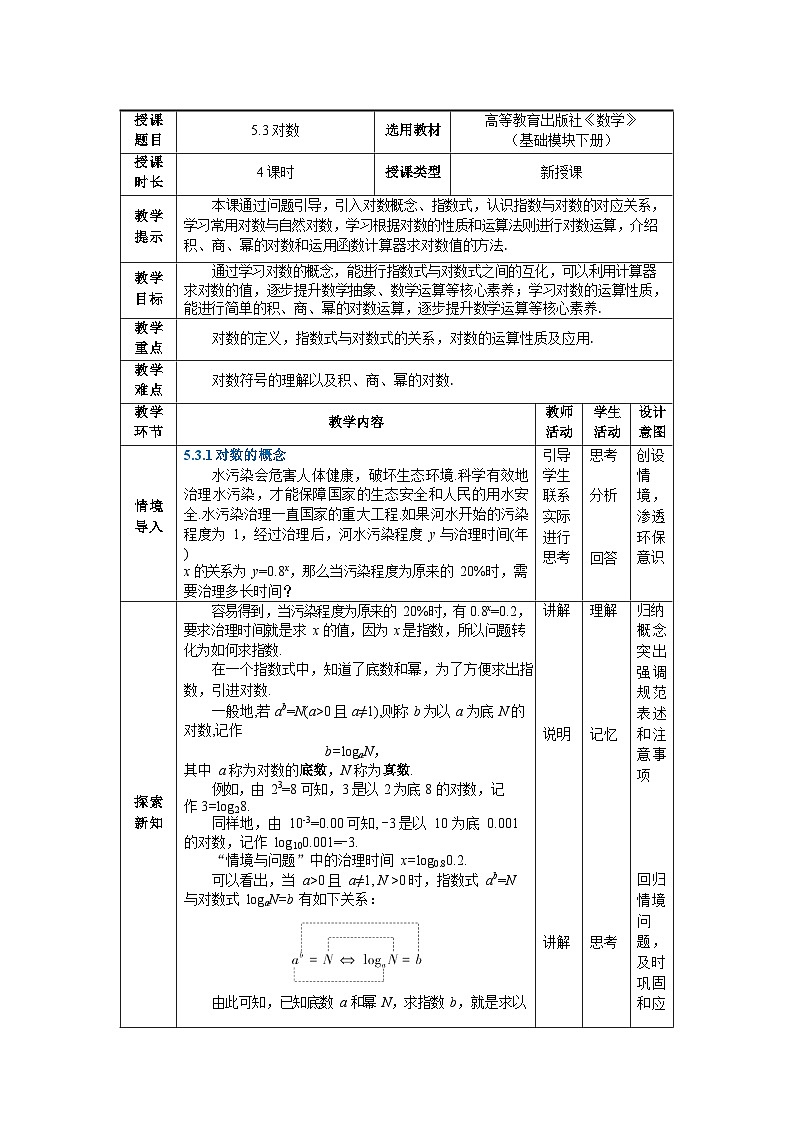
授课题目5.3 对数选用教材高等教育出版社《数学》（基础模块下册）授课时长4 课时授课类型新授课教学提示本课通过问题引导，引入对数概念、指数式，认识指数与对数的对应关系，学习常用对数与自然对数，学习根据对数的性质和运算法则进行对数运算，介绍积、商、幂的对数和运用函数计算器求对数值的方法.  教学目标通过学习对数的概念，能进行指数式与对数式之间的互化，可以利用计算器求对数的值，逐步提升数学抽象、数学运算等核心素养；学习对数的运算性质， 能进行简单的积、商、幂的对数运算，逐步提升数学运算等核心素养.教学重点对数的定义，指数式与对数式的关系，对数的运算性质及应用.教学难点对数符号的理解以及积、商、幂的对数.教学环节教学内容教师活动学生活动设计意图   情境导入5.3.1 对数的概念水污染会危害人体健康，破坏生态环境.科学有效地治理水污染，才能保障国家的生态安全和人民的用水安全.水污染治理一直国家的重大工程.如果河水开始的污染程度为 1，经过治理后，河水污染程度 y 与治理时间(年)x 的关系为 y=0.8x，那么当污染程度为原来的 20%时，需要治理多长时间？引导学生联系实际进行思考思考 分析   回答创设情 境， 渗透环保意识            探索新知容易得到，当污染程度为原来的 20%时，有 0.8x=0.2，要求治理时间就是求 x 的值，因为 x 是指数，所以问题转化为如何求指数.在一个指数式中，知道了底数和幂，为了方便求出指数，引进对数.一般地,若 ab=N(a>0 且 a≠1),则称 b 为以 a 为底 N 的对数,记作b=logaN，其中 a 称为对数的底数，N 称为真数.例如，由 23=8 可知，3 是以 2 为底 8 的对数，记作 3=log28.同样地，由 10-3=0.00 可知, -3 是以 10 为底 0.001的对数，记作 log100.001=-3.“情境与问题”中的治理时间 x=log0.80.2.可以看出，当 a>0 且 a≠1, N >0 时，指数式 ab=N与对数式 logaN=b 有如下关系： 由此可知，已知底数 a 和幂 N，求指数 b，就是求以讲解       说明            讲解理解       记忆            思考归纳概念突出强调规范表述和注意事项     回归情境问 题， 及时巩固和应
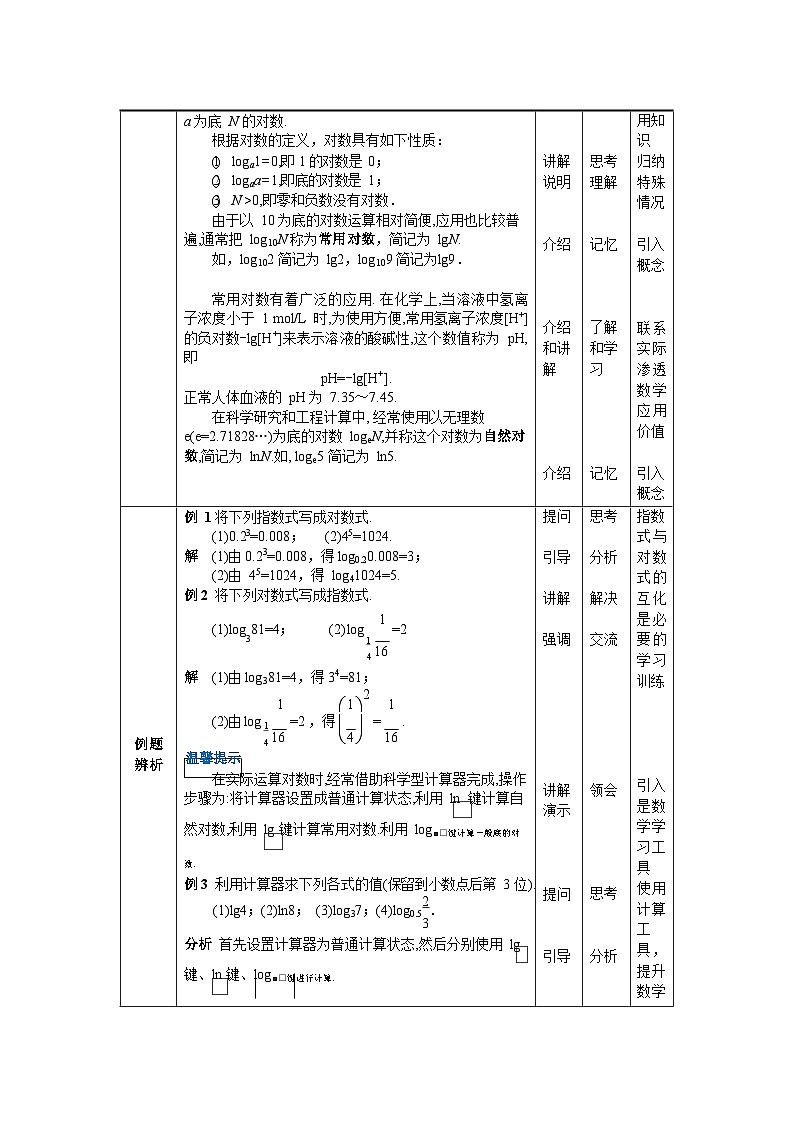
 a 为底 N 的对数.根据对数的定义，对数具有如下性质：(1)  loga1=0,即 1 的对数是 0；(2)  logaa=1,即底的对数是 1；(3)  N >0,即零和负数没有对数．由于以 10 为底的对数运算相对简便,应用也比较普遍,通常把 log10N 称为常用对数，简记为 lgN.如，log102 简记为 lg2，log109 简记为lg9． 常用对数有着广泛的应用. 在化学上,当溶液中氢离子浓度小于 1 mol/L 时,为使用方便,常用氢离子浓度[H+] 的负对数-lg[H+]来表示溶液的酸碱性,这个数值称为 pH, 即pH=-lg[H+].正常人体血液的 pH 为 7.35～7.45.在科学研究和工程计算中, 经常使用以无理数e(e=2.71828…)为底的对数 logeN,并称这个对数为自然对数,简记为 lnN.如, loge5 简记为 ln5.  讲解说明  介绍    介绍和讲解     介绍  思考理解  记忆    了解和学习     记忆用知识 归纳特殊情况 引入概念  联系实际渗透数学应用价值 引入概念               例题辨析例 1 将下列指数式写成对数式.(1)0.23=0.008； (2)45=1024.解 (1)由 0.23=0.008，得 log0.20.008=3；(2)由 45=1024，得 log41024=5.例 2 将下列对数式写成指数式. (1)log 81=4； (2) log 1 =23 14 16解 (1)由 log381=4，得 34=81；1  1 2 1(2)由log 1 =2 ，得     = .4 16  4  16温馨提示在实际运算对数时,经常借助科学型计算器完成,操作步骤为:将计算器设置成普通计算状态,利用 ln  键计算自然对数,利用 lg 键计算常用对数.利用 log■□键计算一般底的对数．例 3 利用计算器求下列各式的值(保留到小数点后第 3 位).(1)lg4；(2)ln8； (3)log37；(4)log0.52．3分析 首先设置计算器为普通计算状态,然后分别使用 lg键、ln 键、log■□键进行计算．提问 引导讲解强调       讲解演示    提问   引导思考 分析解决交流       领会     思考   分析指数式与对数式的互化是必要的学习训练     引入是数学学习工具 使用计算工 具， 提升数学
 解 (1)操作步骤为：按 lg→4→=,显示计算结果0.6020…,讲解演示强调操作解决交流运算核心素养所以 lg4≈0.602;同样地，通过计算器可算得其他各式的值：(2)ln8≈2.079；(3)log37≈1.771；(4)log0 2≈0.585．.53      巩固练习练习 5.3.11．将下列各指数式写成对数式.  (1) 23=8；(2) 0.53=0.125；(3) 5x=18.2．将下列各对数式写成指数式：(1) log0.110=-1;    (2) log8127 3 ; (3) log5  1  =-4.=4 6253．求下列对数的值：(1)log381 ;   (2) log0.80.8; (3) lg1; (4)lne.4．用计算器计算下列各式的值(保留到小数点后第 3位)．(1)lg4.5 ; (2) ln12; (3) log30.89.提问   巡视   指导思考   动手求解 交流及时掌握学生掌握情况查漏补缺  情境导入5.3.2 积、商、幂的对数20 世纪 30 年代,美国加州理工学院的地震学家里克特和古登堡提出了一种地震震级标度,以发生地震时产生的水平位移作为标准,即目前国际通用的里氏震级.里氏震级的计算公式为 M=lgA- lgA0，其中 A 表示地震的最大振幅,A0 表示“标准地震”的振幅.里氏震级的计算公式涉及对数运算的哪些运算法则.引导学生联系实际进行思考思考 分析   回答创设情境增加学生知识视野            探索新知设 M>0, N>0,a>0 且 a≠1,logaM=p, logaN=q,根据对数式和指数式的关系有ap=M，aq=N.因为MN ap·aq = ap+q ,所以,其对数式为loga(M·N)=p+q=logaM+logaN.又因为M         ap pq= =a ，N         aq所以,其对数式为log   M   p  q  log  M  log   N .a N a a同理,因为M n=(ap)n= apn(n 为任意实数)，所以logaMn=np=nlogaM.综上,对数运算有如下运算法则：(1) loga(M·N)=logaM+logaN；(2)  log   M = log   M  log   N ；a N a a(3) logaMn=nlogaM.讲解     说明         讲解     说明理解     记忆         思考     理解类比指数运算法则对照记 忆， 其次强化法则使用的条件
 其中, M>0, N>0,a>0 且 a≠1,n 为任意实数.          例题辨析例 4 用lgx, lgy, lgz 表示下列各式.x  y 3(1)lgx2y； (2)lg ； (3) lg x  lg   ．yz  x 解 (1) lgx2y=lgx2+lg y=2lgx+lgy；(2) lg  x   lg x  lg( yz) = lg x (lg y  lg z)yz= lg x  lg y  lg z; y 3 y(3) lg x  lg  x   = lg x  3lg x = lg x  3(lg y  lg x)=3lg y  2 lg x. 探究与发现如何将 log35 分别用常用对数和自然对数表示？提问 引导讲解强调    提出问题思考 分析解决交流    讨论交流巩固对数运算法 则， 强化知识发生过程  拓展学习   巩固练习练习 5.3.21.用 lgx, lgy, lgz 表示下列各式.(1) lg 3 x ； (2) lg(xy)  lg z ； (3) lg x y ．43 z2.计算下列各式的值.(1)log2(47×25)； (2)lne2．   3.设 a=ln2, b=ln3, 试用 a,b 表示ln  108 .提问   巡视   指导思考   动手求解 交流及时掌握学生掌握情况查漏补缺    归纳总结 引导 提问回忆 反思培养学生总结学习过程能力 布置作业1.书面作业：完成课后习题和学习与训练；2.查漏补缺：根据个人情况对课题学习复习与回顾;3.拓展作业：阅读教材扩展延伸内容.说明记录继续探究延伸学习