高中数学人教A版 (2019)必修 第一册2.1 等式性质与不等式性质同步训练题

这是一份高中数学人教A版 (2019)必修 第一册2.1 等式性质与不等式性质同步训练题，文件包含21一元二次函数方程和不等式-高一数学上学期同步精品讲义与分层练习人教A版必修第一册原卷版docx、21一元二次函数方程和不等式-高一数学上学期同步精品讲义与分层练习人教A版必修第一册解析版docx等2份试卷配套教学资源，其中试卷共22页， 欢迎下载使用。
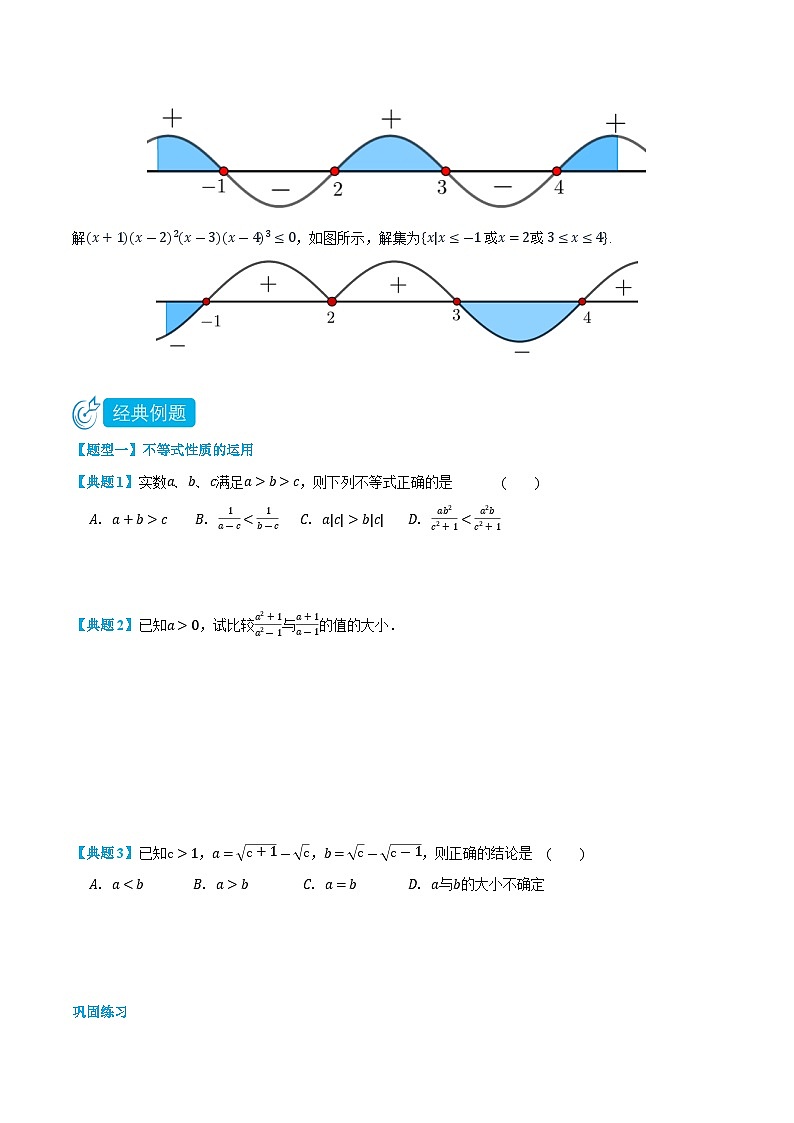
一元二次函数、方程和不等式1不等式关系与不等式① 不等式的性质(1) 传递性：；(2) 加法法则：；(3) 乘法法则：；     (4) 倒数法则：；(5) 乘方法则：；② 比较大小(1) 作差法(与的比较)(2) 作商法(与比较) 2 一元二次不等式及其解法① 二次函数的图象、一元二次方程的根、一元二次不等式的解集间的关系：(以下均以为例)函数、方程、表达式二次函数 
的图象一元二次方程的根有两个相异实数根有两个相等实数根没有实数根一元二次不等式的解集一元二次不等式的解集② 二次函数的图象、一元二次方程的根、一元二次不等式的解集间的关系，可充分利用二次函数图像去理解；③ 求解一元二次不等式时，利用二次函数图像思考，需要确定二次函数的开口方向，判别式，两根的大小与不等式的解集有关，而对称轴是不会影响解集的.3 一元二次不等式的应用(1) 分式不等式的解法解分式不等式可等价为有理整式不等式(组)求解.由于与均意味同号，故与等价的；与均意味异号，故与等价的；可得① ，且.比如且.② ，且.比如且.(2) 一元高次不等式的解法① 一元高次不等式通常先进行因式分解，化为(或)的形式，然后用穿针引线法求解.首先保证每个因式中的系数为正，然后从右侧画起，右侧第一个区间为正，从右向左依次正负出现，特别要注意“奇穿偶切”，“奇”(“偶”)指的是某个因式的次数.Eg 解，如图所示，解集为.解，如图所示，解集为. 【题型一】不等式性质的运用【典题1】实数满足，则下列不等式正确的是       (　　)       【解析】，错误，比如，得出；，，该选项正确；错误，比如时，；, 时，，，该选项错误．故选：．【点拨】涉及不等式的选择题，适当利用“取特殊值排除法”会做得更快些. 【典题2】已知，试比较与的值的大小．【解析】，(作差法)当时，，，则，即；(确定差)当时，，则，即．综上可得时，；时，．【点拨】比较两个式子的大小，可用做差法或做商法；一般幂的形式比较大小用作商法，比如比较与；多项式形式常用做差法，比如比较与. 【典题3】已知，，，则正确的结论是(　　)                   与的大小不确定【解析】方法一 特殊值法取特殊值，令，则，，易知, 排除，还不能排除，猜测选.方法二 做差法，分析法要比较大小，只需要比较的大小 (遇到二次根式可考虑平方去掉根号)而显然，故，故，故选.方法三 共轭根式法，，，，，即，故选.【点拨】① 比较两个式子的方法很多，选择题可以考虑取特殊值排除法；② 方法二中，遇到带有根号的常常两边平方去掉根号再比较，此时注意两个式子是否都是正数；在思考的过程中，不断使用“等价转化”把比较的两个式子越化越简单，等价过程中注意严谨；③ 方法三中注意到.若，互为共轭根式，它们的乘积、平方和差有一定的特点.. 巩固练习1 (★)  已知，那么下列不等式成立的是(　　)    【解析】，，，，．．．故选：．2 (★★)  设，则下列不等式恒成立的是(　　)                             【解析】设，可得，则错误；由可得，，可得，故错误；由可得1，则22，故正确；由，可得，故错误．故选：．3(★★) 已知，且，，则的关系是(　　)    【解析】因为，，且，，所以，，则0，当且仅当时取等成立，所以即，所以，故选：．4(★★) 若，，则，的大小关系是(　)                由的取值确定 【解析】，，，，∴，，且，，．故选．5(★★★) 设，则下列判断中正确的是(  )                    ．   【解析】即. 【题型二】二次函数、一元二次方程与一元二次不等式的关系  【典题1】 如果关于的不等式的解集为，则关于的不等式的解集为       .【解析】关于的不等式的解集为，是方程的两实数根，且，由韦达定理得，，不等式化为，即，解得或；则该不等式的解集为．【点拨】通过二次函数的图像理解，二次函数、一元二次方程和一元二次不等式三者之间的关系. 【典题2】解关于的不等式：【解析】；等价变形为：且； (注意分母)解得.  巩固练习1(★) 若不等式对一切实数都成立，则的取值范围为 (　　)    【答案】  【解析】对一切实数都成立，①时，恒成立，②时，，解可得综上可得，故选：．2(★★) 若关于的不等式的解集为，则等于(　)    【答案】 【解析】由题意知，和是方程的两个根，则由根与系数的关系，得，解得，所以．故选：．3(★★) 若不等式的解集是，则不等式的解集是(　)    【答案】   【解析】不等式的解集是()∪()，∴和是方程的两个实数根，由，解得：，， 故不等式即，即，解得：，所以所求不等式的解集是：，故选：．4(★★) 【多选题】关于的一元二次不等式的解集中有且仅有个整数，则的取值可以是(　　)    【答案】 【解析】设，其图象是开口向上，对称轴是的抛物线，如图所示；若关于的一元二次不等式0的解集中有且仅有个整数，则，即，解得，又，所以．故选：．5(★★) 不等式的解集是       . 6(★★) 已知不等式的解集是，，则不等式的解集是            .【答案】   【解析】不等式的解集是，则，是一元二次方程的实数根，且；，；不等式化为 ，；化为；又，；不等式的解集为：|}，故选：．7(★★) 不等式的解集为或，则值是    .【答案】 【解析】不等式等价于即，所以，解得，检验成立. 【题型三】求含参一元二次不等式角度1：按二次项的系数的符号分类，即;解不等式【解析】(不确定不等式对应函数是否是二次函数，分与讨论) 当时，不等式为，解集为； 当时， (二次函数与轴必有两个交点)解得方程两根；(二次函数的开口方向与不等式的解集有关，分与讨论)当时，解集为；当时, 解集为}.(注意的大小)综上，当时，解集为；当时，解集为；当时, 解集为}. 角度2：按判别式的符号分类解不等式.【解析】  (此时不确定二次函数是否与轴有两个交点，对判别式进行讨论)①当，即时，解集为；②当，即时，解集为；③当或，即时，此时两根为，显然，不等式的解集为或. 综上，当时，解集为；当时，解集为；当或时，解集为或.  角度3：按方程的根大小分类解不等式：.【解析】原不等式可化为：令，得；(因式分解很关键，此时确定与轴有交点，的大小影响不等式解集)当时，即时，解集为；当时，即或时，解集为；当时，即或时，解集为}.综上，当时，解集为；当或时，解集为；当或时，解集为}.【点拨】① 当求解一元二次不等式时，它是否能够因式分解，若可以就确定对应的二次函数与轴有交点，就不需要考虑判别式.常见的形式有，等，若判别式是一个完全平方式，它就能做到“较好形式的十字相乘”，当然因式分解也可以用公式法求解；② 在求解含参的一元二次不等式，需要严谨，多从二次函数的开口方向、判别式、两根大小的比较三个角度进行分类讨论，利用图像进行分析. 巩固练习1 (★★)  关于的不等式的解集中恰有个整数，则实数的取值范围是    (　　)   【答案】 【解析】由，得，若，则不等式无解．若，则不等式的解为，此时要使不等式的解集中恰有个整数解，则此时个整数解为，则．若，则不等式的解为，此时要使不等式的解集中恰有个整数解，则此时个整数解为，则．综上，满足条件的的取值范围是．故选：．  2 (★★)  解关于的不等式 ．【答案】时，不等式的解集是，  时，不等式的解集是，  时，不等式的解集是．【解析】方程中，①当即时，不等式的解集是，②当，即时，不等式的解集是，③当即时，由解得：，时，不等式的解集是，综上，时，不等式的解集是，时，不等式的解集是，时，不等式的解集是．3 (★★) 解关于的不等式：．【答案】 或时，不等式的解集为；时，不等式的解集为；时，不等式的解集为．    【解析】关于的不等式：中，，当或时，，对应的一元二次方程有两个实数根和，且，不等式的解集为或x}；当时，，对应的一元二次方程有两个相等的实数根，不等式的解集为}；当时，，不等式的解集为；综上，或时，不等式的解集为；时，不等式的解集为；时，不等式的解集为．   4(★★★) 若，解关于的不等式．【答案】当时，解集是；  当时，解集是；  当时，解集是；当时，解集是．    【解析】当时，．                                              当a≠0时，．当时，，解得．                 当时，．当时，                                              当时，，或．当时，，或．                                     当时，解集是；当时，解集是；当时，解集是；当时，解集是．   5 (★★★) 关于的不等式恰有个整数解，求实数的取值范围.答案】  【解析】不等式恰有个整数解，即恰有两个解，，即，或．当时，不等式解为，，恰有两个整数解，即：，，，解得：；当时，不等式解为，，恰有两个整数解即：，，，解得，综上所述：，或．