人教版八年级上册11.2.1 三角形的内角课堂教学ppt课件

这是一份人教版八年级上册11.2.1 三角形的内角课堂教学ppt课件，共22页。PPT课件主要包含了一个内角是60°，三边都不相等三角形，等腰三角形，方法一测量法，方法二折叠法，方法三拼凑法，①等边三角形，②三边都不相等三角形，③等腰三角形，钝角三角形等内容，欢迎下载使用。

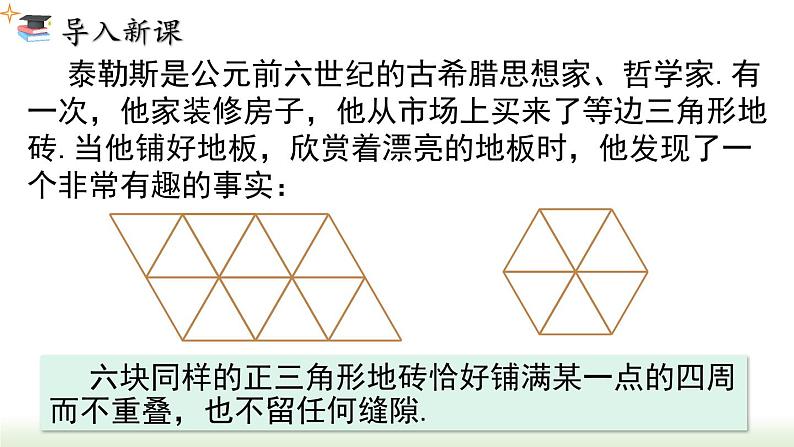
泰勒斯是公元前六世纪的古希腊思想家、哲学家.有一次，他家装修房子，他从市场上买来了等边三角形地砖.当他铺好地板，欣赏着漂亮的地板时，他发现了一个非常有趣的事实：
六块同样的正三角形地砖恰好铺满某一点的四周而不重叠，也不留任何缝隙.
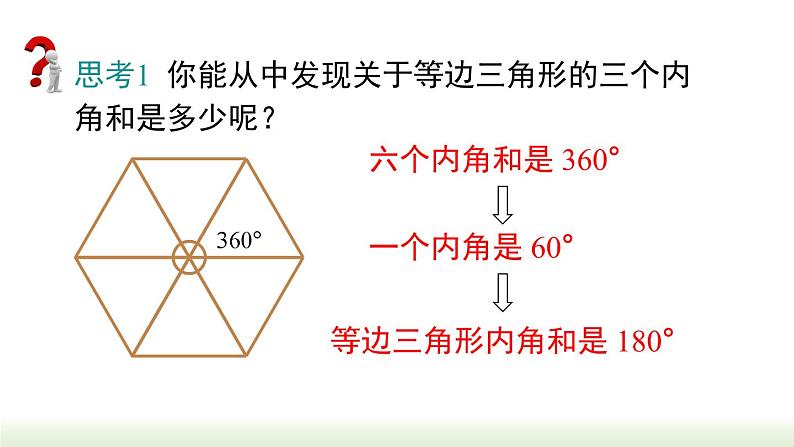
思考1 你能从中发现关于等边三角形的三个内角和是多少呢？
等边三角形内角和是 180°
六个内角和是 360°
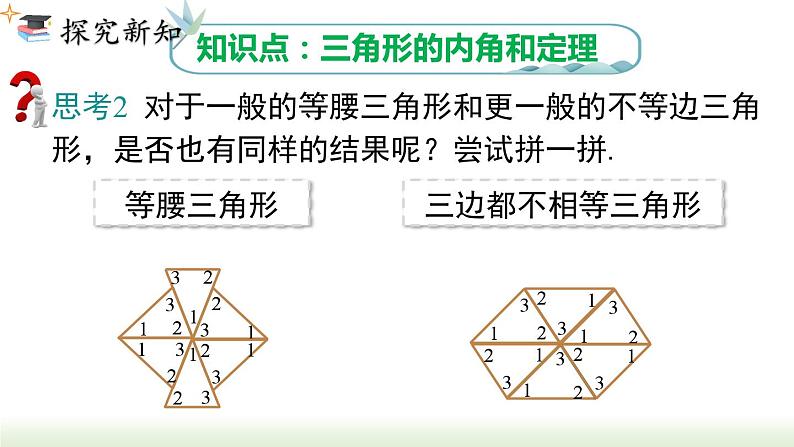
知识点：三角形的内角和定理
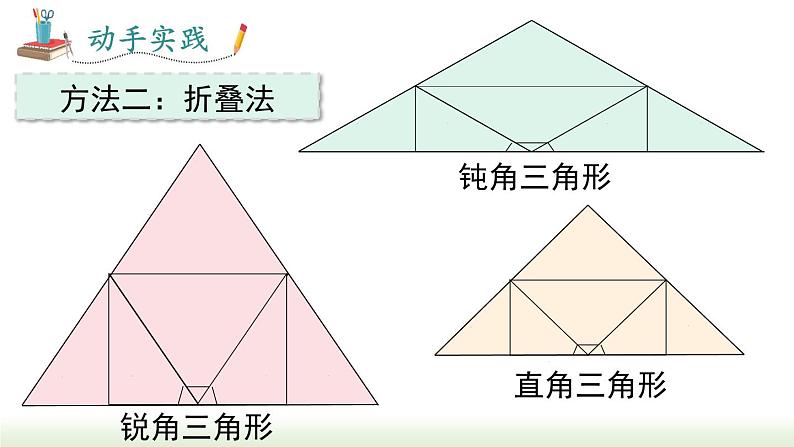
思考2 对于一般的等腰三角形和更一般的不等边三角形，是否也有同样的结果呢？尝试拼一拼.
分组证明：“任意一个三角形的内角一定等于 180° ”.
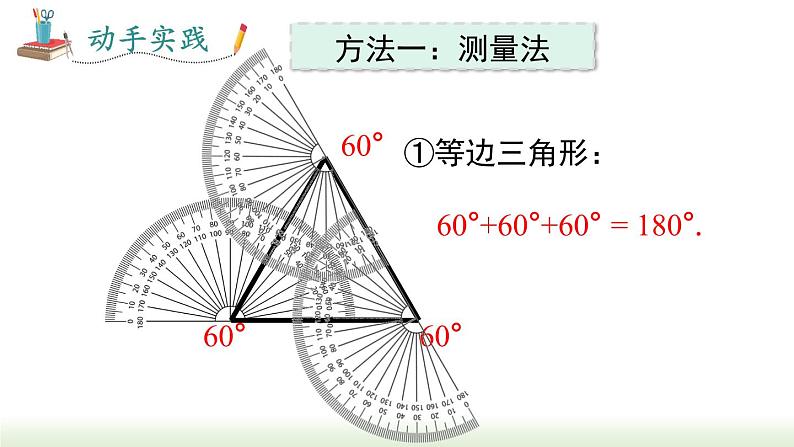
60°+60°+60° = 180°.
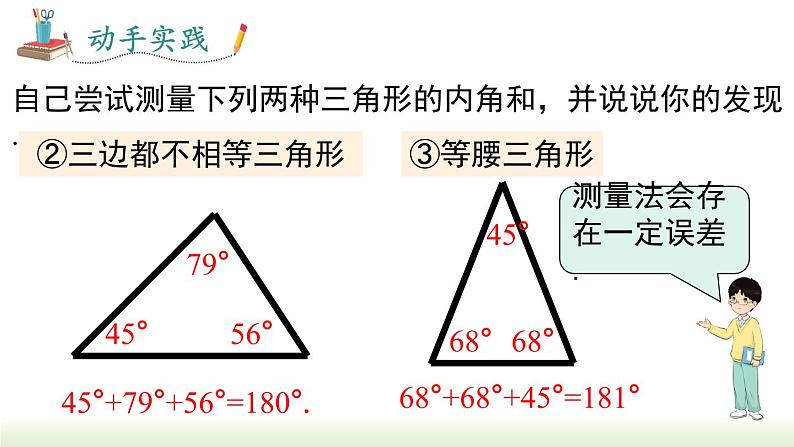
自己尝试测量下列两种三角形的内角和，并说说你的发现.
测量法会存在一定误差.
45°+79°+56°=180°.
68°+68°+45°=181°
观测的结果不一定可靠，还需要通过数学知识来证明.从上面的操作过程，你能发现证明的思路吗？
求证：∠A +∠B +∠C = 180°.
证法1：过点 A 作 l∥BC，则∠B =∠1，∠C =∠2 (两直线平行，内错角相等). ∵∠1 +∠2 +∠BAC = 180°，∴∠B +∠C +∠BAC = 180°.
证法2：延长 BC 到 D，过点 C 作 CE∥BA，则∠A =∠1(两直线平行，内错角相等)， ∠B =∠2(两直线平行，同位角相等).又∵∠1 +∠2 +∠ACB = 180°，∴∠A +∠B +∠ACB = 180°.
证法3：过 D 作 DE∥AC，DF∥AB.∴∠C = ∠EDB，∠B = ∠FDC(两直线平行，同位角相等)，∠A +∠AED = 180°，∠EDF +∠AED = 180°(两直线平行，同旁内角相补).∴∠A = ∠EDF.∵∠EDB +∠EDF +∠FDC = 180°，∴∠C +∠A +∠B = 180°.
想一想：同学们还有其他的证法吗？
思考3 多种方法证明三角形内角和等于 180° 的核心是什么？
转化思想：将三个角转化到一个平角上.
三角形内角和定理：三角形三个内角的和等于 180°.
例1 如图，在△ABC 中， ∠BAC = 40°，∠B = 75°，AD 是△ABC 的角平分线，求∠ADB 的度数.
在△ABD 中，∠ADB = 180° - ∠B - ∠BAD = 180° - 75° - 20° = 85°.
解：由∠BAC = 40°， AD 是△ABC 的角平分线，得
例2 如图，C 岛在 A 岛的北偏东 50°方向，B 岛在 A 岛的北偏东 80°方向，C 岛在 B 岛的北偏西 40°方向. 从 B 岛看 A，C 两岛的视角∠ABC 是多少度？从 C 岛看 A，B 两岛的视角∠ACB 呢？
分析：求 ∠ACB，需先求 ∠CAB 、∠CBA.
解：由题意得∠CAB =∠BAD -∠CAD = 80° - 50° = 30°.
由 AD∥BE，得∠BAD + ∠ABE = 180°，
所以∠ABE = 180° - ∠BAD = 180° - 80° = 100°， ∠ABC = ∠ABE - ∠EBC = 100° - 40° = 60°.
在△ABC 中，∠ACB = 180 °- ∠ABC - ∠CAB = 180°- 60°- 30° = 90°.
答：从 B 岛看 A，C 两岛的视角∠ABC 是 60°，从 C 岛看 A，B 两岛的视角∠ACB 是 90°.
1.(长春)如图，在 △ABC 中，CD 平分∠ACB 交 AB 于点 D，过点 D 作 DE∥BC 交 AC 于点 E.若∠A = 54°，∠B = 48°，则 ∠CDE 的大小为 ( )A.44°B.40°C.39°D.38
∠A = 54°，∠B = 48°
∠ACB = 78°
∠CDE = ∠DCB = 39°
_____思想：将是三个角转化成一个_____或者同旁内角____等
三角形的三个内角和等于____
1. 求出下列各图中的 x 值.
2.(大庆)如图，在△ABC 中，∠A = 40°，D 点是∠ABC 和 ∠ACB 角平分线的交点，则∠BDC = ______.
∠ABC + ∠ACB = 140°
D 点是角平分线的交点