初中数学人教版八年级上册13.3.1 等腰三角形课前预习ppt课件

这是一份初中数学人教版八年级上册13.3.1 等腰三角形课前预习ppt课件，共20页。PPT课件主要包含了等腰三角形，两底角相等，三线合一，一底角，一底边，方法一构造等角，构造两个全等三角形，证明边相等，∴ABAC，几何语言等内容，欢迎下载使用。

小马虎在设计一个等腰△ABC (AB = AC) 的房梁时，一不小心，它的一部分被墨水涂没了，只留下底边 BC 和一个底角∠C，同学们想一想，有没有办法把原来的等腰△ABC 重新画出来?大家试试看.
知识点:等腰三角形的判定
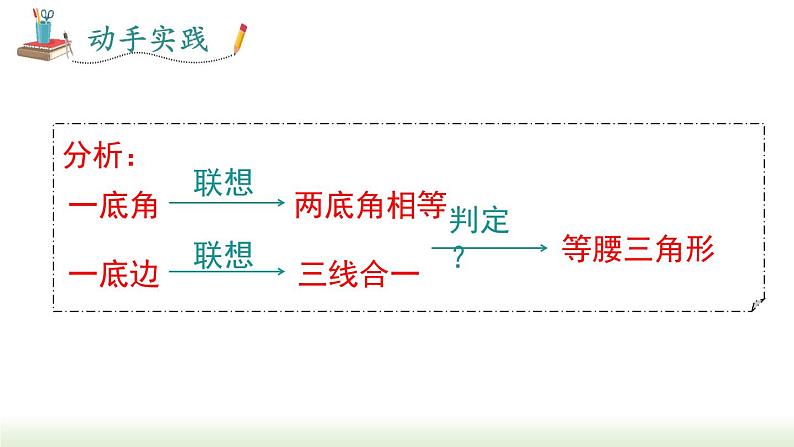
如图，已知底边 BC 和∠C，请分组补全等腰△ABC.
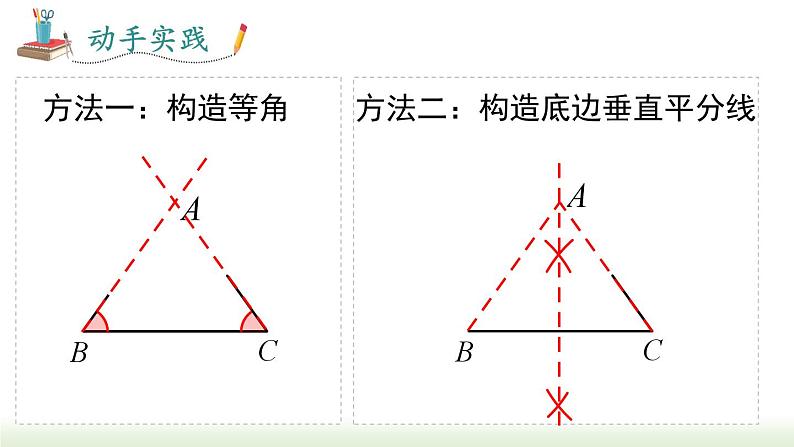
方法二：构造底边垂直平分线
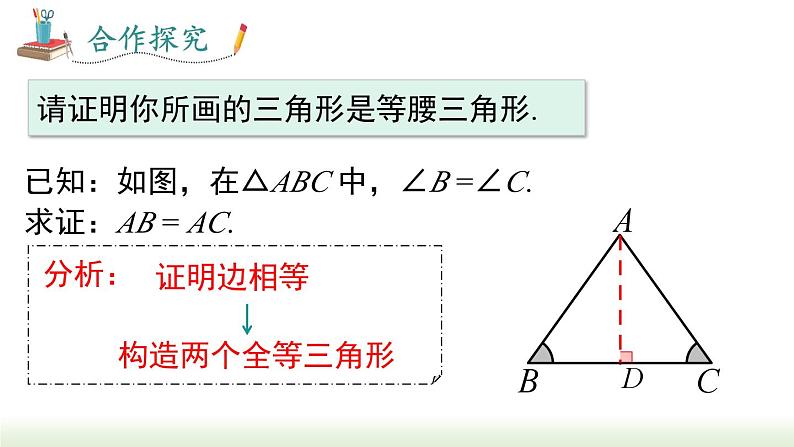
请证明你所画的三角形是等腰三角形.
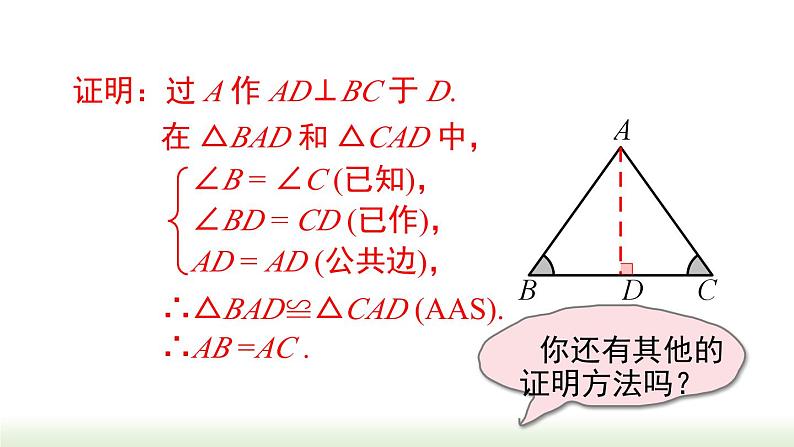
已知：如图，在△ABC 中，∠B =∠C.求证：AB = AC.
∠B = ∠C (已知)，
∠BD = CD (已作)，
AD = AD (公共边)，
∴△BAD≌△CAD (AAS).
在 △BAD 和 △CAD 中，
证明：过 A 作 AD⊥BC 于 D.
你还有其他的证明方法吗？
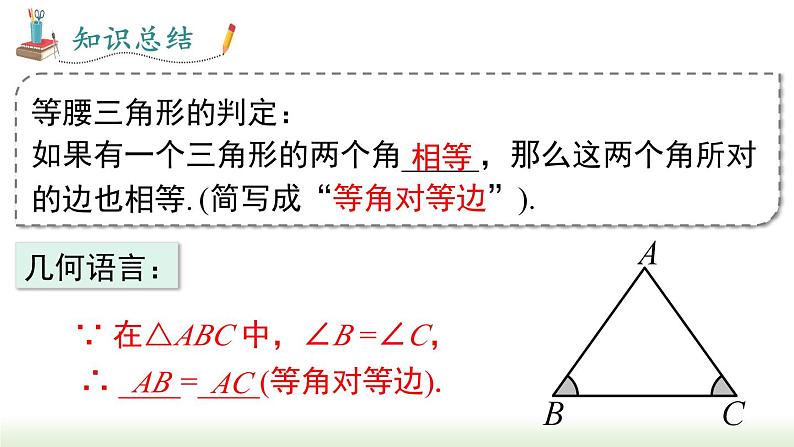
等腰三角形的判定：如果有一个三角形的两个角_____，那么这两个角所对的边也相等.
(简写成“等角对等边”).
∵ 在△ABC 中，∠B =∠C，
∴ ____=____(等角对等边).
已知如图，在 △ABC 中，∠A = 20°，∠B = 80°，AB = 6，AC = 2BC.
(1) △ABC 的边 AC 的长度为_____； (2) △ABC 的周长是______.
例1 求证：如果三角形一个外角的平分线平行于三角形的一边，那么这个三角形是等腰三角形.
已知：如图，∠CAE 是△ABC 的外角，∠1 =∠2，AD∥BC. 求证：AB = AC.
先证明 ∠B = ∠C
利用∠1 =∠2，AD∥BC
∴ AB = AC(__________)．
∴∠1 =∠B (_______________________)， ∠2 =∠C (_______________________)．
证明： ∵ AD∥BC，
两直线平行，同位角相等
两直线平行，内错角相等
证明两条线段相等，除了证明线段所在两个三角形全等外，还可以判定两条线段所在三角形是等腰三角形.
∴∠B =∠C，
例2 已知等腰三角形底边长为 a，底边上的高的长为 h，求作这个等腰三角形.
(1) 作线段 AB = a；
(4) 连接 AC，BC，则△ABC 即为所求.
(3) 在 MN 上取一点 C，使 DC = h；
(2) 作线段 AB 的垂直平分线 MN，交 AB 于点 D；
1.两个底角____2.两条边____
1.下列选项中，不能判定△ABC 是等腰三角形的是 ( )A.∠B = 45°，∠C = 90° B.∠B = 120°，∠C = 30°C.∠B = 70°，∠C = 40° D.∠B = 50°，∠C =60°
2. 如图，已知 OC 平分∠AOB，CD∥OB，若 OD＝3 cm，则 CD 的长为 ________.
3. 已知如图，四边形 ABCD 是一个等腰梯形，BD平分∠ABC，BC = 9 cm，若 AD = 5 cm，则四边形ABCD的周长为________.
4. (淄博)如图，在△ABC 中，∠ABC 的平分线交 AC 于点 E .过点 E 作 DE∥BC 交 AB 于点 D.(1) 求证：DB = DE；(2) 若 ∠A = 80°，∠C = 40°，求∠DEB 的度数.
∴∠ABE =∠CBE = ∠ABC = 30°.
解：(1)证明：在 △ABC 中，∠ABC 的平分线交 AC 于点 E，
由(1)知∠DEB =∠DBE = 30°.故∠DEB 的度数为 30°.
∴∠ABC 的平分线交 AC 于点 E.
∴∠ABC = 60°.
(2)∵∠A = 80°，∠C = 40°，
∴∠DEB =∠DBE. ∴DB = DE.
∴∠DEB =∠CBE.
∴∠ABE =∠CBE.
5.综合与实践【问题情境】数学活动课，老师带领同学们开展“测量塔高”的实践活动(同学们的身高忽略不计，且塔楼不阻碍通行)
【实践发现】如图，小明根据已有的数学知识，制订了测量步骤，并将测量数据记录如下。① 选取塔的顶端作为参照点 A；② 地面直线 l 上取测量点 C，在 C 处用工具测得∠ACD = 45°；③ 沿射线 CB 的方向行走至测量点 D ，点 D 和点 C 在塔的两侧，并在 D 处用工具测得 ∠ADC = 45°；④ 测得行走距离 CD ≈ 81.2 米.【问题解决】请你根据小明的测量步骤，求出塔高 AB 的长度.