人教版八年级上册13.4课题学习 最短路径问题课文内容ppt课件

这是一份人教版八年级上册13.4课题学习 最短路径问题课文内容ppt课件，共17页。PPT课件主要包含了未知问题，同侧两点最短，已知问题，异侧两点最短，同侧转化异侧，实际问题，数学问题，湖岸l₁，解如图2示，AM+NB等内容，欢迎下载使用。
相传，古希腊亚历山大里亚城里有一位久负盛名的学者，名叫海伦.有一天，一位将军专程拜访海伦，求教一个百思不得其解的问题：从图 1 中的 A 地出发，到一条笔直的河边 l 饮马，然后到 B 地.到河边个么地方饮马可使他所走的路线全程最短?
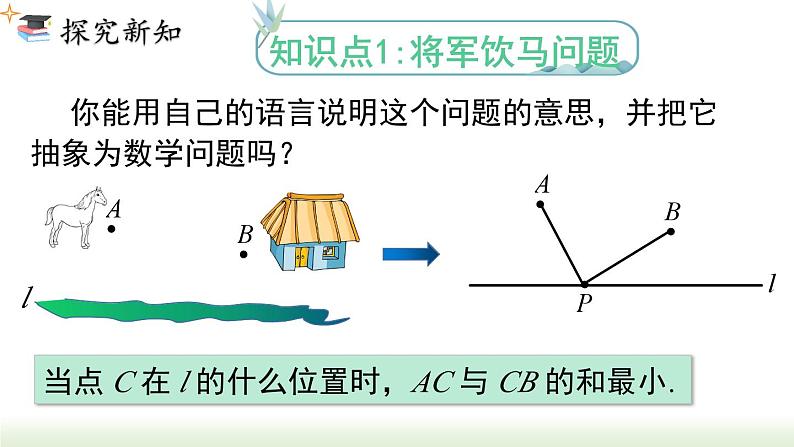
知识点1:将军饮马问题
你能用自己的语言说明这个问题的意思，并把它抽象为数学问题吗？
当点 C 在 l 的什么位置时，AC 与 CB 的和最小.
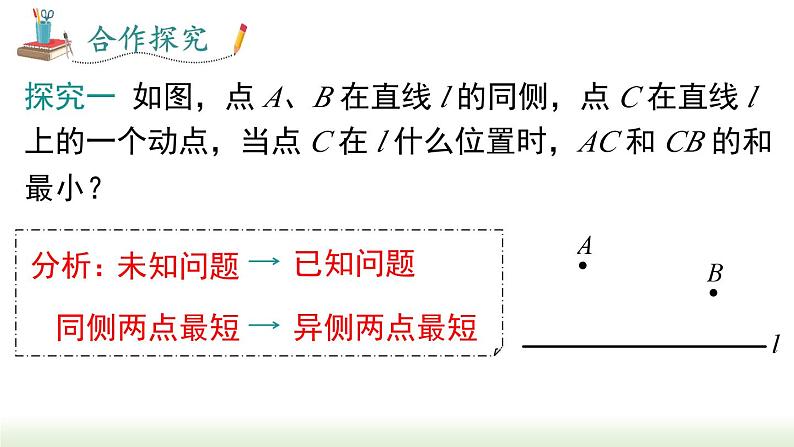
探究一 如图，点 A、B 在直线 l 的同侧，点 C 在直线 l 上的一个动点，当点 C 在 l 什么位置时，AC 和 CB 的和最小？
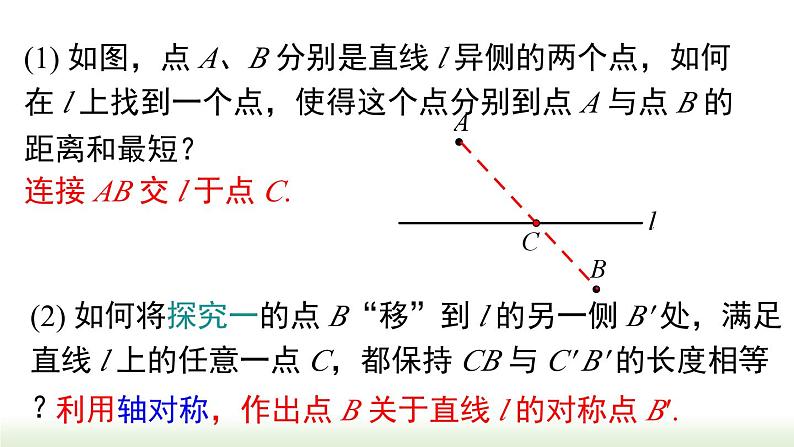
(1) 如图，点 A、B 分别是直线 l 异侧的两个点，如何在 l 上找到一个点，使得这个点分别到点 A 与点 B 的距离和最短？
连接 AB 交 l 于点 C.
(2) 如何将探究一的点 B“移”到 l 的另一侧 B′ 处，满足直线 l 上的任意一点 C，都保持 CB 与 C′ B′ 的长度相等？
利用轴对称，作出点 B 关于直线 l 的对称点 B′.
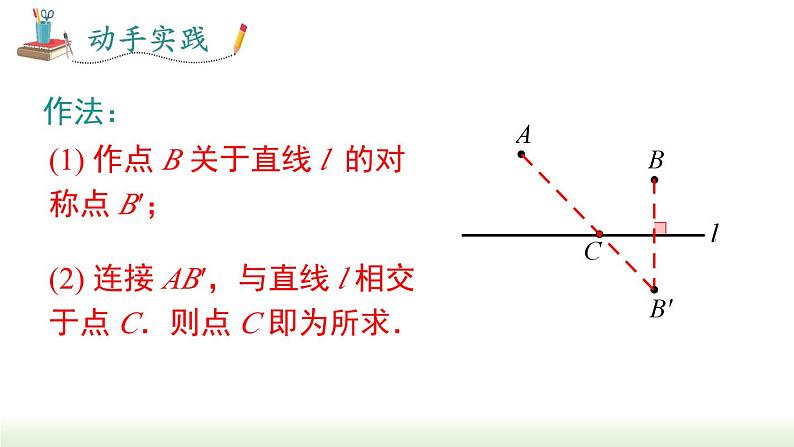
(1) 作点 B 关于直线 l 的对称点 B′；
(2) 连接 AB′，与直线 l 相交于点 C．则点 C 即为所求．
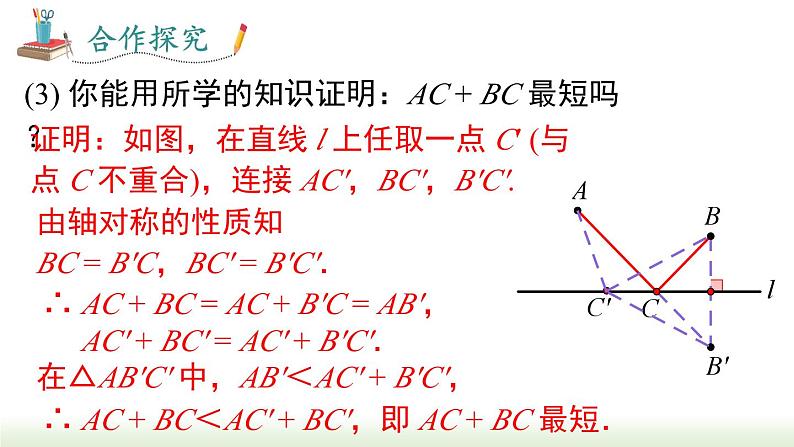
(3) 你能用所学的知识证明：AC + BC 最短吗？
证明：如图，在直线 l 上任取一点 C′ (与点 C 不重合)，连接 AC′，BC′，B′C′.
由轴对称的性质知 BC = B′C，BC′ = B′C′．
∴ AC + BC = AC + B′C = AB′， AC′ + BC′ = AC′ + B′C′．
在△AB′C′ 中，AB′＜AC′ + B′C′，
∴ AC + BC＜AC′ + BC′，即 AC + BC 最短．
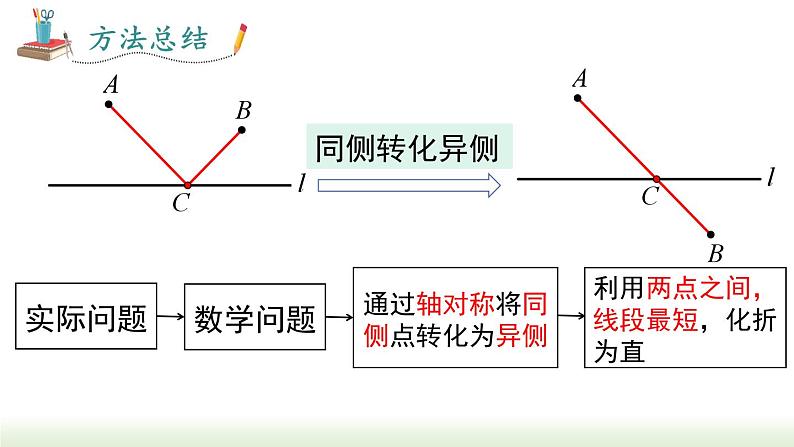
通过轴对称将同侧点转化为异侧
利用两点之间，线段最短，化折为直
1.如图 (1) 是示意图，游船从湖岸 l₁ 的码头 D 将游客送往亭子 M 停留观赏，然后将游客送往湖岸 l₂ 的码头 C，最后再回到码头 D.请在图 (2) 中画出游船的最短路径，并确定两个码头的位置(练一练 2 超链接).
知识点2:造桥选址区问题
探究二 如图，A 和 B 两地在一条河的两岸，现要在河上造一座桥 MN. 桥造在何处可使从 A 到 B 的路径 AMNB 最短(假定河的两岸是平行的直线，桥要与河垂直)？
当点 N 在直线 b 的什么位置时，AM+MN+NB 最小？
A′N + NB 最短
A′、N、B 三点共线
2.如图 (1) 是示意图，在第 1 题的条件下，如果在湖面上再新建一座观赏亭 N，且游船路线为湖岸 l₁ 的码头 D→亭子 M→亭子 N→湖岸 l2 的码头 C→湖岸 l₁ 的码头 D.请在图(2)中画出游船的最短路径，并确定两个码头的位置.(提示：思考最短路线是由哪几条线段相加).
通常利用________、________实现线段的转移，把已知问题转化成容易解决的问题
1.(佛山校考)某开发商的经适房的三个居民小区 A、B、C 在同一条直线上，位置如图所示，其中小区 B 到小区A、C 的距离分别是 70 m 和 150 m，小区 A、C 之间建立一个超市，要求各小区居民到超市总路程和最小，那么超市的位置应建在 ( )A.小区 AB. 小区 BC.小区 CD. AC 的中点
2.线段 AC 是正方形 ABCD 的对角线，点 M 是边 CD 上的一定点(不与 D，C 重合)，请在对角线 AC 上找一点 P，使得△PDM 的周长最小，并作简要说明．
解：如图，连接 BM，
交 AC 于点 P，点 P 即为所求．