人教版八年级上册第十五章 分式15.3 分式方程课堂教学课件ppt

这是一份人教版八年级上册第十五章 分式15.3 分式方程课堂教学课件ppt，共20页。PPT课件主要包含了实际问题，设未知数，列出方程，检验解的合理性，解方程，找等量关系，两队合作完成的工作量，甲队单独完成的工作量，方法一，方法二等内容，欢迎下载使用。

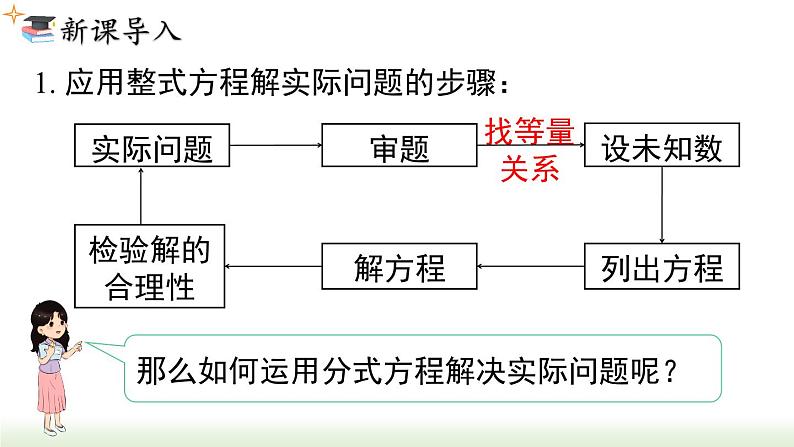
1. 应用整式方程解实际问题的步骤：
那么如何运用分式方程解决实际问题呢？
知识点1：列分式方程解决工程问题
探究一 ：两个工程队共同参与一项筑路工程，甲队单独施工 1 个月完成总工程的三分之一，这时增加了乙队，两队又共同工作了半个月，总工程全部完成，哪个队的施工速度快？
分析：审题 → 找等量关系
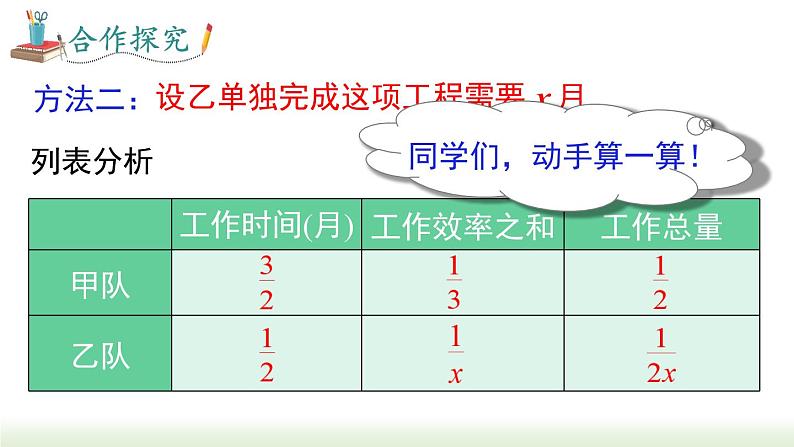
请同学们列出分式方程解决这个问题吧！
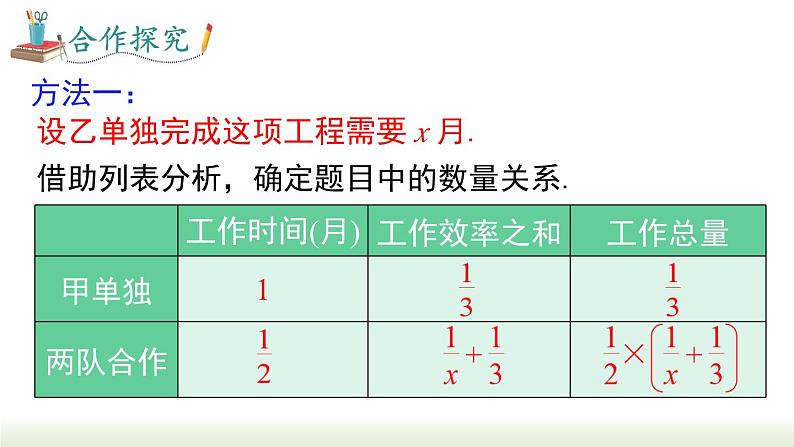
设乙单独完成这项工程需要 x 月.
借助列表分析，确定题目中的数量关系.
解：设乙单独完成这项工程需要 x 月，则乙队的工作效率是 ，记总工程量为 1，根据工程的实际进度，得
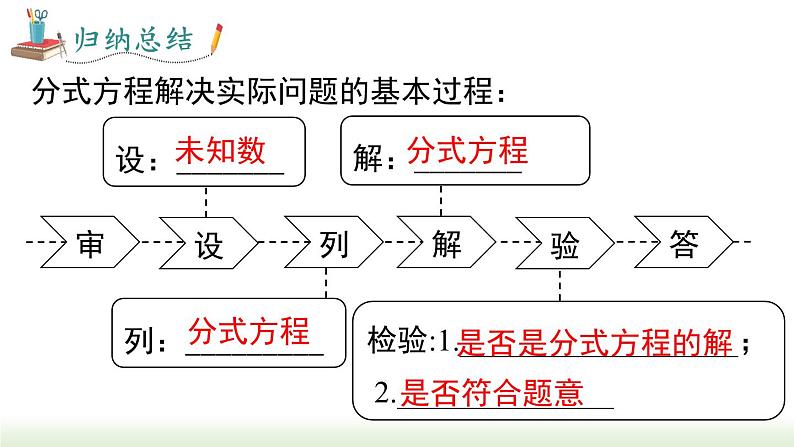
列：_________
检验:1.__________________； 2.______________
分式方程解决实际问题的基本过程：
1. (武汉开学考)张明 3 小时清点完一批图书的一半，李强清点另一半图书的工作，两人合作 小时清点完另一半图书. 如果李强单独清点这批图书需要几个小时？
经检验 x = 4 是原方程的解.
答：李强单独清点完这批图书需要 4 个小时.
知识点2：列分式方程解决行程问题
探究二 ：某次列车平均提速 v km/h．用相同的时间，列车提速前行驶 s km，提速后比提速前多行驶 50 km，提速前列车的平均速度为多少？
行程问题：路程 = 速度×时间
类比探究一方法分析下这道题
提速后的行驶时间 = 提速前的行驶时间
设提速前列车的平均速度为 x km/h，其中s，v是已知值.
解：提速前列车的平均速度为 x km/h， 依题意得
2. (广州期末)已知从 A 地到某市的高铁行驶路程是 400 千米，普通列车的行驶路程是高铁行驶路程的 1.3 倍，若高铁的平均速度 (千米/时) 是普通列车平均速度 (千米/时) 的 2.5 倍，且乘坐高铁所需时间比乘坐普通列车所需时间缩短 3 小时，求普通列车和高铁的平均速度.
解：设普通列车平均速度是 x 千米/小时，则高铁平均速度是 2.5x 千米/小时，根据题意，得
解得 x = 120.
经检验 x = 120 是原方程的根，且符合题意，
答：普通列车的平均速度是 120 千米/小时，高铁的平均速度为 300 千米/小时.
2.5x = 120×2.5 = 300 千米/小时
知识点3：列分式方程解决利润问题
探究三 ： (长治阶段考)“四书五经”是一部被中国人读了几千年的教科书，是我们了解中国古代社会的一把钥匙. 某学校计划分阶段引导学生读这些书，决定先购买《论语》和《孟子》供学生阅读，已知用 1000 元购买《孟子》的数量是用 800 元购买《论语》的数量的 2 倍，《孟子》的单价比《论语》的单价少 15 元.则《论语》和《孟子》的单价各是多少元?
解：设《孟子》的单价为 x 元，则《论语》的单价为 ( x + 15 ) 元.
解得 x = 25.
经检验 x = 25 是原方程的解，且符合题意，
∴ x + 15 = 25 + 15 = 40 .
答：《论语》和《孟子》的单价分别是 40 元和 25 元.
1. 几名同学包租一辆面包车去旅游，面包车的租价为 180 元，出发前，又增加两名同学，结果每个同学比原来少分摊 3 元车费，若设原来参加旅游的学生有 x 人，则所列方程为 (　　)
2. 一轮船往返于 A、B 两地之间，顺水比逆水快 1 小时到达.已知 A、B 两地相距 80 千米，水流速度是 2 千米/时，求轮船在静水中的速度.
解：设船在静水中的速度为 x 千米/时,根据题意得
解得 x = ±18.
检验：当 x = －18 时，不符合题意，舍去；而 x = 18 是原方程的根，且符合题意. 所以 x = 18.
答：轮船在静水中的速度为 18 千米/时.