初中数学人教版八年级上册12.2 三角形全等的判定背景图课件ppt

这是一份初中数学人教版八年级上册12.2 三角形全等的判定背景图课件ppt，共19页。PPT课件主要包含了测量AB长度，实现边的转移，利用三角形全等，如何构造呢，问题转化，两边的夹角，其中一边的对角，3连接BC，是两边的“夹角”，几何语言等内容，欢迎下载使用。

如图，有一池塘，要测池塘两端 A、B 的距离，如何测出呢(假设池塘足够宽)？
你会采取什么样的测量方法呢？
如何测出呢(假设池塘足够宽)？
思考一 已知两条边对应相等，能否加上一个角相等证明两个三角形全等呢？这个角是否具有一定的特殊性？
已知两条边，和一个角，能否画出唯一的一个三角形？
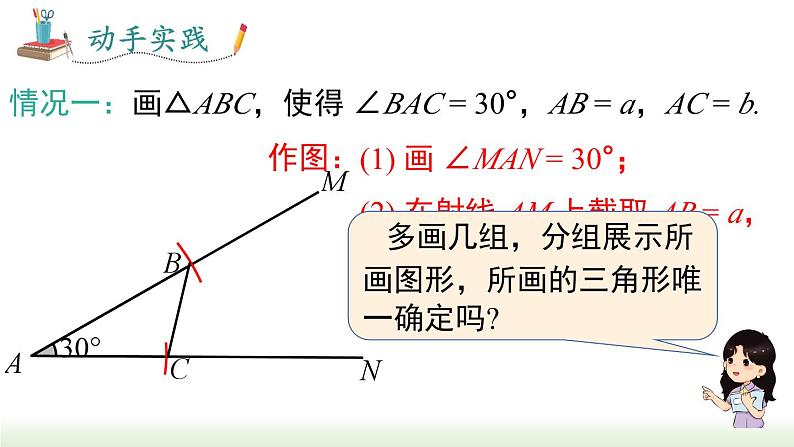
情况一：画△ABC，使得 ∠BAC = 30°，AB = a，AC = b.
(2) 在射线 AM 上截取 AB = a，在射线 AM 上截取 AC = b ；
(1) 画 ∠MAN = 30°；
多画几组，分组展示所画图形，所画的三角形唯一确定吗?
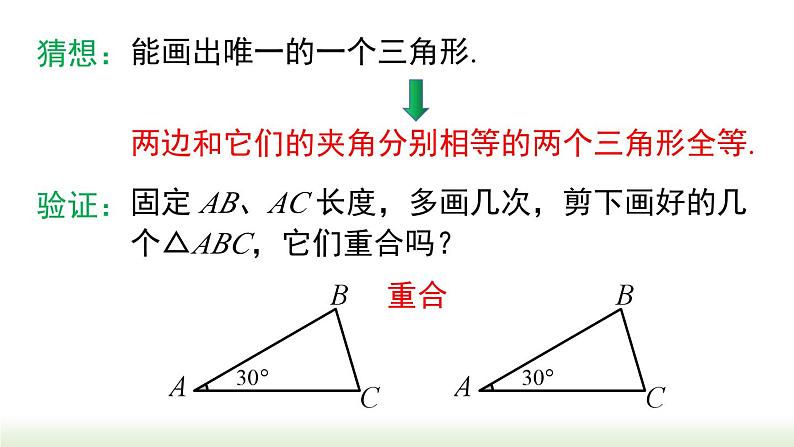
能画出唯一的一个三角形.
固定 AB、AC 长度，多画几次，剪下画好的几个△ABC，它们重合吗？
两边和它们的夹角分别相等的两个三角形全等.
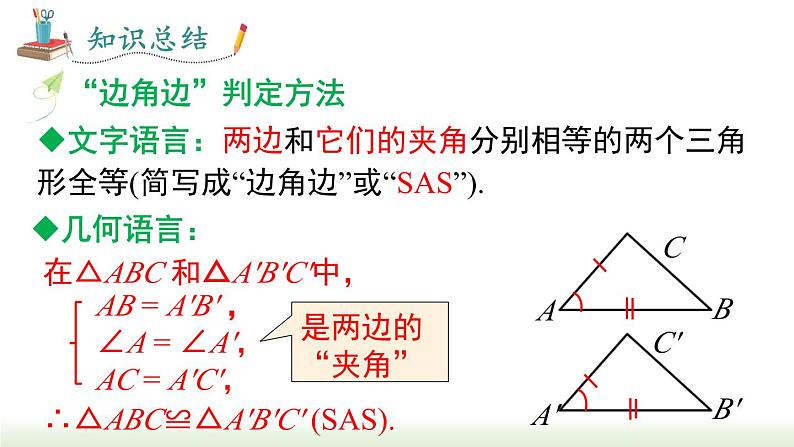
在△ABC 和△A′B′C′中，
∴△ABC≌△A′B′C′ (SAS).
文字语言：两边和它们的夹角分别相等的两个三角形全等(简写成“边角边”或“SAS”).
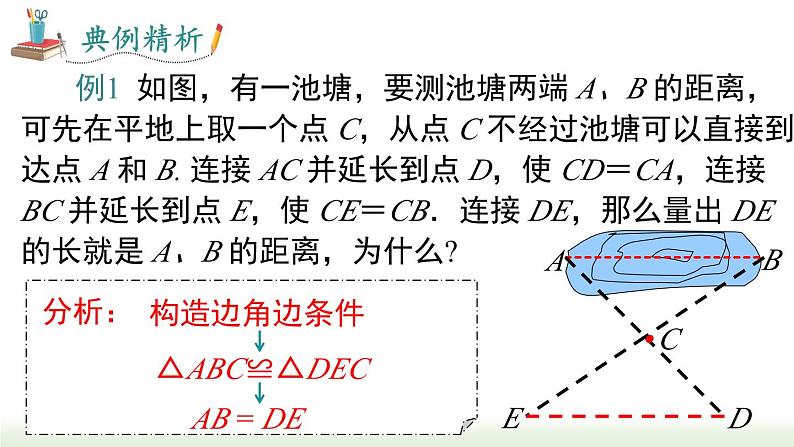
例1 如图，有一池塘，要测池塘两端 A、B 的距离，可先在平地上取一个点 C，从点 C 不经过池塘可以直接到达点 A 和 B. 连接 AC 并延长到点 D，使 CD＝CA，连接 BC 并延长到点 E，使 CE＝CB．连接 DE，那么量出 DE 的长就是 A、B 的距离，为什么?
解：在△ABC 和△DEC 中，
∴△ABC≌△DEC (SAS).∴ AB = DE (全等三角形的对应边相等).
1. (烈山区期末)如图，在△ABC 中，AB = AC，点 D，E 分别是 AB 、AC 的中点，求证：△ACD≌△ABE .
证明：∵点 D，E 分别是 AB 、AC 的中点
在△ACD 和△ABE 中，
∴△ACD≌△ABE(SAS).
先假设一个固定值，AB = 6，AC = 8
情况二：画△ABC，使得 ∠ACB = 30°，AB = a，AC = b.
(2) 在射线 CM 上截取CA= 8，以 A 为圆心，6 为半径画弧，交 CN 于点 B；
(1) 画 ∠MCN= 30°；
多画几组，分组展示所画图形，所画的三角形唯一确定吗?
1.两边和它们的夹角分别相等的两个三角形全等；2.两边和其中一边的对角分别相等不能判定全等.
关于第二种情况的深入探究见本节课后的课外探究.
2. 如图，某海岸线沿线有 A， B 两个码头，在该海域内有两座小岛 C，D，航线 AC 与 BD 交汇于点 O，经测量，AC = BD，OA = OB，求证 ∠ADB = ∠BCA.
证明：∵AC = BD，OA = OB，∴ AC - OA = BD - OB， 即 OC = OD.
在△AOD 和△BOC 中，
∴△AOD≌△BOC (SAS).
∴ ∠ADB = ∠BCA.
为证明三角形全等提供新的证明方法
1.已知两边，必须找“夹角”2. 已知一角和这角的一夹边，必须找这角的另一夹边
1. 如图，已知 AB∥CD，AB = CD ，AE = FD，则下列结论中： ①△ABE≌△CDF；②△ABF≌△CDE；③BE∥DF； 正确的有 ______ .
2.如图，AC = BD，∠CAB =∠DBA，求证：BC = AD.
证明：在△ABC 与△BAD 中
AC = BD (已知)， ∠CAB =∠DBA (已知)， AB = BA (公共边)，
∴ △ABC≌△BAD (SAS).
∴ BC = AD(全等三角形的对应边相等).
3.小张做了一个如图所示的风筝，其中∠EDH =∠FDH，ED = FD ，将上述条件标注在图中，小张不用测量就能知道 EH = FH 吗？与同桌进行交流.
ED＝FD (已知)，　 ∠EDH＝∠FDH (已知)，　 DH＝DH (公共边)，
∴ △EDH≌△FDH (SAS).
解：能. 在△EDH 和△FDH 中，
画△ABC，使得 ∠ABC = 30°，AB = a，BC = b.固定 AB 长度，根据 AC 的不同取值范围，尝试画图，完成表格：