初中数学人教版八年级上册12.2 三角形全等的判定评课ppt课件

这是一份初中数学人教版八年级上册12.2 三角形全等的判定评课ppt课件，共21页。PPT课件主要包含了△ABF≌△ACF，数学问题，ASA或AAS，SAS，几何语言，连接AB，AC＝BD，∠ADB＝∠CBD，AD∥BC，已知两边等内容，欢迎下载使用。
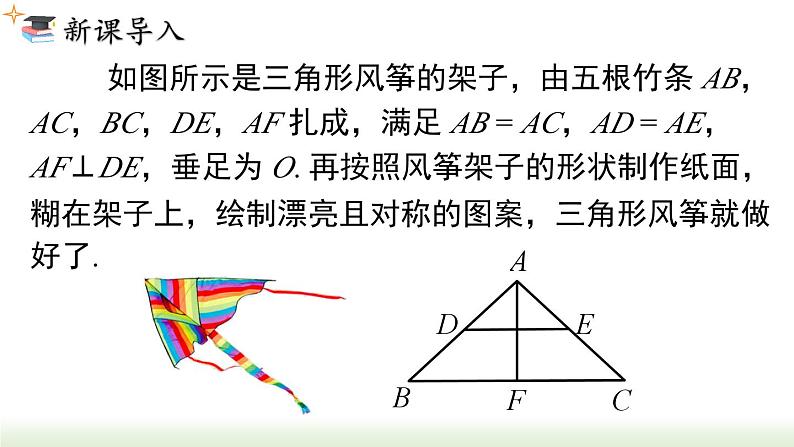
如图所示是三角形风筝的架子，由五根竹条 AB，AC，BC，DE，AF 扎成，满足 AB = AC，AD = AE，AF⊥DE，垂足为 O. 再按照风筝架子的形状制作纸面，糊在架子上，绘制漂亮且对称的图案，三角形风筝就做好了.
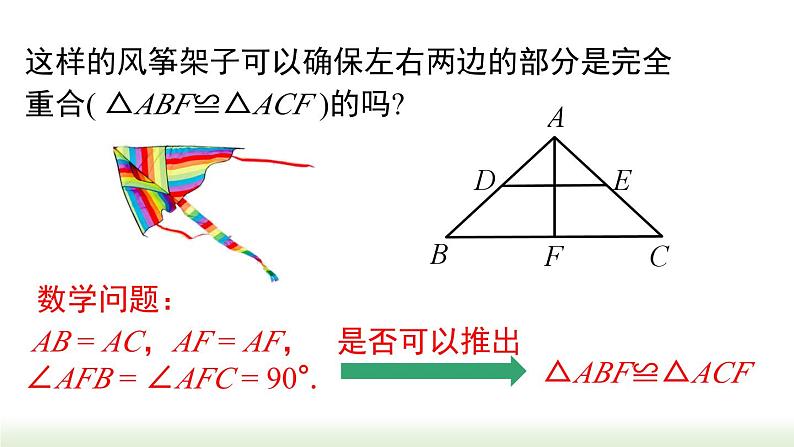
这样的风筝架子可以确保左右两边的部分是完全重合( △ABF≌△ACF )的吗?
AB = AC，AF = AF，∠AFB = ∠AFC = 90°.
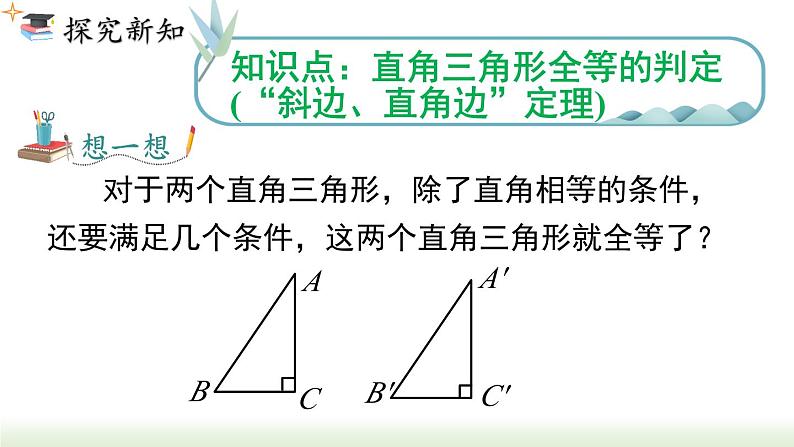
知识点：直角三角形全等的判定(“斜边、直角边”定理)
对于两个直角三角形，除了直角相等的条件，还要满足几个条件，这两个直角三角形就全等了？
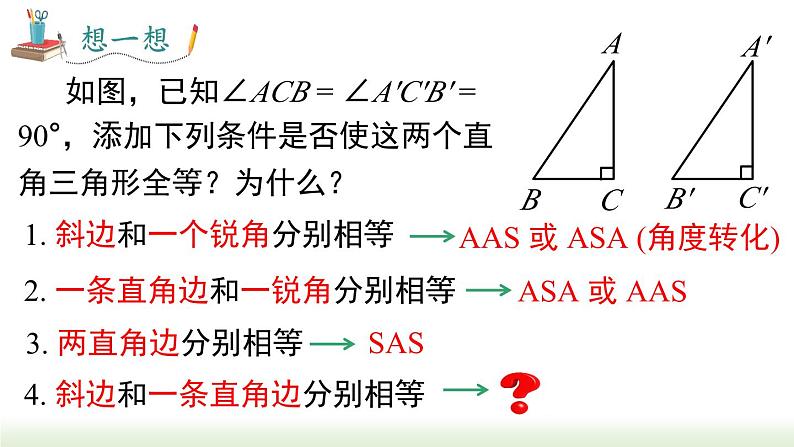
如图，已知∠ACB = ∠A′C′B′ = 90°，添加下列条件是否使这两个直角三角形全等？为什么？
1. 斜边和一个锐角分别相等
2. 一条直角边和一锐角分别相等
3. 两直角边分别相等
4. 斜边和一条直角边分别相等
AAS 或 ASA (角度转化)
任意画出一个 Rt△ABC，使∠C = 90°. 再画一个 Rt△A′B′C′ ，使∠C′ = 90°，B′C′ = BC，A′B′ = AB，把画好的 Rt△A′B′C′ 剪下来，放到 Rt△ABC 上，它们全等吗？
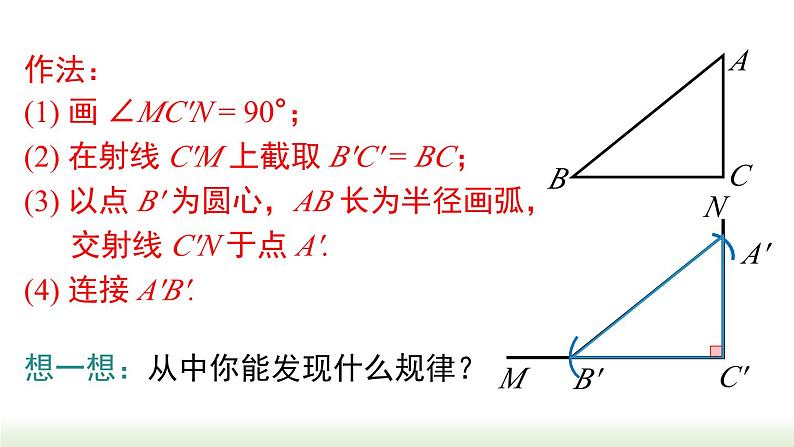
作法：(1) 画 ∠MC'N = 90°；(2) 在射线 C'M 上截取 B'C' = BC；(3) 以点 B' 为圆心，AB 长为半径画弧， 交射线 C'N 于点 A'. (4) 连接 A'B'.
想一想：从中你能发现什么规律？
文字语言：斜边和一条直角边分别相等的两个直角三角形全等(简写成“斜边、直角边”或“HL”).
在 Rt△ABC 和 Rt△A′B′C′ 中，
∴ Rt△ABC≌Rt△A′B′C′ (HL).
例1 如图，AC⊥BC，BD⊥AD，垂足分别为 C，D， AC = BD. 求证 BC = AD.
求证 BC = AD.
已知 AC⊥BC，BD⊥AD，AC = BD
求证 Rt△ABC≌Rt△BAD(HL).
证明：∵ AC⊥BC，BD⊥AD， ∴∠C 与∠D 都是直角.
在 Rt△ABC 和 Rt△BAD 中，
∴ Rt△ABC≌Rt△BAD (HL).∴ BC = AD.
变式1 如图，AC、BD 交于点 P，AC⊥BC，BD⊥AD，垂足分别为 C、D，AD = BC. 求证：AC = BD.
Rt△BAC≌Rt△ABD
变式2 如图，AB⊥AD，CD⊥BC，AB = CD，判断 AD 和 BC 的位置关系.
Rt△ABD≌Rt△CDB
梳理你所学的判定两个三角形全等的基本方法，并绘制成思维导图.
找两边的夹角“SAS”
看是否是直角三角形，若是“HL”
找两角的夹边“ASA”
找任意一角的对边“AAS”
找这条边的另外一个邻角“ASA”
找这个角的另外一边“SAS”
找这条边的对角“AAS”
找另外任意一个角“AAS”
看这个角是否是直角，若是，找任意一条直角边“HL”
1. (新余校考) 如图，CD⊥AB，BE⊥AC，垂足分别为 D、E，BE、CD 相交于点 O，如果 AB = AC，求证：AO 平分∠CAB.
证明：∵ CD⊥AB，BE⊥AC，∴∠ADC＝∠AEB＝90°.在△ACD 和△ABE 中， ∠ADC＝∠AEB， ∠DAC＝∠EAB， AC＝AB ，
∴△ACD≌△ABE (AAS). ∴ AD＝AE.在Rt△AOD 和Rt△AOE 中， OA＝OA， AD＝AE， Rt△AOD≌Rt△AOE(HL).∴ ∠DAO＝∠EAO.∴ AO 平分∠CAB.
__________________分别相等的两个直角三角形全等
在______三角形中
只须找除直角外的两个条件即可(两个条件中至少有一个是一对边相等)
1. 如图，有垂直于地面的两个木箱，高度分别为 AB = 5，DC = 10. 两个木箱之间恰好可以放进一个等腰直角三角板( AE = DE，∠AED = 90°)，点 B，C，E 在水平地面上，点 A 和点 D 分别与木箱的顶端重合，两个木箱之间的距离等于_______.
证明：∵ AD，AF 分别是钝角△ABC 和△ABE 的高，∴∠D＝∠F＝90°.在 Rt△ADC 和 Rt△AFE 中， AC＝AE， AD＝AF，∴ Rt△ADC≌Rt△AFE (HL). ∴ CD＝EF.在 Rt△ABD 和 Rt△ABF 中，
2. (集贤期中)如图，已知 AD，AF 分别是钝角△ACB 和△AEB 的高，如果 AD＝AF，AC＝AE，求证 BC＝BE.
∴ Rt△ABD≌Rt△ABF(HL).
∴ BD－CD＝BF－EF，即 BC＝BE.
3. 如图，有一直角三角形 ABC，∠C ＝ 90°，AC＝10 cm，BC＝5 cm，一条线段 PQ＝AB，P、Q 两点分别在 AC 上和过 A 点且垂直于 AC 的射线 AQ 上运动，问 P 点运动到 AC 上什么位置时△ABC 才能和△APQ 全等？
解：①当 P 运动到 AP＝CB 时，∵∠C＝∠QAP＝90°.在 Rt△ABC 与 Rt△QPA 中， PQ＝AB， AP＝BC，∴ Rt△ABC≌Rt△PQA (HL). ∴ AP＝BC＝5 cm；