初中数学第十三章 轴对称13.1 轴对称13.1.2 线段的垂直平分线的性质教学演示课件ppt

这是一份初中数学第十三章 轴对称13.1 轴对称13.1.2 线段的垂直平分线的性质教学演示课件ppt，共32页。PPT课件主要包含了学习目标，新课导入，复习引入，新知探究，验证猜想，跟踪训练，AFBF，ACAF+CF，ACBF+CF，APBP等内容，欢迎下载使用。
1.理解并掌握线段垂直平分线的性质和判定的内容.（重点）2.熟练运用线段垂直平分线的性质和判定进行计算与证明.（难点）3.会用尺规过直线外一点作已知直线的垂线.
1.什么是轴对称图形？
如果一个平面图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形，这条直线就是它的对称轴.这时，我们也说这个图形关于这条直线（成轴）对称.
2.线段是轴对称图形吗？它的对称轴是什么？
3.什么是线段的垂直平分线？
线段是轴对称图形，它的对称轴是这条线段的垂直平分线.
经过线段中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线.
经测量可以发现，点P1，P2，P3，…到点A的距离与它们到点B的距离分别 ，即
P1A ____P1B
P2A ____ P2B
P3A ____ P3B
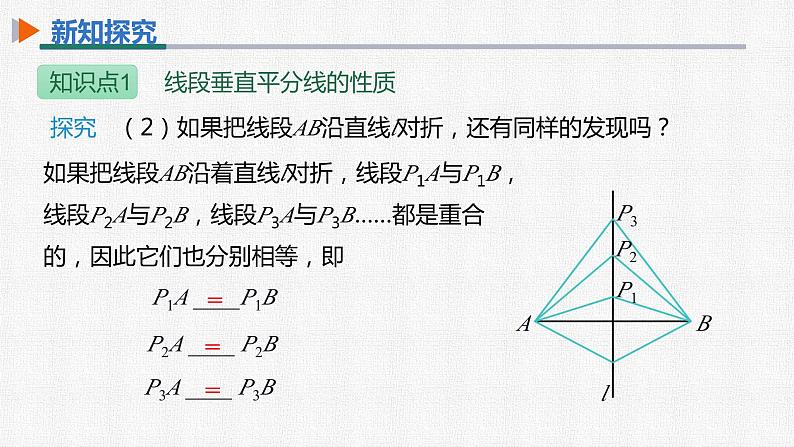
探究 （2）如果把线段AB沿直线l对折，还有同样的发现吗？
如果把线段AB沿着直线l对折，线段P1A与P1B，线段P2A与P2B，线段P3A与P3B……都是重合的，因此它们也分别相等，即
猜想 若一点在某线段的垂直平分线上，那么这点与这条线段两个端点的距离相等.
已知：如图，直线l⊥AB，垂足为C，AC=CB，点P在l上．求证：PA=PB．
证明：∵l⊥AB，∴∠PCA =∠PCB．又CA=CB，PC =PC，∴△PCA≌△PCB（SAS）．∴PA=PB．
该性质定理的几何语言：
∵直线l⊥AB，垂足为C，AC=BC，点P在l上，∴PA=PB.
如图，在△ABC中，ED垂直平分AB，交AB于点D ,交AC于点F，交BC的延长线于点E,若BF=6，CF=2，则AC的长为　 　.
【解析】ED垂直平分AB
已知：如图，P是线段AB外一点，且PA=PB．求证：点P在线段AB 的垂直平分线上．
证明：如图，过点P 作PC⊥AB 于点C，则∠PCA =∠PCB =90°．
∴Rt△PCA≌Rt△PCB（HL）．∴AC=BC．又PC⊥AB，∴点P 在线段AB 的垂直平分线上．
该判定定理的几何语言：
∵PA=PB，∴点P在线段AB的垂直平分线上.
例1 如图,在ΔABC中,边AB的垂直平分线EF交BC的垂直平分线MN于点P，连接AP，BP，CP.求证：AP=BP=CP.
EF是线段AB的垂直平分线，点P在EF上
MN是线段BC的垂直平分线，点P在EF上
证明：∵点P在线段AB的垂直平分线MN上，∴AP=BP.同理 BP=CP.∴AP=BP=CP.
例2 如图,在ΔABC中,边AB的垂直平分线EF交BC的垂直平分线MN于点P.求证：点P在AC的垂直平分线上.
证明：连接AP，BP，CP.∵AB的垂直平分线EF交BC的垂直平分线MN于点P，∴PA=PB, PB=PC.∴PA=PC.∴点P在AC的垂直平分线上.
例3 尺规作图：经过已知直线外一点作这条直线的垂线.
已知：直线AB和AB外一点C(如图） .
求作：AB的垂线，使它经过点C .
作法：（1）任意取一点K，使点K和点C在AB的两旁.
（2）以点C 为圆心，CK长为半径作弧，交AB于点D和点E.
直线CF就是所求作的垂线.
为什么直线CF就是所求作的垂线？
因为DF=EF，根据垂直平分线的判定定理即可得到.
线段的垂直平分线的性质与判定
线段垂直平分线上的点与这条线段两个端点的距离相等
判断一个点是否在线段的垂直平分线上
与线段两个端点距离相等的点在这条线段的垂直平分线上
1.如图，直线CD是线段AB的垂直平分线，点P为直线CD上的一点，且PA=5，AD=3，PD=4，则线段PB的长为（ ）A. 6 B. 5 C. 4 D. 3
2.（2021•梧州）如图，DE是△ABC的边BC的垂直平分线，分别交边AB，BC于点D，E，且AB＝9，AC＝6，则△ACD的周长是（　　）A．10.5 B．12 C．15 D．18
【解析】∵DE是△ABC的边BC的垂直平分线，∴BD＝CD，∴△ACD的周长＝AD+CD+AC＝AD+BD+AC＝AB+AC，∵AB＝9，AC＝6，∴△ACD的周长＝9+6＝15．故选C．
3.如图，在四边形ADBC中，AB与CD互相垂直平分，垂足为点O.则图中相等的线段有 .
OC=OD，AO=OB，且AC=BC=AD=BD
4.如图，在Rt△ABC中，∠C=90°, BD平分∠ABC，交AC于点D，DE垂直平分AB交AB于点E，若DE=1 ,BD=2，则AC= .
【解析】∵DE垂直平分AB，BD=2,∴AD=BD=2.∵BD平分∠ABC，∠C=90°，DE⊥AB，∴CD=DE=1，∴AC=AD+CD=2+1=3.故答案为3.
【变式】（2021•杭州二模）如图，在△ABC中，∠C＝90°，E是AC上的点，且∠1＝∠2，DE垂直平分AB，垂足是D，S△AED：S△ABC＝ ．
【解析】∵DE垂直平分AB，∴AD=BD，∴S△AED=S△BED.∵∠C=∠BDE=90°，∠1=∠2，BE=BE，∴△BDE≌△BCE（AAS）.∴S△BED=S△BEC，∴S△ABC=3S△AED，∴S△AED：S△ABC=1：3．故答案为1：3．
5.如图，点E是∠AOB的平分线上一点，EC⊥OA,ED⊥OB,垂足分别为C,D，连接CD.求证：OE是CD的垂直平分线.
∵OE平分∠AOB,EC⊥OA,ED⊥OB,∴DE=CE.
又OE=OE，∴Rt△OED≌Rt△OEC.
∴DO=CO.∴OE是CD的垂直平分线.
6.如图，AD⊥BC，BD=DC，点C在AE的垂直平分线上，求证：AB+BD=DE.
证明：∵AD⊥BC，BD=DC， ∴AB=AC.∵点C在AE的垂直平分线上, ∴AC=CE.∴AB=AC=CE.∴AB+BD=CE+DC=DE，即AB+BD=DE.
7.如图，四边形ABCD中，AB=AD，BC=DC，E是AC上的一点，连接DE，BE，求证：∠ABE=∠ADE.
证明：连接DB.∵AB=AD，BC=DC,∴点A和点C都在线段BD的垂直平分线上. ∴线段AC所在的直线是线段BD的垂直平分线.∵E是AC上的一点，∴BE=DE.
8.如图，在△ABC中，AD平分∠BAC，AE=AF,请判断线段AD所在的直线是否为线段EF的垂直平分线.如果是，请予以证明；如果不是，请说明理由．
解：线段AD所在的直线是线段EF的垂直平分线.证明如下：
方法一（定义法）：设AD与EF的交点为O.
∵AD平分∠BAC，∴∠EAD=∠FAD，又AE=AF，AO=AO，∴△AOE≌△AOF（SAS）.
∴EO=FO，∠EOA=∠FOA.又∠EOA+∠FOA=180°.∴∠EOA=∠FOA=90°，即AO⊥EF.∴线段AD所在的直线是线段EF的垂直平分线.