初中数学北师大版八年级上册1 探索勾股定理导学案

第一章   勾股定理导学案

第1课时  探索勾股定理

学习目标：

1、经历探索勾股定理的过程。

  2、利用拼图及列式变形等方法验证勾股定理。

学习过程：

一、课前预习：

1、三角形按角的大小可分为：            、           、          。

2、直角三角形的两个锐角           ；

3、三角形的三边关系：

 三角形的任意两边之和            ；任意两边之差              。

4、在RtΔABC中，两条直角边长分别为a、b，则 这个直角三角形的面积可以表示为：               。 

二、自主学习：    探索直角三角形三边的特殊关系： 

1、       （1）直角三角形的两条直角边的长度分别为a=3㎝，b=4㎝，请你量出斜边c的长度。

（2）画出一个直角三角形，两条直角边分别为a=6cm和b=8cm，并量出斜边的长度。                   

（3）请任意画出一个直角三角形，两条直角边长度为整数，测量斜边的长度。

2、进行有关的计算：(1)a2+b2=          c2=         (2) a2+b2=         c2=

(3) a2+b2=         c2=

3、猜想直角三角形三边的关系：

三、合作探究：

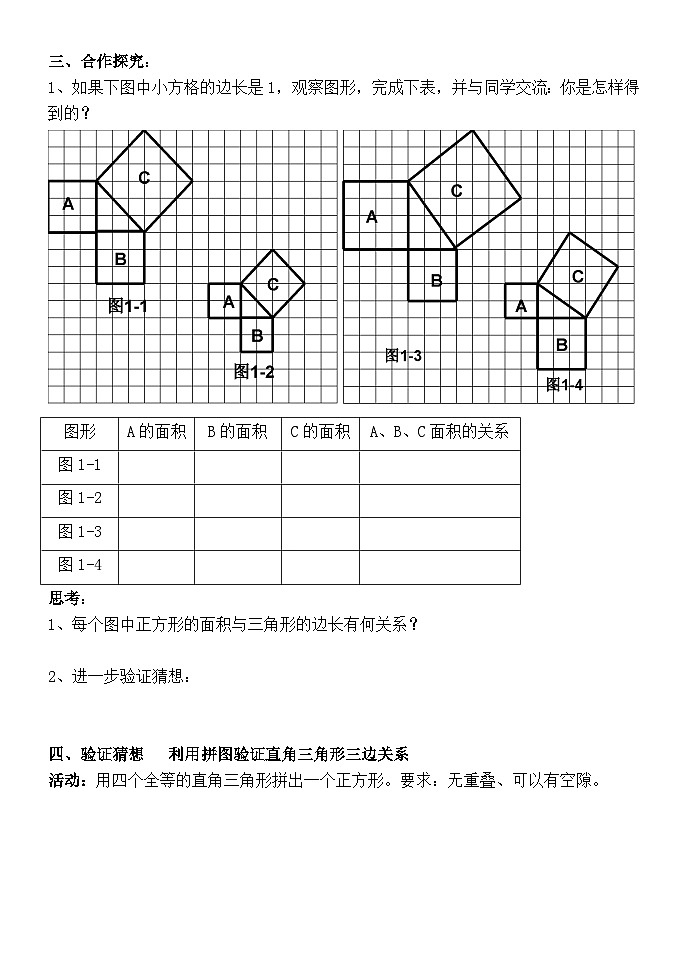
1、如果下图中小方格的边长是1，观察图形，完成下表，并与同学交流：你是怎样得到的？

思考：

1、每个图中正方形的面积与三角形的边长有何关系？

2、进一步验证猜想：

四、验证猜想   利用拼图验证直角三角形三边关系

活动：用四个全等的直角三角形拼出一个正方形。要求：无重叠、可以有空隙。

勾股定理：

直角三角形                              等于             ；       

几何语言表述：如图1.1-1，在RtΔABC中，C＝ 90°，

则：                     

五、课堂小结：

1、通过本节课的学习，你觉得我们是如何对直角三角形进行研究的呢？

1、本节课你学习到了哪些数学思想方法？

六、课堂检测：

1、求下列直角三角形的未知边的长

2、如果直角三角形的两边长分别为3和4,那么第三边的平方是         。

3、在直角三角形ABC中，斜边AB=2，则AB²+BC²+AC²=         。

4、在△ABC中，∠C=90°，BC=3，AC=4，以斜边AB为直径做半圆，则这个半圆的面积是        。

作业：

1、查阅相关资料，了解勾股定理。

2、证明勾股定理的方法有很多种，你能有其他的证明方法吗？

3、观察下图,用数格子的方法判断图中三角形的三边长的关系。

左图：a2+b2      c2                       右图：a2+b2      c2

由此，你得出什么结论？