高中数学苏教版 (2019)选择性必修第一册4.1 数列习题

这是一份高中数学苏教版 (2019)选择性必修第一册4.1 数列习题，共7页。试卷主要包含了 在数列中,,,则， 已知数列的前项和满足， 已知的前项和为,,当时,,则， 在数列中,,,且,则等内容，欢迎下载使用。
A层 基础达标练
1. 已知数列,满足,,则的前10项和为( )
A. B. C. D.
2. 设函数,利用课本中推导等差数列前项和的方法，求得的值为( )
A. 9B. 11C. D.
3. （多选题）设等差数列满足,,公差为,则下列说法正确的是( )
A. B.
C. D. 的前 项和为
4. 在数列中,,,则.
5. 已知数列的前项和为,且满足,则数列的前项和.
6. 已知数列的前项和满足.
（1） 求数列的通项公式；
（2） 令，求数列的前项和.
B层 能力提升练
7. 已知的前项和为,,当时,,则( )
A. 1 008B. 1 009C. 1 010D. 1 011
8. 列昂那多·斐波那契（意大利著名数学家）以兔子繁殖为例,引入“兔子数列”,1,2,3,5,8,13,21,34,55,,即,,,此数列在现代物理、化学等学科都有着十分广泛的应用.若此数列的各项除以2后的余数构成一个新数列,设数列的前项和为,若数列满足,设数列的前项和为,则( )
A. 1 349B. 1 348C. 674D. 673
9. 设数列满足，，则数列的前19项和为( )
A. B. C. D.
10. 在数列中,,,且,则.
11. 已知数列的各项均为正数，，，则数列的前10项和为.
12. 数学中有许多猜想，如法国数学家费马于1640年提出了以下猜想：是质数.直到1732年才被善于计算的大数学家欧拉算出不是质数.现设，，则数列{}的前21项和为.
13. 设集合,2,3,,,对的任意非空子集,定义为中的最大元素,当取遍的所有非空子集时,对应的的和为,则.
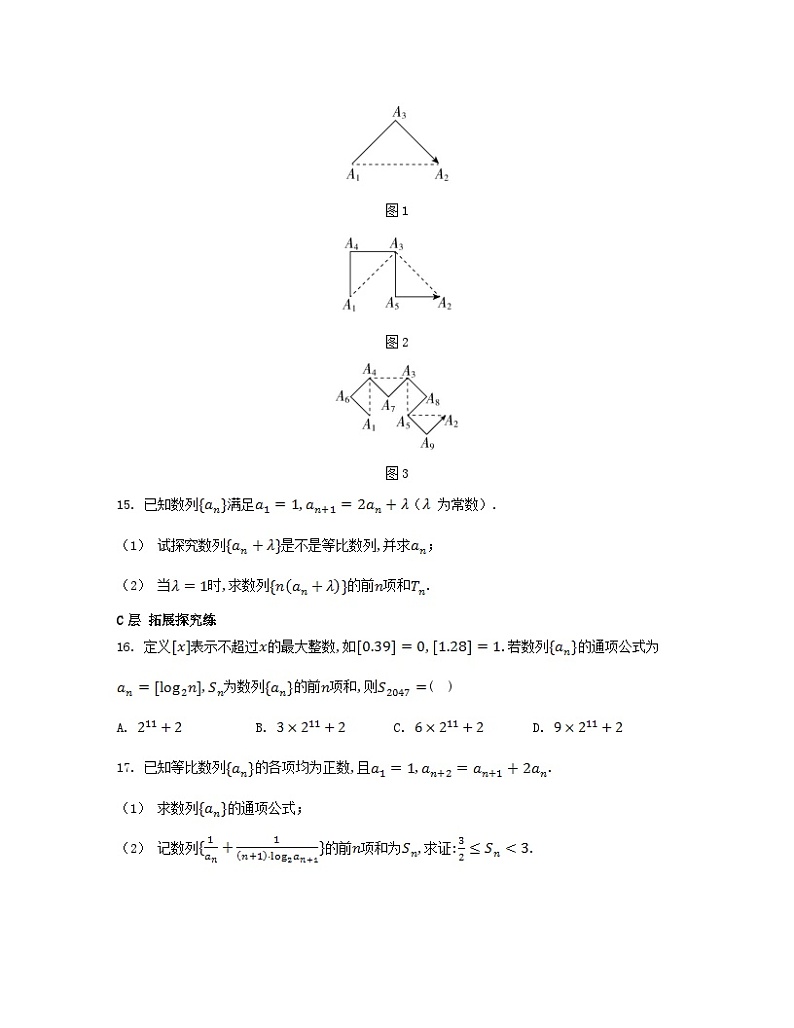
14. 龙曲线是由一条单位线段开始，按下面的规则画成的图形：将前一代的每一条折线段都作为这一代的等腰直角三角形的斜边，依次画出所有直角三角形的两段，使得所画的相邻两线段永远垂直（即所画的直角三角形在前一代曲线的左右两边交替出现）.例如，第一代龙曲线（图1）是以为斜边画出等腰直角三角形的直角边，所得的折线图，图2、图3依次为第二代、第三代龙曲线（虚线即为前一代龙曲线），，为第一代龙曲线的顶点，设第代龙曲线的顶点数为，由图可知，，，则；数列的前项和.
图1
图2
图3
15. 已知数列满足,（ 为常数）.
（1） 试探究数列是不是等比数列,并求；
（2） 当时,求数列的前项和.
C层 拓展探究练
16. 定义表示不超过的最大整数,如,.若数列的通项公式为,为数列的前项和,则( )
A. B. C. D.
17. 已知等比数列的各项均为正数,且,.
（1） 求数列的通项公式；
（2） 记数列的前项和为,求证:.
培优课 数列求和
分层作业
A层 基础达标练
1. D
2. B
3. ABD
4.
5. （）
6. （1） 解 当时，，故.因为，所以当时，,两式相减得，即，故数列为等比数列，公比为2，
所以.
（2） ，故，故.令，则，，得，即，故.
B层 能力提升练
7. D
8. B
9. D
[解析]因为，所以,,,，所以.又，所以，则
，故数列的前19项和为.故选.
10. 676
11.
[解析]由或，当，即时，数列是以为公比的等比数列，这与数列的各项均为正数不相符；当，即时，数列是以2为公比的等比数列，又，所以.因为，所以的前10项和为.
12.
13. 129
[解析]由,2,3,,,知的任意非空子集共有个,其中最大值为的有个,最大值为的有个,,最大值为1的有个,
故,
所以,
两式相减，得,
所以,
故,
所以.
14. 17;
[解析]由题意，得,,，由,,,，，易知，所以，所以.
15. （1） 解 因为 ,所以.
又,所以当时,,数列不是等比数列,此时,即；
当时,,所以,所以数列是以 为首项,2为公比的等比数列,此时,即 .
（2） 当时，,所以,
,①
,②
，得，所以.
C层 拓展探究练
16. D
[解析]因为,所以.
当时,,即（共1项）；
当时,,3,即（共2项）；
当时,,5,6,7,
即（共4项）；
……
当时,,,,,即（共项）.
由,得,
即,所以，
所以,
则,
两式相减，得,
所以.故选.
17. （1） 解 设等比数列的公比为.
因为,所以,解得,所以.
（2） 证明 因为,所以.
因为对,有,,
所以,即.