福建省龙岩市第七中学2022-2023学年八年级下学期期中数学试题(无答案)

2022-2023学年第二学期期中质量监测

八年级数学试卷

出卷人：葛秀康    审核人：刘秀平

（时间：120分钟    满分：150分）

一、单选题（本大题共10个小题，每小题4分，满分40分，每小题均有四个选项，其中只有一项符合题目要求）

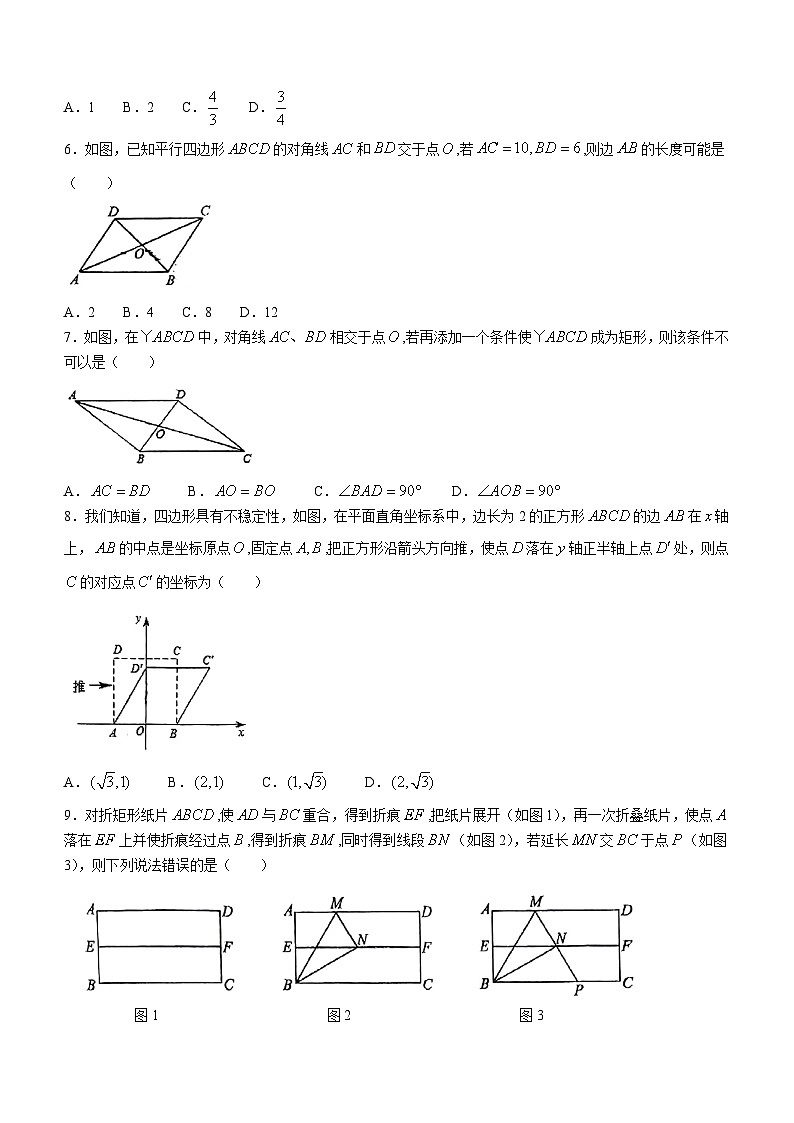
1．若在实数范围内有意义，则的取值范围（    ）

A．     B．    C．     D．

2．下列二次根式中，属于最简二次根式的是（    ）

A．    B．     C．    D．

3．在中，的对边分别是，下列条件中，不能判定是直角三角形的是（    ）

A．        B．

C．    D．

4．下列图象中，表示是的函数的是（    ）

A．                     B．

C．                     D．

5．如图，中，,点分别是边的中点，点在线段上，且,则的长为（    ）

A．1    B．2    C．    D．

6．如图，已知平行四边形的对角线和交于点,若,则边的长度可能是（    ）

A．2    B．4    C．8    D．12

7．如图，在中，对角线相交于点,若再添加一个条件使成为矩形，则该条件不可以是（    ）

A．     B．     C．    D．

8．我们知道，四边形具有不稳定性，如图，在平面直角坐标系中，边长为2的正方形的边在轴上，的中点是坐标原点,固定点,把正方形沿箭头方向推，使点落在轴正半轴上点处，则点的对应点的坐标为（    ）

A．     B．     C．     D．

9．对折矩形纸片,使与重合，得到折痕,把纸片展开（如图1），再一次折叠纸片，使点落在上并使折痕经过点,得到折痕,同时得到线段（如图2），若延长交于点（如图3），则下列说法错误的是（    ）

          图1                        图2                        图3

A．     B．    C．是等边三角形    D．点为的中点

10．数学教有家波利亚曾说：“对一个数学问题，改变它的形式，变换它的结构，直到发现有价值的东西，这是数学解题的一个重要原则”．在复习二次根式时，老师提出了一个求代数式最小值的问题，如：“当时，求代数式的最小值”，其中可看作两直角边分别为和2的的斜边长，可看作两直角边分别是和3的的斜边长．于是构造出如图，将问题转化为求的最小值，运用此方法，请你解决问题：己知均为正数，且．则的最小值是（    ）

A．     B．8    C．10    D．34

二、填空题（共6小题，每小题4分，满分24分）

11．直角三角形中，若两条直角边的长分别为3,5，则第三条边的长为________．

12．已知实数在数轴上的位置如图所示，则化简代数式的结果________

13．用的铁丝围成长为、宽为的长方形，当时，________．

14．如图，点所表示的数是________

15．如图，中，，，平分,如果点,点分别为上的动点，那么的最小值是________．

16．如图，中，对角线相交于分别是的中点．下列结论①；②四边形是平行四边形；③;④平分．其中正确的是________．

三、解答题（共9小题，满分86分）

17．（8分）计算：（1）

（2）．

18．（8分）如图反映的是小华从家里跑步去体育馆，在那里锻炼了一段时间后又走到文具店去买笔，然后散步回家，其中（分）表示时间，（千米）表示小华离家的距离．根据图像回答下列问题：

（1）体育馆距离小华家________千米，小华在体育馆锻炼了________分钟；

（2）体育馆距离文具店________千米，小华在文具店买笔用了________分钟；

（3）小华从家跑步到体育馆，从文具店散步回家的速度分别是多少千米/分钟？

19．（8分）如图，在中，,求证：．

20．（8分）如图，数学兴趣小组要测量旗杆的高度，同学们发现系在旗杆顶端的绳子垂到地面并多出一段（如图1），聪明的小迪发现：先测出绳子多出的部分长度为米，再将绳子拉直（如图2），测出绳子末端到旗杆底部的距离米，利用所学知识就能求出旗杆的长，若．求旗杆的长．

        图1                 图2

21．（8分）如图，己知,点在上，点在上．

（1）请用尺规确定点的位置，使得四边形是菱形；（保留作图痕迹，不写作法）

（2）利用（1）中作图所确定的条件证明四边形是菱形．

22．（10分）如图在的正方形网格中，若小正方形的边长为1，的顶点在网格的格点上．

       图1                      图2

（1）图1中的周长为__________________．（结果保留根号）

（2）若点的坐标为，请你在图中找出一点,使四个点为顶点的四边形为平行四边形，则满足条件的点坐标是______________________

（3）在图2中画出以为一边长，另外两边长分别为和的格点．

23．（10分）已知，矩形中，是边上的一个动点，点分别是的中点．

（1）求证：．

（2）若,当四边形是正方形时，求矩形的面积．

24．（12分）阅读材料：小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如，善于思考的小明进行了以下探索：

若设（其中均为整数），则有．这样小明就找到了一种把类似的式子化为平方式的方法，请你仿照小明的方法探索并解决下列问题：

（1）若,当均为整数时，用含的式子分别表示,得：________,________；

（2）若,且均为正整数，求的值；

（3）化简：

25．（14分）如图1，正方形的边长为,点从点出发，沿射线方向以/秒的速度移动，点从点出发，向点以/秒的速度移动（不到点）．设点同时出发移动秒．

       图1                  图2                    图3

（1）在点移动过程中，连接，请判断的形状并说明理由；

（2）如图2，连接，设交于点，当时，求的长；

（3）如图3，点分别在边上，且,连接,当与的夹角为，求的值．