《“斜边、直角边”判定直角三角形全等》教学设计1-八年级上册数学人教版

12.2（5）“斜边、直角边”判定直角三角形全等  

一、内容和内容解析

1．内容

构建两个直角三角形全等条件的探索思路，HL判定方法。

2.内容解析

由于直角是特殊的三角形它还具备一般三角形所没有的特殊性质。例如，对一般三角形来说，已知两边和其中一边的对角对应相等的两个三角形不一定全等!而对于直角三角形来说，已知斜边和一条直角边分别相等，能够得到两个直角三角形全等的结论。由于没学勾股定理和等腰三角形性质，无法证明，与前面判定方法的处理方式类似，我用几何画板先直观演示，让学生猜想三角形形状，然后安排画图实验，通过画一直角边和斜边分别相等的两直角三角形并进行比较，得出HL判定方法。

基于以上分析，确定本节课的教学重点：构建两个直角三角形全等条件的探索思路，HL判定方法。

二、目标和目标解析

1.目标

（1）构建直角三角形全等条件的探索思路，体会研究几何问题的方法。

（2）探索并掌握两个直角三角形全等的条件：HL，并能应用它判别两个直角三角形是否全等．

（3）会用尺规作一个直角三角形全等已知三角形，了解作图的道理。

2.目标解析

达成目标（1）的标志是：知道一般三角形已知两边和其中一边的对角对应相等的两个三角形不一定全等，但直角三角形已知两边和其中一边的对角对应相等的两个三角形一定全等，这是因为边所对的角的大小决定了三角形的形状，大于或等于90度时两三角形一定全等。提高分析、作图、归纳、表达、逻辑推理等能力；并通过对知识方法的总结，培养反思的习惯，培养理性思维．

达成目标（2）的标志是：学生能在老师引导下，经历观察、比较、猜想、作图等探究过程，探索并掌握两个直角三角形全等的条件：HL，会用HL判定方法进行证明。

达成目标（3）的标志是：学生明确尺规作图的基本要求，知道用尺规作直角三角形一条直角边和斜边与已知三角形对应直角边和斜边相等的方法与原理，能在教师引导下完成。

三、教学问题诊断分析

探索两个直角三角形全等的条件：HL，是一个特殊情况，以前一般三角形已知两边和其中一边的对角对应相等的两个三角形不一定全等，是因为所对的角是锐角，可以画出反例，有一个锐角三角形和一个钝角三角形或两个钝角三角形两种情况。教学时可以用软件演示，让学生观察所对角的变化，猜想角的取值范围。由于没有学勾股定理和等腰三角形性质，证明只能取特殊值90度通过作图，剪裁，叠合来验证HL。

四、教学过程设计

1.复习全等判定方法，直角三角形全等条件添加

问题1：复习（1）判定两个三角形全等方法有：     ，     ，       ，       。

师生活动：教师提问，学生回答，教师逐一展示结论。

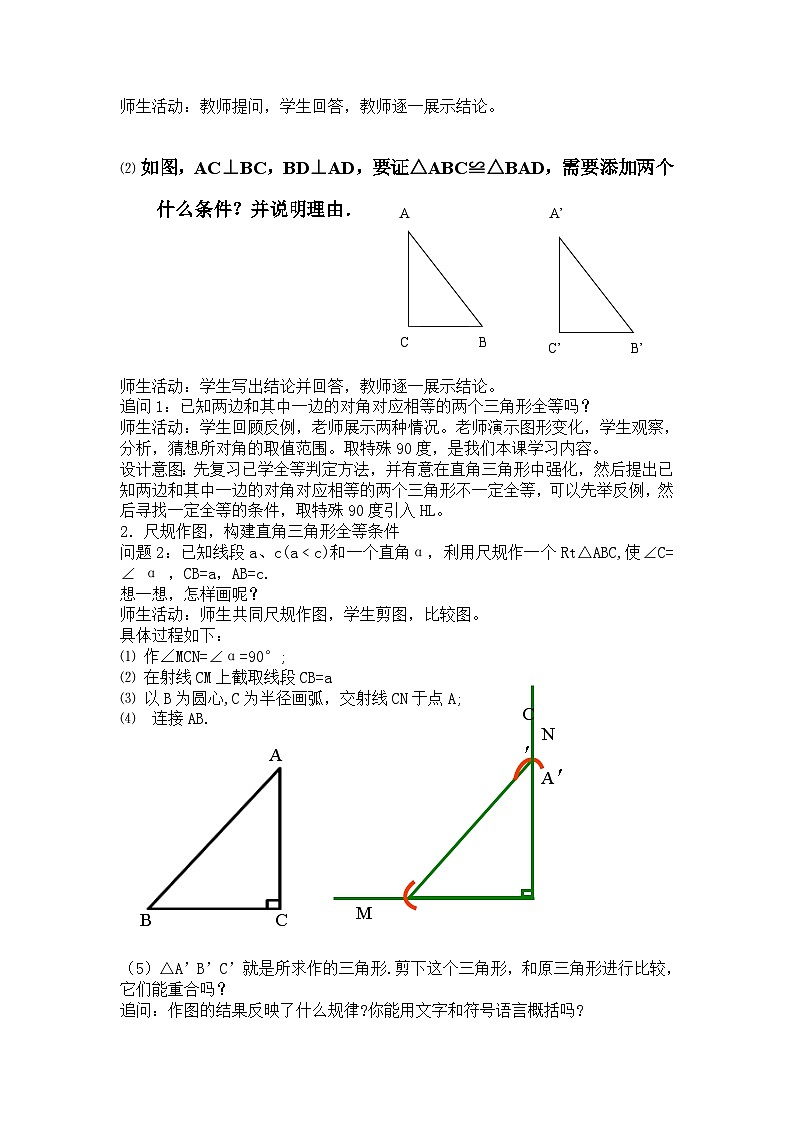
⑵ 如图，AC⊥BC，BD⊥AD，要证△ABC≌△BAD，需要添加两个什么条件？并说明理由．

师生活动：学生写出结论并回答，教师逐一展示结论。

追问1：已知两边和其中一边的对角对应相等的两个三角形全等吗？

师生活动：学生回顾反例，老师展示两种情况。老师演示图形变化，学生观察，分析，猜想所对角的取值范围。取特殊90度，是我们本课学习内容。

设计意图：先复习已学全等判定方法，并有意在直角三角形中强化，然后提出已知两边和其中一边的对角对应相等的两个三角形不一定全等，可以先举反例，然后寻找一定全等的条件，取特殊90度引入HL。

2．尺规作图，构建直角三角形全等条件

问题2：已知线段a、c(a﹤c)和一个直角α，利用尺规作一个Rt△ABC,使∠C= ∠ α ，CB=a，AB=c.

想一想，怎样画呢？

师生活动：师生共同尺规作图，学生剪图，比较图。

具体过程如下：

⑴ 作∠MCN=∠α=90°;

⑵ 在射线CM上截取线段CB=a

⑶ 以B为圆心,C为半径画弧，交射线CN于点A;

⑷    连接AB.

（5）△A’B’C’就是所求作的三角形.剪下这个三角形，和原三角形进行比较，它们能重合吗？

追问：作图的结果反映了什么规律?你能用文字和符号语言概括吗?

文字:斜边和一条直角边对应相等的两个直角三角形全等.(简写成“斜边、直角边”或“HL”.)

符号:

在Rt△ABC和Rt△A’B’C’中,

BC=B’C’,

          AB=A’B’,

∴ Rt△ABC≌Rt△A’B’C’ (HL).

设计意图:通过作图、剪图、比较图的过程，感悟猜想的正确性，获得HL的判定方法，在叙述文字和符号语言的过程中，引导学生抓住问题的条件，锻炼学生用数学语言概括结论的能力。

3.运用HL判定方法，解决问题

例5　如图，AC⊥BC，BD⊥AD，AC =BD．求证：BC =AD．

证明：∵　AC⊥BC，BD⊥AD，

∴　∠C 和∠D 都是直角．

在Rt△ABC 和 Rt△BAD 中，

   AB =BA，

   AC =BD，

∴　Rt△ABC ≌ Rt△BAD（HL）．

∴　BC =AD（全等三角形对应边相等）．

师生活动：师生共同分析解题思路，找到隐含条件———公共边AB。学生口述证明过程，教师板书。

练习1 如图，AC⊥BC， DF⊥DE，AC =FD,

AE=FB.

求证：BC =ED．

师生活动： 学生独立完成，教师巡视，辅导，展示，学生修改。

练习2 如图，C 是路段AB 的中点，两人

从C 同时出发，以相同的速度分别沿两条直

线行走，并同时到达D，E 两地．DA⊥AB，

EB⊥AB． D，E 与路段AB的距离相等吗？

为什么？

师生活动：师生共同分析解题思路，找出题中已知条件。

设计意图: 直接找出直角边和斜边，间接找出相等的直角边，从实际问题中抽象直角三角形，运用“HL”，逐步增加问题的难度，考察学生能否抓住直角边与斜边这两个条件。

4.小结

教师与学生一起回顾本节课所学内容，并请学生回答以下问题：

（1）想一想这节课你有什么收获呢？与你的同伴进行交流。

（2）你能够用几种方法说明两个直角三角形全等？

直角三角形是特殊的三角形，所以不仅有一般三角形判定全等的方法:SAS、ASA、AAS、SSS，还有特殊的判定方法—“HL”.

设计意图:通过小结，使学生梳理本节课所学内容，掌握“HL”是直角三角形新增的判定方法。

5.布置作业：教科书习题12.2第6、7、8题．

五、目标检测设计

1 如图，两根长度为12米的绳子，一端系在旗杆上，

另一端分别固定在地面两个木桩上，两个木桩离旗

杆底部的距离相等吗？请说明你的理由。

设计意图:从实际问题中抽象直角三角形，直接找出直角边和斜边，运用“HL”.

2　如图，AB =CD，AE⊥BC，DF⊥BC，

垂足分别为E ，F，CE =BF．求证：AE =DF．

设计意图:间接找出相等的直角边。

3.如图，有两个长度相同的滑梯，左边滑梯的高度AC

与右边滑梯水平方向的长度DF相等，两个滑梯的倾

斜角∠ABC和∠DFE的大小有什么关系？

解：∠ABC+∠DFE=90°.理由如下：

在Rt△ABC和Rt△DEF中,

则

BC=EF,

   AC=DF .

∴ Rt△ABC≌Rt△DEF (HL).

∴∠ABC=∠DEF

(全等三角形对应角相等).

又 ∠DEF+∠DFE=90°,

∴∠ABC+∠DFE=90°.

设计意图:“HL”与同角的余角相等综合运用。