初中数学人教版八年级上册12.1 全等三角形教案

这是一份初中数学人教版八年级上册12.1 全等三角形教案，共5页。


教学目标
1通过对全等三角形的摆放,复习了全等三角形的判定和性质，等腰三角形的判定和性质，平行四边形的判定。
2.总结了证明线段和角相等的一些方法。
3.激发学生学习数学的兴趣,培养数学解题能力.
教学难点
通过对全等三角形的摆放,复习全等三角形的判定和性质，等腰三角形的判定和性质，平行四边形的判定,所涉及知识点多,要引导学生自主复习.
知识重点
全等三角形的判定和性质，等腰三角形的判定和性质，平行四边形的判定的应用
教学过程（师生活动）
情境导入
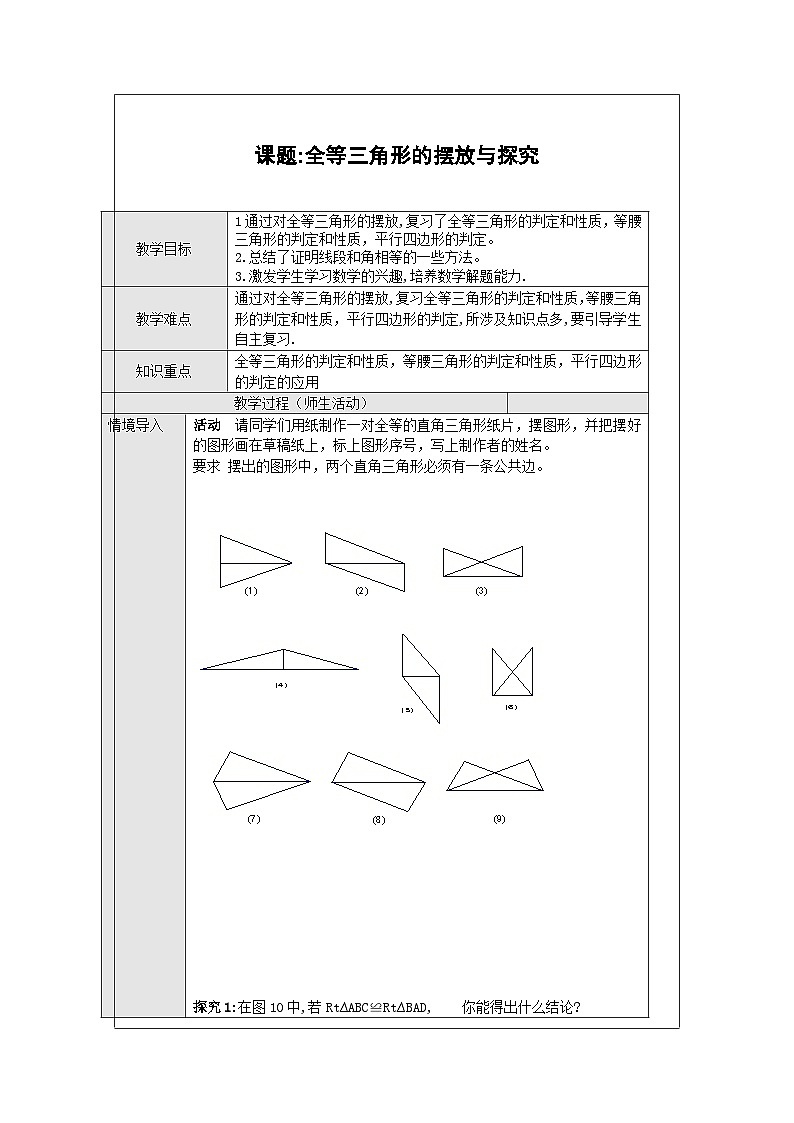
活动 请同学们用纸制作一对全等的直角三角形纸片，摆图形，并把摆好的图形画在草稿纸上，标上图形序号，写上制作者的姓名。
要求 摆出的图形中，两个直角三角形必须有一条公共边。
探究1:在图10中,若Rt∆ABC≌Rt∆BAD, 你能得出什么结论?
你能根据图形自己编一道题吗?(自己提出问题,自己写出解答的过程)
探究2
在图10中，若 Rt∆ABC ≌ ∆BAD ，延长AC、BD交于点M,(如图11)，你还能在图11中找到哪几对全等的三角形？为什么？你能判定△ABM的形状吗？
深入探究
问题1：已知在∆MAB中,AD,BC是高，且AD=BC,求证：MA=MB
把问题1中的条件和结论交换得到
问题2：
已知在∆MAB中,AD,BC是高，且MA=MB,
求证：AD=BC(请同学们证明问题3的真假）
通过验证问题2，你能总结出等腰三角形的什么性质？
(等腰三角形两腰上的高相等)
你对等腰三角形还能做什么猜想？
问题3：已知在∆MAB中,AD,BC是中线，
且MA=MB,求证：AD=BC
(等腰三角形两腰上的中线相等)
问题4：已知在∆MAB中,AD,BC是两底角平分线，且MA=MB,求证：AD=BC
(等腰三角形两底角的角平分线相等)
探究3:
如图，在∆ABC中，AB=AC,点D是BC的中点，
DEAB,DFAC,
垂足分别为E,F 求证：DE=DF

变式1
如图，在∆ABC中，AB=AC,点D是BC的中点，
DEAB,DFAC, CMAB
垂足分别为E,F ,M.试猜想线段DE,DF,CM
有何数量关系？并说明理由。

变式2
如图，在∆ABC中，AB=AC,点D是BC边上任意的一点，DEAB,DFAC, CMAB
垂足分别为E,F ,M.变式1中的结论是否仍然成立？若成立，给出证明；若不成立，直接写出新的数量关系。

变式3
如图，在∆ABC中，AB=AC,点D是BC延长线上任意的一点DEAB,DFAC, CMAB，垂足分别为E,F ,M.变式1中的结论是否仍然成立？若成立，给出证明；若不成立，直接写出新的数量关系

探究4
一对全等的三角形如图摆放，你能得到什么结论？能否说明理由。

小结
1.通过对一对全等三角形的摆放，复习了全等三角形的判定和性质，等腰三角形的判定和性质，平行四边形的判定。
2.总结了证明线段和角相等的一些方法。
3.有关垂直线段的数量关系问题可用面积法。
布置作业
创新探究
1.用一副（含30˚和45˚）直角三角板如图摆放，通过观察，分析，你能发现什么问题？得出什么结论？
2.你能在图中改变一个条件，提出一个更有研究价值的问题吗？
课后反思