人教版八年级上册13.1.2 线段的垂直平分线的性质课时练习

　13.1.2　线段的垂直平分线的性质

　　　　　　　　　　 必备知识·基础练

(打“√”或“×”)

1．线段垂直平分线上的点与这条线段两个端点的距离相等. (√)

2．与线段两个端点距离相等的点，在这条线段的垂直平分线上. (√)

3．若P为线段AB的垂直平分线CD上的一点，则PC＝PD. (×)

知识点1　线段的垂直平分线的性质

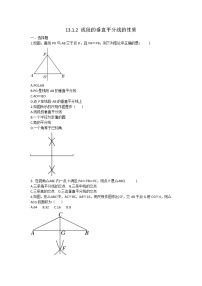
1．(2020·枣庄中考)如图，在△ABC中，AB的垂直平分线交AB于点D，交BC于点E，连接AE.若BC＝6，AC＝5，则△ACE的周长为(　B　)

A．8    B．11    C．16    D．17

【解析】∵DE垂直平分AB，

∴AE＝BE，

∴△ACE的周长＝AC＋CE＋AE＝AC＋CE＋BE

＝AC＋BC＝5＋6＝11.

2.(2020·益阳中考)如图，在△ABC中，AC的垂直平分线交AB于点D，DC平分∠ACB，若∠A＝50°，则∠B的度数为(　B　)

A.25°    B．30°    C．35°    D．40°

【解析】∵DE垂直平分AC，

∴AD＝CD，

∴∠A＝∠ACD，

又∵CD平分∠ACB，

∴∠ACB＝2∠ACD＝100°，

∴∠B＝180°－∠A－∠ACB＝180°－50°－100°＝30°.

知识点2　线段垂直平分线的判定

3．如图，分别以线段AB的两端点A，B为圆心，大于  AB长为半径画弧，在线段AB的两侧分别交于点E，F，作直线EF交AB于点O.在直线EF上任取一点P(不与O重合)，连接PA，PB，则下列结论不一定成立的是(　C　)

A．PA＝PB      B．OA＝OB

C．OP＝OF      D．PO⊥AB

【解析】由作图可知，EF垂直平分AB，∴PA＝PB，故A选项正确；OA＝OB，故B选项正确；OE＝OF，故C选项错误；PO⊥AB，故D选项正确．

4．(八上教材P62练习T2改编)(2020·厦门期中)如图，AB＝AC，DB＝DC，E是AD延长线上一点，求证：BE＝CE.

【证明】连接BC，∵AB＝AC，DB＝DC，

∴A在线段BC的垂直平分线上，D在线段BC的垂直平分线上，

即AD是线段BC的垂直平分线，

∵E在直线AD上，∴BE＝CE.

知识点3　线段垂直平分线的作法

5．如图，在△ABC中，分别以点A，B为圆心，大于   AB长为半径画弧，两弧分别交于点D，E，则直线DE是(　D　)

A.∠A的平分线

B．AC边的中线

C．BC边的高线

D．AB边的垂直平分线

【解析】∵分别以点A，B为圆心，大于   AB长为半径画弧，两弧分别交于点D，E，

∴DA＝DB，EA＝EB，

∴点D，E在线段AB的垂直平分线上．

6．(2020·宜昌中考)如图，点E，F，G，Q，H在一条直线上，且EF＝GH，按如图所作的直线l为线段FG的垂直平分线．下列说法正确的是(　A　)

A．l是线段EH的垂直平分线

B．l是线段EQ的垂直平分线

C．l是线段FH的垂直平分线

D．EH是l的垂直平分线

【解析】A.∵直线l为线段FG的垂直平分线，

∴FO＝GO，l⊥FG，

∵EF＝GH，

∴EF＋FO＝OG＋GH，

即EO＝OH，

∴l为线段EH的垂直平分线；

B．∵EO≠OQ，∴l不是线段EQ的垂直平分线；

C．∵FO≠OH，∴l不是线段FH的垂直平分线；

D.∵l为直线，EH不能平分直线l，

∴EH不是l的垂直平分线．

知识点4　作对称轴

7．(教材P64练习T1改编)如图，先找出下列各图形中的轴对称图形，再画出它们的对称轴(有几条画几条).

【解析】(1)不是轴对称图形，没有对称轴．

(2)，(3)，(4)，(5)是轴对称图形，对称轴如图所示：

8.△ABC和△A′B′C′关于直线MN对称，△A′B′C′和△A″B″C″关于直线EF对称．

(1)画出直线EF；

(2)直线MN与EF相交于点O，试探究∠BOB″与直线MN，EF所夹锐角α的数量关系．

【解析】(1)如图，连接B′B″，

作线段B′B″的垂直平分线EF，

则直线EF是△A′B′C′和△A″B″C″的对称轴；

(2)连接B′O.

∵△ABC和△A′B′C′关于MN对称，

∴∠BOM＝∠B′OM.

又∵△A′B′C′和△A″B″C″关于EF对称，

∴∠B′OE＝∠B″OE.

∴∠BOB″＝∠BOM＋∠B′OM＋∠B′OE＋∠B″OE＝2(∠B′OM＋∠B′OE)＝2α.

即∠BOB″＝2α.

　　　　　　　　　　 关键能力·综合练

9．如图，在△ABC中，AB，BC的垂直平分线交于点O，且OA＝4，则OC的长为(　B　)

A．5     B．4    C．3     D．2

【解析】∵点O在AB的垂直平分线上，

∴OA＝OB.

∵点O在BC的垂直平分线上，

∴OC＝OB.∴OC＝OA＝4.

10．(2021·安徽模拟)如图，△ABC中，AD是BC的垂直平分线，则下列结论中不一定正确的是(　D　)

A.∠B＝∠C        B．AB＝AC

C．AD平分∠BAC      D．AB＝2BD

【解析】∵D是BC的中点，∴BD＝CD，

∵AD⊥BC，∴∠ADB＝∠ADC＝90°，

∴△ABD≌△ACD(SAS)，

∴∠B＝∠C，AB＝AC，∠BAD＝∠CAD，

即AD平分∠BAC.

11．(2021·大庆模拟)已知如图，AC是线段BD的垂直平分线，则图中全等三角形的对数是(　C　)

A.1对    B．2对    C．3对    D．4对

【解析】∵AC为线段BD的垂直平分线，∴AD＝AB，DC＝BC，且AC⊥BD，可以判定Rt△AOB≌Rt△AOD，Rt△COD≌Rt△COB，△ADC≌△ABC.

12．(2020·青海中考)如图，△ABC中，AB＝AC＝14 cm，AB的垂直平分线MN交AC于点D，且△DBC的周长是24 cm，则BC＝__10__cm.

【解析】∵C△DBC＝24 cm，

∴BD＋DC＋BC＝24 cm①，

又∵MN垂直平分AB，∴AD＝BD②，将②代入①得：AD＋DC＋BC＝24 cm，即AC＋BC＝24 cm，

又∵AC＝14 cm，∴BC＝24－14＝10 cm.

13．(教材P65习题13.1T6改编)(2020·十堰中考)如图，在△ABC中，DE是AC的垂直平分线．若AE＝3，△ABD的周长为13，则△ABC的周长为__19__．

【解析】∵DE是AC的垂直平分线，AE＝3，

∴AC＝2AE＝6，AD＝DC，

∵AB＋BD＋AD＝13，

∴△ABC的周长＝AB＋BC＋AC＝AB＋BD＋AD＋AC＝13＋6＝19.

14．(2020·宁夏中考)如图，在△ABC中，∠C＝84°，分别以点A，B为圆心，以大于AB的长为半径画弧，两弧分别交于点M，N，作直线MN交AC点D；以点B为圆心，适当长为半径画弧，分别交BA，BC于点E，F，再分别以点E，F为圆心，大于EF的长为半径画弧，两弧交于点P，作射线BP，此时射线BP恰好经过点D，则∠A＝__32__度．

【解析】由作图可得MN是线段AB的垂直平分线，BD是∠ABC的平分线，

∴AD＝BD，∠ABD＝∠CBD＝∠ABC，

∴∠A＝∠ABD，

∴∠A＝∠ABD＝∠CBD，

∵∠A＋∠ABC＋∠C＝180°，且∠C＝84°，

∴∠A＋2∠ABD＝180°－∠C，

即3∠A＝180°－84°，∴∠A＝32°.

15．(2021·珠海期中)如图，在△ABC中，∠C＝90°，DE是AB的垂直平分线．若∠BAD∶∠CAD＝2∶1，求∠B的度数．

【解析】∵DA＝DB，∴∠BAD＝∠B，

设∠CAD＝x，则∠BAD＝∠B＝2x，

∵∠C＝90°，

∴∠CAB＋∠B＝90°，

即x＋2x＋2x＝90°，

解得x＝18°，

∴∠B＝2x＝36°.

16．如图，△ABC中，∠ACB＝90°，AD平分∠BAC，DE⊥AB于点E.

(1)若∠BAC＝50°，求∠EDA的度数．

(2)求证：直线AD是线段CE的垂直平分线．

【解析】(1)∵∠BAC＝50°，AD平分∠BAC，

∴∠EAD＝∠BAC＝25°，

∵DE⊥AB，∴∠AED＝90°，

∴∠EDA＝90°－25°＝65°.

(2)∵DE⊥AB，

∴∠AED＝90°＝∠ACB，

又∵AD平分∠BAC，

∴∠DAE＝∠DAC，

∵AD＝AD，

∴△AED≌△ACD，

∴AE＝AC，

∵AD平分∠BAC，

∴AD⊥CE，即直线AD是线段CE的垂直平分线．

17．(素养提升题)(2021·芜湖期中)如图所示，在△ABC中，AB，AC的垂直平分线分别交BC于D，E，垂足分别是M，N.

(1)若△ADE的周长为6，求BC的长；

(2)若∠BAC＝100°，求∠DAE的度数．

【解析】(1)∵DM和EN分别垂直平分AB和AC，

∴AD＝BD，EA＝EC，

∵△ADE的周长为6，

∴AD＋DE＋EA＝6.

∴BD＋DE＋EC＝6，即BC＝6；

(2)∵DM和EN分别垂直平分AB和AC，

∴AD＝BD，EA＝EC，

∴∠B＝∠BAD＝  ∠ADE，

∠C＝∠EAC＝  ∠AED，

∵∠BAC＝∠BAD＋∠DAE＋∠EAC＝∠B＋∠DAE＋∠C＝100°，

∴∠B＋∠C＝100°－∠DAE，

在△ADE中，∠DAE＝180°－(∠ADE＋∠AED)＝180°－(2∠B＋2∠C)，

∴∠DAE＝180°－2(100°－∠DAE)，

∴∠DAE＝20°.

模型　线段垂直平分线性质的应用模型

在△ABC中，AB的中垂线DE交AC于F，垂足为D，若AC＝6，BC＝4，求△BCF的周长．

【解析】∵AB的中垂线DE交AC于F，∴AF＝BF.

又∵AC＝6，BC＝4，

∴△BCF的周长＝BC＋CF＋FB＝BC＋CF＋FA＝BC＋AC＝10.

应用模型：

如图，∵直线l⊥AB，垂足为点C，且AC＝BC，点P在直线l上，∴PA＝PB.

关闭Word文档返回原板块