

+江苏省南通市崇川区启秀中学2023-2024学年八年级上学期开学数学试卷
展开2023-2024学年江苏省南通市崇川区启秀中学八年级(上)开学数学试卷
一、单选题(每题2分,共20分)
1.(2分)下列一组数﹣8,,0,2,0.010010001…(相邻两个1之间依次增加一个0),其中无理数的个数有( )
A.0个 B.1个 C.2个 D.3个
2.(2分)下列调查中,最适合采用全面调查的是( )
A.了解全国中学生的睡眠时间
B.了解某河流的水质情况
C.调查全班同学的视力情况
D.了解一批灯泡的使用寿命
3.(2分)如图,直线a∥b,且直线a,d所截,则下列条件不能判定直线c∥d的是( )
A.∠3=∠4 B.∠1+∠5=180° C.∠1=∠2 D.∠1=∠4
4.(2分)如图,已知AB=AC,AE=AD,还需要添加的一个条件是( )
A.∠B=∠C B.BD=CE C.∠BAD=∠CAE D.以上都不对
5.(2分)如图,数轴上的两点A、B对应的实数分别是a、b,则下列式子中成立的是( )
A.1﹣2a>1﹣2b B.﹣a<﹣b C.a+b<0 D.|a|﹣|b|>0
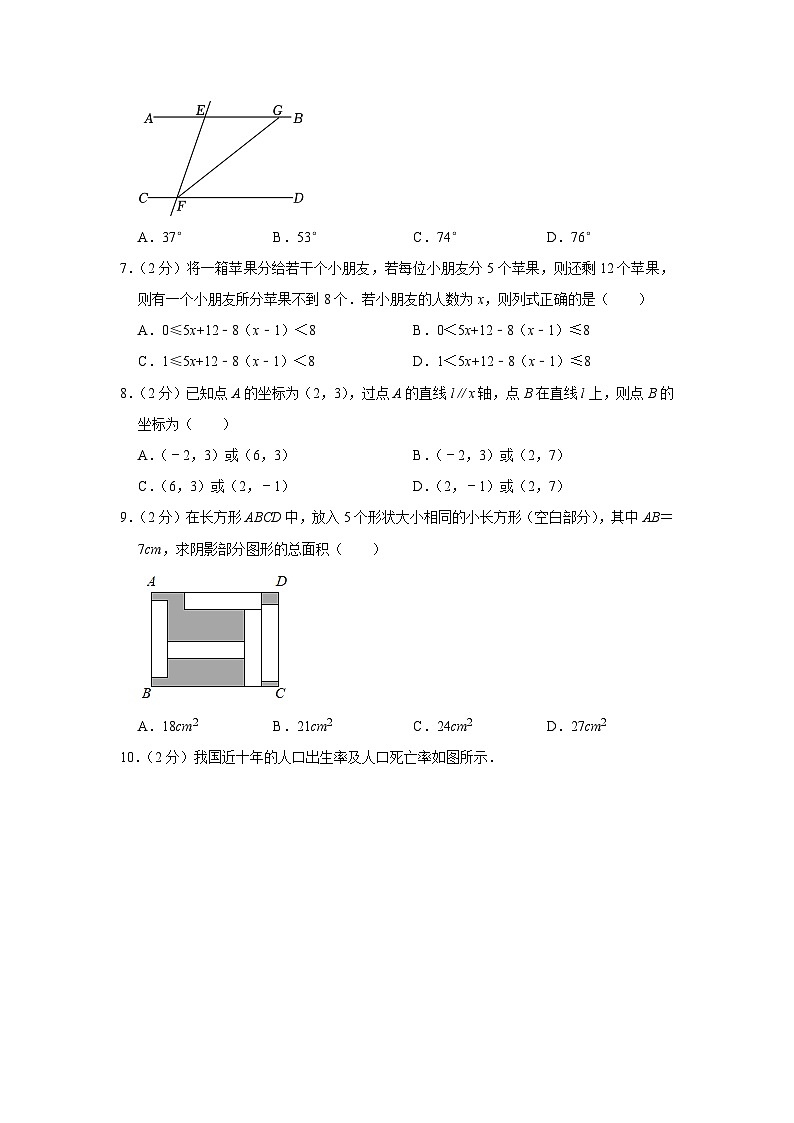
6.(2分)如图,平行线AB,CD被直线EF所截,若∠EFD=74°,则∠EGF的度数是( )
A.37° B.53° C.74° D.76°
7.(2分)将一箱苹果分给若干个小朋友,若每位小朋友分5个苹果,则还剩12个苹果,则有一个小朋友所分苹果不到8个.若小朋友的人数为x,则列式正确的是( )
A.0≤5x+12﹣8(x﹣1)<8 B.0<5x+12﹣8(x﹣1)≤8
C.1≤5x+12﹣8(x﹣1)<8 D.1<5x+12﹣8(x﹣1)≤8
8.(2分)已知点A的坐标为(2,3),过点A的直线l∥x轴,点B在直线l上,则点B的坐标为( )
A.(﹣2,3)或(6,3) B.(﹣2,3)或(2,7)
C.(6,3)或(2,﹣1) D.(2,﹣1)或(2,7)
9.(2分)在长方形ABCD中,放入5个形状大小相同的小长方形(空白部分),其中AB=7cm,求阴影部分图形的总面积( )
A.18cm2 B.21cm2 C.24cm2 D.27cm2
10.(2分)我国近十年的人口出生率及人口死亡率如图所示.
已知人口自然增长率=人口出生率﹣人口死亡率,下列判断错误的是( )
A.与2012年相比,2021年的人口出生率下降了近一半
B.近十年的人口死亡率基本稳定
C.近五年的人口总数持续下降
D.近五年的人口自然增长率持续下降
二、填空题(每题2分,共16分)
11.(2分)若>2是关于x的一元一次不等式,则a= .
12.(2分)一个多边形外角和是内角和的,则这个多边形的边数为 .
13.(2分)某班40名学生体重的频数分布直方图(不完整)如图所示,组距为 kg.
14.(2分)若第二象限内的点P(x,y)满足|x|=3,y2=25,则点P的坐标是 .
15.(2分)已知,∠AOB和∠BOC互为邻补角,且∠BOC:∠AOB=4:1,射线OE⊥OD,则∠BOE= .
16.(2分)如图,已知AC与BF相交于点E,AB∥CF,若CF=6,AD=4 .
17.(2分)已知关于x,y的二元一次方程组(a是常数),若不论a取什么实数(k是常数)的值始终不变,则k= .
18.(2分)如图,在三角形ABC中,BC=8cm,所得图形对应为三角形DEF,设平移的时间为t秒 时,AD=2CE.
三、解答题(第19题10分,20-21题6分,第22-25题8分,第26题10分,共60分)
19.(10分)(1)计算:﹣12+×()2+|1﹣|;
(2)解方程组:;
(3)解不等式组,并求出它的所有整数解的和.
20.(6分)如图,在平面直角坐标系中,A,B坐标分别为A(0,a),B(b,a),b满足(a﹣3)2+|b﹣5|=0,现同时将点A,B分别向下平移3个单位,分别得到点A,B的对应点C,BD,AB.
(1)求点C,D的坐标及四边形ABDC的面积S四边形ABCD;
(2)在y轴上是否存在一点M,连接MC,MD△MCD=S四边形ABCD?若存在这样一点,求出点M的坐标;若不存在
21.(6分)某校在九年级学生中随机抽取了若干名学生参加“平均每天体育运动时间”的调查,根据调查结果绘制了如下不完整的频数分布表和频数分布直方图.
频数分布表
运动时间t/min
频数
频率
30≤t<60
4
0.1
60≤t<90
7
0.175
90≤t<120
a
0.35
120≤t<150
9
0.225
150≤t<180
6
b
合计
n
1
请根据图表中的信息解答下列问题:
(1)频数分布表中的a= ,b= ,n= ;
(2)请补全频数分布直方图;
(3)若该校九年级共有480名学生,试估计该校九年级学生平均每天体育运动时间不低于120min的学生人数.
22.(8分)如图,在三角形ABC中,CD⊥AB于D,FE⊥AB于E交AC于点H,点G是BC延长线上一点,∠ACD+∠F=180°.
(1)求证:AC∥FG;
(2)若∠A=45°,∠BCD:∠ACD=2:3,求∠BCD的度数.
23.(8分)如图,在△ABC中,点D在边BC上,DE∥AB,∠DCE=∠A.
求证:CD=AB.
24.(8分)某中学为落实《教育部办公厅关于进一步加强中小学生体质管理的通知》文件要求,决定增设篮球、足球两门选修课程,需要购进一批篮球和足球.已知购买2个篮球和3个足球共需费用510元
(1)求篮球和足球的单价分别是多少元;
(2)学校计划采购篮球、足球共50个,并要求篮球不少于30个,且总费用不超过5500元.那么最多采购篮球多少个?
25.(8分)对m、n定义一种新运算“※”,规定:m※n=am﹣bn+5(a.b均为非零常数),等式右边的运算是通常的四则运算,3※(﹣1)=10.
(1)求a、b的值;
(2)若关于x的不等式组有且只有一个整数解,试求字母t的取值范围.
26.(10分)直线MN与直线PQ垂直相交于O,点A在射线OP上运动,点B在射线OM上运动.
(1)如图1,已知AE、BE分别是∠BAO和∠ABO角的平分线,点A、B在运动的过程中,请说明理由;若不发生变化;
(2)如图2,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及其延长线相交于E、F °;在△AEF中,如果有一个角是另一个角的3倍
2023-2024学年江苏省南通市崇川区启秀中学八年级(上)开学数学试卷
参考答案与试题解析
一、单选题(每题2分,共20分)
1.(2分)下列一组数﹣8,,0,2,0.010010001…(相邻两个1之间依次增加一个0),其中无理数的个数有( )
A.0个 B.1个 C.2个 D.3个
【分析】无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可求解.
【解答】解:在实数﹣8,,5,2,0.010010001…(相邻两个7之间依次增加一个0),中,8.010010001…(相邻两个1之间依次增加一个0).
故选:C.
【点评】本题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.
2.(2分)下列调查中,最适合采用全面调查的是( )
A.了解全国中学生的睡眠时间
B.了解某河流的水质情况
C.调查全班同学的视力情况
D.了解一批灯泡的使用寿命
【分析】根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似解答.
【解答】解:A.了解全国中学生的睡眠时间,故本选项不合题意;
B.了解某河流的水质情况,故本选项不合题意;
C.调查全班同学的视力情况,故本选项符合题意;
D.了解一批灯泡的使用寿命,故本选项不合题意;
故选:C.
【点评】本题考查的是抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
3.(2分)如图,直线a∥b,且直线a,d所截,则下列条件不能判定直线c∥d的是( )
A.∠3=∠4 B.∠1+∠5=180° C.∠1=∠2 D.∠1=∠4
【分析】根据平行线的判定定理进行一一分析.
【解答】解:A、若∠3=∠4时,两直线平行”可以判定c∥d;
B、若∠3+∠5=180°时,两直线平行”可以判定c∥d;
C、若∠1=∠3时,两直线平行”可以判定a∥b,符合题意;
D、由a∥b推知∠4+∠5=180°,则∠6+∠5=180°,两直线平行”可以判定c∥d.
故选:C.
【点评】本题主要考查了平行线的判定与性质,平行线的判定是由角的数量关系判断两直线的位置关系.平行线的性质是由平行关系来寻找角的数量关系.
4.(2分)如图,已知AB=AC,AE=AD,还需要添加的一个条件是( )
A.∠B=∠C B.BD=CE C.∠BAD=∠CAE D.以上都不对
【分析】根据BD=CE,利用“SSS”定理解答即可.
【解答】解:当BD=CE时,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SSS),
故选:B.
【点评】本题考查的是全等三角形的判定,熟练运用“SSS”定理是解题的关键.
5.(2分)如图,数轴上的两点A、B对应的实数分别是a、b,则下列式子中成立的是( )
A.1﹣2a>1﹣2b B.﹣a<﹣b C.a+b<0 D.|a|﹣|b|>0
【分析】依据点在数轴上的位置,不等式的性质,绝对值的意义,有理数大小的比较法则对每个选项进行逐一判断即可得出结论.
【解答】解:由题意得:a<b,
∴﹣2a>﹣2b,
∴7﹣2a>1﹣2b,
∴A选项的结论成立;
∵a<b,
∴﹣a>﹣b,
∴B选项的结论不成立;
∵﹣2<a<﹣1,2<b<3,
∴|a|<|b|,
∴a+b>0,
∴C选项的结论不成立;
∵﹣8<a<﹣1,2<b<3,
∴|a|<|b|,
∴|a|﹣|b|<0,
∴D选项的结论不成立.
故选:A.
【点评】本题主要考查了不等式的性质,绝对值的意义,有理数大小的比较法则,利用点在数轴上的位置确定出a,b的取值范围是解题的关键.
6.(2分)如图,平行线AB,CD被直线EF所截,若∠EFD=74°,则∠EGF的度数是( )
A.37° B.53° C.74° D.76°
【分析】先根据角平分线的定义求出∠GFD的度数,再由平行线的性质即可得出结论.
【解答】解:∵FG平分∠EFD,∠EFD=74°,
∴∠GFD=∠EFD=,
∵AB∥CD,
∴∠EGF=∠GFD=37°.
故选:A.
【点评】本题考查的是平行线的性质及角平分线的定义,熟知两直线平行,内错角相等是解题的关键.
7.(2分)将一箱苹果分给若干个小朋友,若每位小朋友分5个苹果,则还剩12个苹果,则有一个小朋友所分苹果不到8个.若小朋友的人数为x,则列式正确的是( )
A.0≤5x+12﹣8(x﹣1)<8 B.0<5x+12﹣8(x﹣1)≤8
C.1≤5x+12﹣8(x﹣1)<8 D.1<5x+12﹣8(x﹣1)≤8
【分析】根据每位小朋友分5个苹果,则还剩12个苹果;若每位小朋友分8个苹果,则有一个小朋友所分苹果不到8个.由此得出不等式组.
【解答】解:根据小朋友的人数为x,根据题意可得:
0≤5x+12﹣2(x﹣1)<8,
故选:A.
【点评】此题主要考查了一元一次不等式的应用,根据题意找出不等式的取值范围是解决问题的关键.
8.(2分)已知点A的坐标为(2,3),过点A的直线l∥x轴,点B在直线l上,则点B的坐标为( )
A.(﹣2,3)或(6,3) B.(﹣2,3)或(2,7)
C.(6,3)或(2,﹣1) D.(2,﹣1)或(2,7)
【分析】根据点A的坐标为(2,3),过点A的直线l∥x轴,点B在直线l上,且AB=4,可知点A的纵坐标为3,横坐标为:2+4=6或2﹣4=﹣2,然后即可得到点B的坐标.
【解答】解:∵点A的坐标为(2,3),点B在直线l上,
∴点A的纵坐标为7,横坐标为:2+4=4或2﹣4=﹣4,
即点A的坐标为(6,3)或(﹣6,
故选:A.
【点评】本题考查坐标与图形的性质,解答本题的关键是明确与x轴平行的直线上点的纵坐标相等.
9.(2分)在长方形ABCD中,放入5个形状大小相同的小长方形(空白部分),其中AB=7cm,求阴影部分图形的总面积( )
A.18cm2 B.21cm2 C.24cm2 D.27cm2
【分析】根据图形设小长方形的长为xcm,则宽为(7﹣x) cm,然后根据BC=一个小长方形的长+三个小长方形的宽列出方程,求出x后,再用大长方形的面积减去五个小长方形的面积即可.
【解答】解:(1)设小长方形的长为xcm,则宽为(7﹣x) cm,
由题意得:x+3(2﹣x)=11,
解得:x=5,
则7﹣x=4﹣5=2,
∴阴影部分图形的总面积=7×11﹣5×5×5=27(cm2),
故选:D.
【点评】本题考查了一元一次方程的应用,找准等量关系,正确列出一元一次方程是解题的关键.
10.(2分)我国近十年的人口出生率及人口死亡率如图所示.
已知人口自然增长率=人口出生率﹣人口死亡率,下列判断错误的是( )
A.与2012年相比,2021年的人口出生率下降了近一半
B.近十年的人口死亡率基本稳定
C.近五年的人口总数持续下降
D.近五年的人口自然增长率持续下降
【分析】根据折线统计图的信息解答即可.
【解答】解:由折线统计图可知,
A.与2012年相比,说法正确;
B.近十年的人口死亡率基本稳定,故本选项不合题意;
C.近五年的人口总数持续下降,五年的人口总数增长速度变缓;
D.近五年的人口自然增长率持续下降,故本选项不合题意;
故选:C.
【点评】本题考查了折线统计图,掌握人口自然增长率的定义是解答本题的关键.
二、填空题(每题2分,共16分)
11.(2分)若>2是关于x的一元一次不等式,则a= ﹣2 .
【分析】根据一元一次不等式的未知数x的次数等于1,系数不等于0即可得出答案.
【解答】解:∵是关于x的一元一次不等式,
∴a2﹣2=1且a﹣2≠3,
解得:a=﹣2,
故答案为:﹣2.
【点评】本题考查了一元一次不等式的定义,掌握一元一次不等式的未知数x的次数等于1,系数不等于0是解题的关键.
12.(2分)一个多边形外角和是内角和的,则这个多边形的边数为 11 .
【分析】多边形的内角和定理为(n﹣2)×180°,多边形的外角和为360°,根据题意列出方程求出n的值.
【解答】解:设这个多边形的边数为n,
根据题意可得:,
解得:n=11,
故答案为:11.
【点评】本题主要考查的是多边形的内角和公式以及外角和定理,属于基础题型.记忆理解并应用这两个公式是解题的关键.
13.(2分)某班40名学生体重的频数分布直方图(不完整)如图所示,组距为 5 kg.
【分析】根据频数分布直方图计算即可.
【解答】解:组距为=5(kg).
故答案为:5.
【点评】本题考查了频数分布直方图,读频数分布直方图的能力和利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
14.(2分)若第二象限内的点P(x,y)满足|x|=3,y2=25,则点P的坐标是 (﹣3,5) .
【分析】根据绝对值的意义和平方根得到x=±3,y=±5,再根据第二象限的点的坐标特点得到x<0,y>0,于是x=﹣3,y=5,然后可直接写出P点坐标.
【解答】解:∵|x|=3,y2=25,
∴x=±4,y=±5,
∵第二象限内的点P(x,y),
∴x<0,y>2,
∴x=﹣3,y=5,
∴点P的坐标为(﹣3,5),
故答案为:(﹣3,8).
【点评】本题考查了各象限内点的坐标的符号特征以及解不等式,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).
15.(2分)已知,∠AOB和∠BOC互为邻补角,且∠BOC:∠AOB=4:1,射线OE⊥OD,则∠BOE= 72°或108° .
【分析】根据平角的意义、角平分线的意义,邻补角,垂直的意义,分别计算各个角的大小即可.
【解答】解:∵∠AOB和∠BOC互为邻补角,
∴∠AOB+∠BOC=180°,
又∵∠BOC:∠AOB=4:1,
∴∠BOC=180°×=144°=36°,
∵射线OD平分∠AOB,
∴∠AOD=∠BOD=∠AOB=18°,
∵OE⊥OD,
∴∠DOE=90°,
如图8,∠BOE=∠DOE﹣∠BOD=90°﹣18°=72°,
如图2,∠BOE=∠DOE+∠BOD=90°+18°=108°,
故答案为:72°或108°.
【点评】本题考查平角的意义、角平分线的意义,邻补角,垂直的意义,通过图形直观得出各个角之间的关系是正确计算的前提.
16.(2分)如图,已知AC与BF相交于点E,AB∥CF,若CF=6,AD=4 2 .
【分析】利用全等三角形的判定定理和性质定理可得结果.
【解答】解:∵AB∥CF,
∴∠A=∠FCE,
∠B=∠F,
∵点E为BF中点,
∴BE=FE,
在△ABE与△CFE中,
,
∴△ABE≌△CFE(AAS),
∴AB=CF=6,
∵AD=4,
∴BD=5,
故答案为:2.
【点评】本题主要考查了全等三角形的判定定理和性质定理,熟练掌握定理是解答此题的关键.
17.(2分)已知关于x,y的二元一次方程组(a是常数),若不论a取什么实数(k是常数)的值始终不变,则k= ﹣1 .
【分析】将方程组中的两个方程变形后联立消掉a即可得出结论.
【解答】解:∵(a是常数),
∴8x+8y+x﹣3y=﹣6a+4+4a+8,
即x+y=2,
∴﹣x﹣y=﹣2,
故答案为:﹣6.
【点评】本题主要考查二元一次方程组的应用,将方程组中的两个方程联立消掉a是解题的关键.
18.(2分)如图,在三角形ABC中,BC=8cm,所得图形对应为三角形DEF,设平移的时间为t秒 8或 时,AD=2CE.
【分析】情况一:当点E移点C右侧时,根据平移的性质可知AD=CF=CE+EF=2CE,EF=BC=CE=8,可得t;
情况二:当点E在点B,点C之间时,可知AD=BE=CF=2CE,BC=BE+CE=BE+BE=8,可得BE=,可得t.
【解答】解:情况一:当点E移点C右侧时,
∵AD=CF=CE+EF=2CE,
BC=EF,
∴CE=EF=BC=8,
∴CF=7×8=16,
∴t=16÷2=3,
∴当t=8时,AD=2CE;
情况二:当点E在点B,点C之间时,
∵AD=BE=CF=6CE,
∴BC=BE+CE=BE+BE=3,
∴BE=,
∴t=÷2=,
当t=时,AD=2CE;
故答案为:2,.
【点评】本题主要考查了平移的性质,根据平移的性质得出CF的长是解答此题的关键.
三、解答题(第19题10分,20-21题6分,第22-25题8分,第26题10分,共60分)
19.(10分)(1)计算:﹣12+×()2+|1﹣|;
(2)解方程组:;
(3)解不等式组,并求出它的所有整数解的和.
【分析】(1)先计算平方,立方根,绝对值,再计算加减法;
(2)根据加减消元法解方程即可求解;
(3)根据解一元一次不等式组的方法求出不等式组的整数解,即可求解.
【解答】解:(1)﹣12+×()8+|1﹣|
=﹣5+4×+﹣1
=﹣7+1+﹣7
=﹣1;
(2),
①×7+②,得9x=18,
解得x=2,
将x=6代入①得:8+y=10,
解得y=2,
∴原方程组的解为;
(3),
解不等式①得:x≤5,
解不等式②得:x>﹣,
∴不等式组解集为:﹣<x≤5,
∴它的整数解有:﹣5,﹣1,0,2,2,3,7,5,
∴它们的和为﹣2﹣7+0+1+2+3+4+7=12.
【点评】本题主要考查解一元一次不等式组,一元一次不等式组的整数解,掌握不等式的性质,解不等式的方法,不等式组的取值方法是解题的关键.同时考查了实数的运算,解二元一次方程组.
20.(6分)如图,在平面直角坐标系中,A,B坐标分别为A(0,a),B(b,a),b满足(a﹣3)2+|b﹣5|=0,现同时将点A,B分别向下平移3个单位,分别得到点A,B的对应点C,BD,AB.
(1)求点C,D的坐标及四边形ABDC的面积S四边形ABCD;
(2)在y轴上是否存在一点M,连接MC,MD△MCD=S四边形ABCD?若存在这样一点,求出点M的坐标;若不存在
【分析】(1)由偶次方及绝对值的非负性可求出a、b的值,进而即可得出点A、B的坐标,再根据平移的性质可得出点C、D的坐标;根据坐标与图形的性质求出S四边形ABCD;
(2)设M坐标为(0,m),根据三角形的面积公式列出方程,解方程求出m,得到点M的坐标;
【解答】解:(1)∵(a﹣3)2+|b﹣3|=0,
∴a=3,b=8,
∴点A(0,3),8).
将点A,B分别向下平移3个单位,得到点C、D,
∴点C(﹣1,7),0).
∴S四边形ABDC=CD×OA=5×5=15;
(2)在y轴上存在一点M,使S△MCD=S四边形ABCD,
设M坐标为(6,m).
∵S△MCD=S四边形ABDC,
∴×5×|m|=,
解得m=±2,
∴M(7,2)或(0;
∴在y轴上存在点M(7,2)或(0,使S△MCD=S四边形ABCD.
【点评】本题综合考查了坐标与图形性质、三角形的面积、平行四边形的面积、平移以及非负性的运用,解题的关键是熟练掌握点的坐标与线段长度之间的转化.
21.(6分)某校在九年级学生中随机抽取了若干名学生参加“平均每天体育运动时间”的调查,根据调查结果绘制了如下不完整的频数分布表和频数分布直方图.
频数分布表
运动时间t/min
频数
频率
30≤t<60
4
0.1
60≤t<90
7
0.175
90≤t<120
a
0.35
120≤t<150
9
0.225
150≤t<180
6
b
合计
n
1
请根据图表中的信息解答下列问题:
(1)频数分布表中的a= 14 ,b= 0.15 ,n= 40 ;
(2)请补全频数分布直方图;
(3)若该校九年级共有480名学生,试估计该校九年级学生平均每天体育运动时间不低于120min的学生人数.
【分析】(1)根据“频率=频数÷总数”可得n的值,进而得出a、b的值;
(2)根据a的值即可补全频数分布直方图;
(3)利用样本估计总体解答即可.
【解答】解:(1)由题意可知,n=4÷0.2=40,
∴a=40×0.35=14,b=6÷40=3.15,
故答案为:14;0.15;
(2)补全频数分布直方图如下:
(3)480×=180(名),
答:估计该校九年级学生平均每天体育运动时间不低于120min的学生人数为180名.
【点评】本题考查频数分布表、频数分布直方图的意义和制作方法,从统计图表中获取数量和数量关系是正确计算的前提,样本估计总体是统计中常用的方法.
22.(8分)如图,在三角形ABC中,CD⊥AB于D,FE⊥AB于E交AC于点H,点G是BC延长线上一点,∠ACD+∠F=180°.
(1)求证:AC∥FG;
(2)若∠A=45°,∠BCD:∠ACD=2:3,求∠BCD的度数.
【分析】(1)根据平行线的性质和判定即可解答;
(2)根据直角三角形即可解答.
【解答】(1)证明:∵CD⊥AB,FE⊥AB,
∴∠AEH=∠ADC=90°,
∴EF∥DC,
∴∠ACD+∠CHE=180°,
∵∠ACD+∠F=180°,
∴∠F=∠CHE,
∴AC∥FG;
(2)解:∵∠BCD:∠ACD=2:3,
设∠BCD=6x,∠ACD=3x,
∵CD⊥AB,
∴∠ADC=90°,
∴∠A+∠ACD=90°,
即45°+3x=90°,
解得x=15°,
∴∠BCD=30°.
【点评】本题考查了平行线的性质和判定,掌握平行线的性质和判定是解题的关键.
23.(8分)如图,在△ABC中,点D在边BC上,DE∥AB,∠DCE=∠A.
求证:CD=AB.
【分析】利用平行线的性质得∠EDC=∠B,再利用ASA证明△CDE≌△ABC,可得结论.
【解答】证明:∵DE∥AB,
∴∠EDC=∠B,
在△CDE和△ABC中,
,
∴△CDE≌△ABC(ASA),
∴CD=AB.
【点评】本题主要考查了平行线的性质,全等三角形的判定与性质等知识,熟练掌握全等三角形的判定与性质是解题的关键.
24.(8分)某中学为落实《教育部办公厅关于进一步加强中小学生体质管理的通知》文件要求,决定增设篮球、足球两门选修课程,需要购进一批篮球和足球.已知购买2个篮球和3个足球共需费用510元
(1)求篮球和足球的单价分别是多少元;
(2)学校计划采购篮球、足球共50个,并要求篮球不少于30个,且总费用不超过5500元.那么最多采购篮球多少个?
【分析】(1)根据购买2个篮球和3个足球共需费用510元;购买3个篮球和5个足球共需费用810元,可以列出相应的二元一次方程组,然后求解即可;
(2)根据要求篮球不少于30个,且总费用不超过5500元,可以列出相应的不等式组,从而可以求得篮球数量的取值范围,然后即可写出相应的购买方案.
【解答】解:(1)设篮球的单价为a元,足球的单价为b元,
由题意可得:,
解得,
答:篮球的单价为120元,足球的单价为90元;
(2)设采购篮球x个,则采购足球为(50﹣x)个,
∵要求篮球不少于30个,且总费用不超过5500元,
∴,
解得30≤x≤33,
∵x为整数,
∴x的值可为30,31,33,
∴共有四种购买方案,
方案一:采购篮球30个,采购足球20个;
方案二:采购篮球31个,采购足球19个;
方案三:采购篮球32个,采购足球18个;
方案四:采购篮球33个,采购足球17个.
【点评】本题考查二元一次方程组的应用、一元一次不等式组的应用,解答本题的关键是明确题意,列出相应的方程组和不等式组.
25.(8分)对m、n定义一种新运算“※”,规定:m※n=am﹣bn+5(a.b均为非零常数),等式右边的运算是通常的四则运算,3※(﹣1)=10.
(1)求a、b的值;
(2)若关于x的不等式组有且只有一个整数解,试求字母t的取值范围.
【分析】(1)已知等式利用题中的新定义化简,计算即可求出a与b的值;
(2)已知不等式组利用题中的新定义化简,把a与b的值代入后,根据不等式组有且只有一个整数解,确定出t的范围即可.
【解答】解:(1)∵2※3=8,3※(﹣1)=10,
∴,
解得:;
(2)∵不等式组,且a=2,
∴ax﹣b(2x﹣3)+6=﹣3x+11<9,7ax+6b+5=4x+17<t,
解得:,
∵关于x的不等式组有且只有一个整数解,
∴1<≤5,
解得:20<t≤23,
∴t的取值范围是20<t≤23.
【点评】此题考查了一元一次不等式组的整数解,解二元一次方程组,以及解一元一次不等式,弄清题中的新定义是解本题的关键.
26.(10分)直线MN与直线PQ垂直相交于O,点A在射线OP上运动,点B在射线OM上运动.
(1)如图1,已知AE、BE分别是∠BAO和∠ABO角的平分线,点A、B在运动的过程中,请说明理由;若不发生变化;
(2)如图2,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及其延长线相交于E、F 90 °;在△AEF中,如果有一个角是另一个角的3倍
【分析】(1)根据直线MN与直线PQ垂直相交于O可知∠AOB=90°,再由AE、BE分别是∠BAO和∠ABO角的平分线得出∠BAE=∠OAB,∠ABE=∠ABO,由三角形内角和定理即可得出结论;
(2)由∠BAO与∠BOQ的角平分线相交于E可知∠EAO=∠BAO,∠EOQ=∠BOQ,进而得出∠E的度数,由AE、AF分别是∠BAO和∠OAG的角平分线可知∠EAF=90°,在△AEF中,由一个角是另一个角的3倍分四种情况进行分类讨论.
【解答】解:(1)∠AEB的大小不变,
∵直线MN与直线PQ垂直相交于O,
∴∠AOB=90°,
∴∠OAB+∠OBA=90°,
∵AE、BE分别是∠BAO和∠ABO角的平分线,
∴∠BAE=∠OAB∠ABO,
∴∠BAE+∠ABE=(∠OAB+∠ABO)=,
∴∠AEB=135°;
(2)∵AE、AF分别是∠BAO和∠OAG的角平分线,
∴∠EAO=∠BAO∠GAO,
∴∠EAF=(∠BAO+∠GAO)=.
故答案为:90;
∵∠BAO与∠BOQ的角平分线相交于E,
∴∠EAO=∠BAO∠BOQ,
∴∠E=∠EOQ﹣∠EAO=(∠BOQ﹣∠BAO)=,
即∠ABO=2∠E,
在△AEF中,∵有一个角是另一个角的3倍
①∠EAF=6∠E,∠E=30°;
②∠EAF=3∠F,∠E=60°;
③∠F=3∠E,∠E=22.7°;
④∠E=3∠F,∠E=67.5°.
∴∠ABO为60°或45°.
【点评】本题考查的是三角形内角和定理、三角形外角性质以及角平分线的定义的运用,熟知三角形内角和是180°是解答此题的关键.
声明:试题解析著作权属所有,未经书面同意,不得复制发布日期:2023/9/13 14:44:04;用户:娄老师;邮箱:15225657626;学号:48669677
2023-2024学年南通市崇川区启秀中学八上数学期末质量跟踪监视试题含答案: 这是一份2023-2024学年南通市崇川区启秀中学八上数学期末质量跟踪监视试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号,已知反比例函数图像经过点,下列各数中是无理数的是等内容,欢迎下载使用。
2022~2023学年江苏省南通市崇川区启秀中学八年级(上)第一次月考数学试卷(含解析): 这是一份2022~2023学年江苏省南通市崇川区启秀中学八年级(上)第一次月考数学试卷(含解析),共9页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
江苏省南通市崇川区南通市启秀中学2023-2024学年八年级上学期12月月考数学试题: 这是一份江苏省南通市崇川区南通市启秀中学2023-2024学年八年级上学期12月月考数学试题,共4页。












