《三角形内角和定理的证明》PPT课件1-八年级上册数学北师大版

这是一份《三角形内角和定理的证明》PPT课件1-八年级上册数学北师大版，共9页。
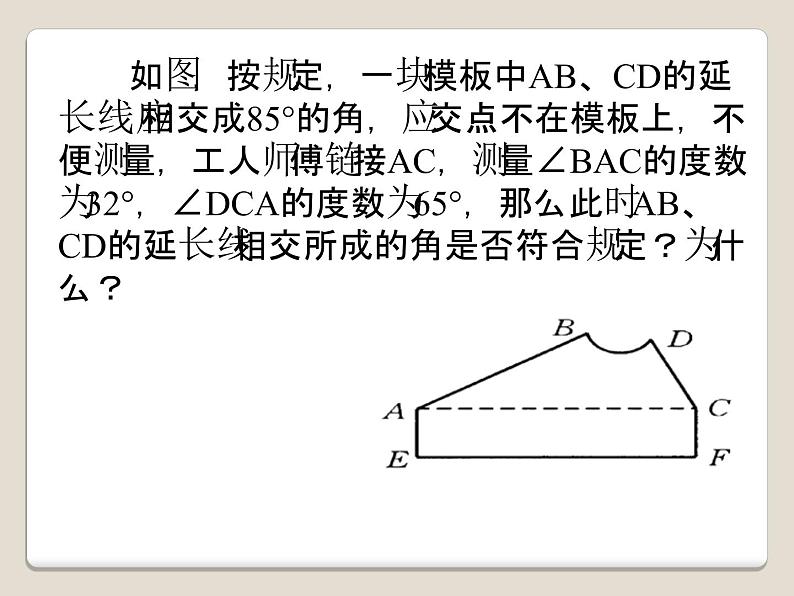
三角形内角和定理的证明八年级上册北京师范大学出版社学习目标:1、掌握三角形内角和定理的证明及其的简单应用．2、能够通过作辅助线证明三角形内角和定理.课前小测：1．三角形的内角和是　　　　。直角三角形的两锐角和是　　　　.2．在△ABC中，∠A=63°，∠C=36°，则∠B= °. 如图，按规定，一块模板中AB、CD的延长线应相交成85°的角，应交点不在模板上，不便测量，工人师傅链接AC，测量∠BAC的度数为32°，∠DCA的度数为65°，那么此时AB、CD的延长线相交所成的角是否符合规定？为什么？ 我们已经知道三角形的内角和为180 °这一基本事实，这个结论我们是如何得到的呢？归纳总结定理证明：根据所给的图，写出已知，求证，并给出证明.已知：求证：证明：定理应用：在△ABC中，∠B=38°，∠C=62°，AD是△ABC的角平分线，求∠ADB的度数．练一练：1、下列叙述正确的是（ ）．A．钝角三角形的内角和大于锐角三角形的内角和 B．三角形两个内角的和一定大于第三个内角C．三角形中至少有两个锐角 D．三角形中至少有一个锐角2、△ABC中，∠C=90°，∠A=30°，∠B= ．3、∠A=50°，∠B=∠C，则△ABC中∠B= ．4、如图：∠A=32°,∠B=44°,∠D=48°,则∠C= ．