初中数学北师大版七年级上册3.5 探索与表达规律课后作业题

这是一份初中数学北师大版七年级上册3.5 探索与表达规律课后作业题，共8页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
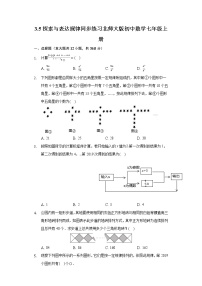
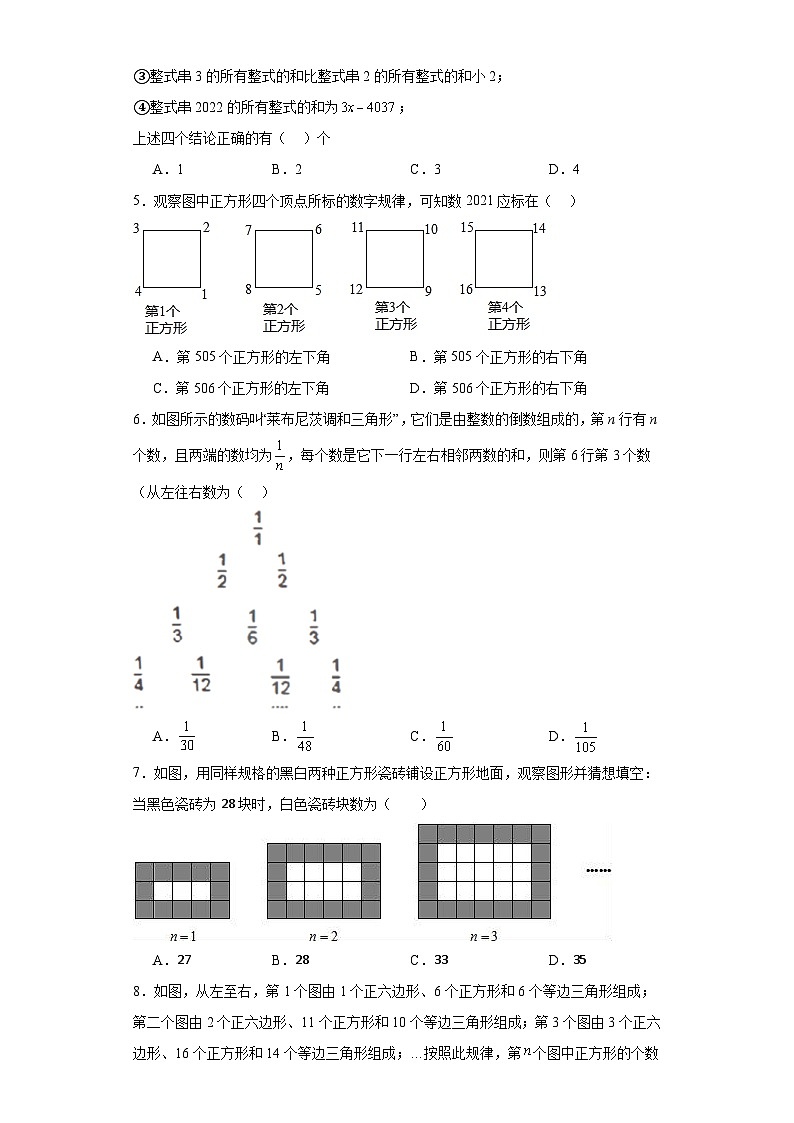
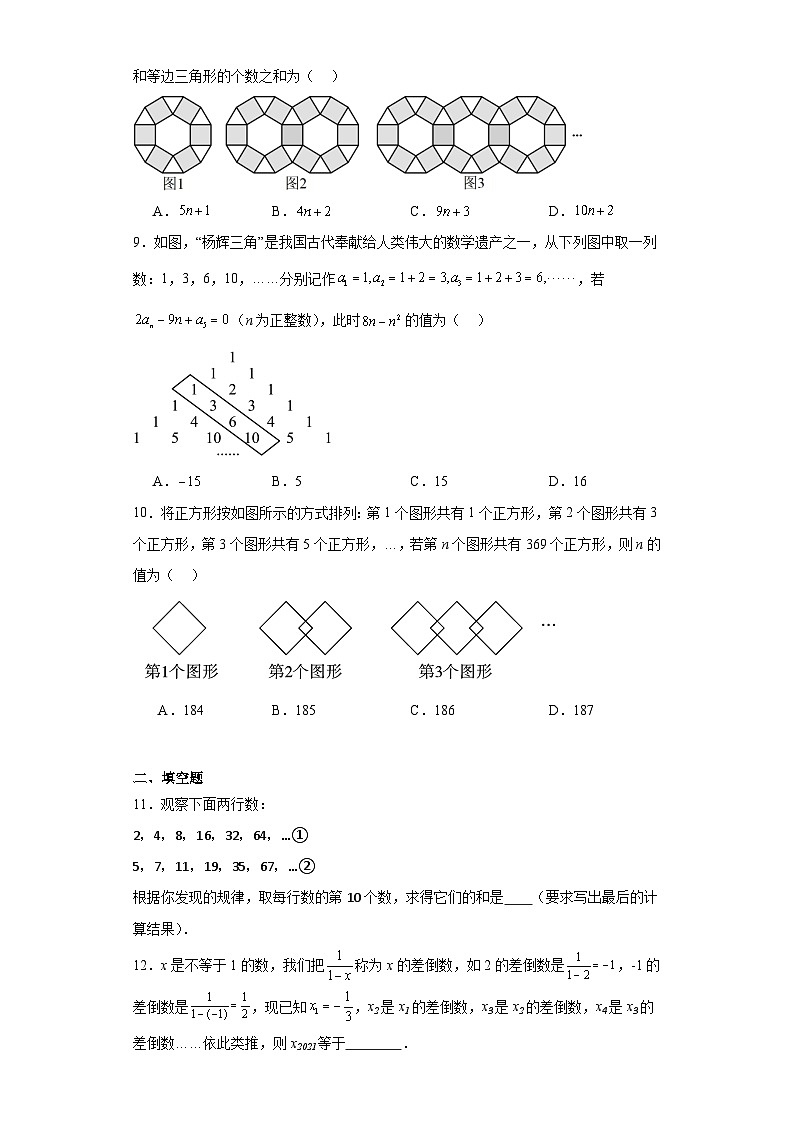
3.5探索与表达规律提升练习-北师大版数学七年级上册学校:___________姓名：___________班级：___________考号：___________ 一、单选题1．一个机器人从数轴的原点出发，沿数轴的正方向，以每前进步后退步的程序运动，设该机器人每秒前进或后退步，并且每步的距离为个单位长度，表示第秒时该机器人在数轴上的位置所对应的数，现给出下列结论：①；②；③；④；⑤，其中错误的结论是（ ）A．②④⑤ B．①④ C．①③ D．③④2．如图所示，是由一组形状大小完全相同的梯形组成的图形，第n（n为正整数）个图形的周长记为，当n＝2021时，的值为（　　）A． B． C． D．3．如图是中国宋代的“贾宪三角”又称“杨辉三角”，比欧洲的“帕斯卡三角”早近600年，它揭示了二项式乘方展开式的系数规律．观察下列各式及其展开式，请猜想（a+b）10展开式中所有项的系数和是（　　）A．128 B．256 C．512 D．10244．有依次排列的3个整式：x，，，对任意相邻的两个整式，都用右边的整式减去左边的整式，所得之差写在这两个整式之间，可以产生一个新整式串：x，7，，，，则称它为整式串1；将整式串1按上述方式再做一次操作，可以得到整式串2；以此类推通过实际操作，得出以下结论：①整式串2为：x，，7，x，，，，，；②整式串3的和为；③整式串3的所有整式的和比整式串2的所有整式的和小2；④整式串2022的所有整式的和为；上述四个结论正确的有（    ）个A．1 B．2 C．3 D．45．观察图中正方形四个顶点所标的数字规律，可知数2021应标在（    ）A．第505个正方形的左下角 B．第505个正方形的右下角C．第506个正方形的左下角 D．第506个正方形的右下角6．如图所示的数码叫“莱布尼茨调和三角形”，它们是由整数的倒数组成的，第n行有n个数，且两端的数均为，每个数是它下一行左右相邻两数的和，则第6行第3个数（从左往右数为（    ）A． B． C． D．7．如图，用同样规格的黑白两种正方形瓷砖铺设正方形地面，观察图形并猜想填空：当黑色瓷砖为28块时，白色瓷砖块数为（　　）A．27 B．28 C．33 D．358．如图，从左至右，第1个图由1个正六边形、6个正方形和6个等边三角形组成；第二个图由2个正六边形、11个正方形和10个等边三角形组成；第3个图由3个正六边形、16个正方形和14个等边三角形组成；…按照此规律，第个图中正方形的个数和等边三角形的个数之和为（    ）A． B． C． D．9．如图，“杨辉三角”是我国古代奉献给人类伟大的数学遗产之一，从下列图中取一列数：1，3，6，10，……分别记作，若（n为正整数），此时的值为（    ）A． B．5 C．15 D．1610．将正方形按如图所示的方式排列：第1个图形共有1个正方形，第2个图形共有3个正方形，第3个图形共有5个正方形，…，若第n个图形共有369个正方形，则n的值为（    ）A．184 B．185 C．186 D．187 二、填空题11．观察下面两行数：2，4，8，16，32，64，…①5，7，11，19，35，67，…②根据你发现的规律，取每行数的第10个数，求得它们的和是     （要求写出最后的计算结果）．12．x是不等于1的数，我们把称为x的差倒数，如2的差倒数是，-1的差倒数是，现已知，x2是x1的差倒数，x3是x2的差倒数，x4是x3的差倒数……依此类推，则x2021等于          ．13．有一列具有规律的数字：，，，，…则这列数字第10个数为     ．14．用同样的火柴棒按如下图规律摆图，若摆第个（为正整数）图，则需要     根火柴棒（用含的代数式表示）15．如图，是一组按照某种规律摆放而成的图案，则图6中三角形的个数是        16．下列图形都是由同样大小的圆按照一定规律摆放而成，其中第①个图形有5个小圆，第②个图形有9个小圆，第③个图形有13个小圆，…，按此规律排列，则第n个图形中小圆的个数为        个．17．国数学家洛萨提出了一个猜想：如果n为奇数，我们计算3n+1；如果n为偶数，我们除以2，不断重复这样的运算，经过有限步骤后一定可以得到1．例如，n=5时，经过上述运算，依次得到一列数5，16，8，4，2，1．（ 注：计算到1结束），若n=12，得到一列数的和为       ；若小明同学对某个整数n，按照上述运算，得到一列数，已知第八个数为1，则整数n的所有可能取值中，最小的值为       ．18．有理数，我们把称为的差倒数．如：3的差倒数是，的差倒数是，如果，是的差倒数，是的差倒数，是的差倒数，，依此类推，那么  ，  ，  ．19．如图所示的图形是按一定规律排列的．则第5个图形中“○”的个数为           ，第n个图形中“○”的个数为           ．20．某同学的身份证号码为320922200502187913，则此人出生时间是                   ． 三、解答题21． 从2开始，连续的偶数相加，它们和的情况如下表：（1）如果n=8时，那么S的值为________；（2）由表中的规律猜想：用n的代数式表示S的公式为S=2+4+6+8+…+2n=_________；（3）由上题的规律计算300+302+304+…+2010+2012的值（要有计算过程）．22．用棋子摆出下列一组图形：（1）填写下表：图形编号123456图形中的棋子      （2）照这样的方式摆下去，写出摆第个图形棋子的枚数；（用含的代数式表示）.（3）试计算第672个图形棋子的枚数.23．如图，设A是由n×n个有理数组成的n行n列的数表，其中aij（i，j＝1，2，3，…，n）表示位于第i行第j列的数，且aij取值为1或﹣1．对于数表A给出如下定义：记xi为数表A的第i行各数之积，yj为数表A的第j列各数之积．令S＝（x1+x2+…+xn）+（y1+y2+…+yn），将S称为数表A的“积和”． a11a12 a1na21a22 a2nMM Man1an2 ann（1）当n＝4时，对如下数表A，求该数表的“积和”S的值；11﹣1﹣11﹣1111﹣1﹣11﹣1﹣111（2）是否存在一个3×3的数表A，使得该数表的“积和”S＝0？并说明理由；（3）当n＝10时，直接写出数表A的“积和”S的所有可能的取值．24．如图，在数轴上有三个点，点P、Q、M，其中点P所对应的数是最大的负整数，点Q所对应的数是倒数等于它本身的自然数，点M所对应的数x满足（x﹣5）2＝0．（1）写出点P、Q、M分别对应的数．P　 　；Q　 　；M　 　．（2）现对P点做如下移动：第1次向右移动1个单位长度至B点，第2次从B点向左移动3个单位长度至C点，第3次从C点向右移动6个单位长度至D点，第4次从D点向左移动9个单位长度至E点，…依此类推，这样移动6次后该点到原点的距离为 　 　个单位长度；移动2021次后该点到原点的距离为 　 　个单位长度．（3）现将点P向左移动a个单位长度，则得到的点对应的数为 　 　（请用含a的代数式表示），若将数轴折叠，使得Q点与M点重合，此时点P和10所对应的点重合，则a＝　 　25．观察下列有规律的数：，，，，，…根据规律可知（1）第7个数 ，第n个数是 （n是正整数）；（2）是第 个数；（3）计算++++…+．
参考答案：1．C2．C3．D4．C5．D6．C7．D8．C9．C10．B11．205112．/0.7513．14．7n+115．20.16．．17．     67     4或5或3218．          /0.5     219．     16     /20．2005年02月18日21．（1）72；（2）；（3）990692．22．（1）略；（2）；（3）201923．（1）0；（2）不存在；（3）﹣20，﹣16，﹣12，﹣8，﹣4，0，4，8，12，16，2024．（1）-1，1，5；（2）9；3030；（3）-1-a；325．（1）；；（2）11；（3）．