2023-2024学年山东省枣庄市滕州市张汪中学八年级（上）开学数学试卷（含解析）

这是一份2023-2024学年山东省枣庄市滕州市张汪中学八年级（上）开学数学试卷（含解析），共14页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2023-2024学年山东省枣庄市滕州市张汪中学八年级（上）开学数学试卷一、选择题（本大题共12小题，共36.0分。在每小题列出的选项中，选出符合题目的一项）1.  在实数，，，，，中，无理数的个数是(    )A.  B.  C.  D. 2.  下列计算正确的是(    )A.  B.
C.  D. 3.  若，为实数，且，则的值是(    )A.  B.  C.  D. 4.  估计的值在(    )A. 到之间 B. 到之间 C. 到之间 D. 到之间5.  如图中，，分别以边，，向外做正方形，正方形的面积为，正方形的面积为，则正方形的面积是(    )
 A.  B.  C.  D. 6.  如图，一棵大树被台风挂断，若树在离地面处这段，树顶端落在离树底部处，则树折断之前高(    )
 A.  B.  C.  D. 7.  如图所示，在数轴上点所表示的数为，则的值为(    )
A.  B.  C.  D. 8.  如图，数轴上表示的点应在(    )

 A. 线段上 B. 线段上 C. 线段上 D. 线段上9.  如图，有一张三角形纸片，两直角边，，将折叠，使点与重合，折痕为，则的长为(    )A.
B.
C.
D. 10.  的整数部分为，小数部分为，则的值为(    )A.  B.  C.  D. 11.  已知和是某正数的平方根，则的值是(    )A.  B.  C. 或 D. 或12.  如图一个三级台阶，它的每一级的长宽高分别是，和，和是这个台阶的两个相对的端点，点上有一只蚂蚁，想到点去吃可口的食物，则蚂蚁沿着台阶面爬到点的最短路程长为(    )
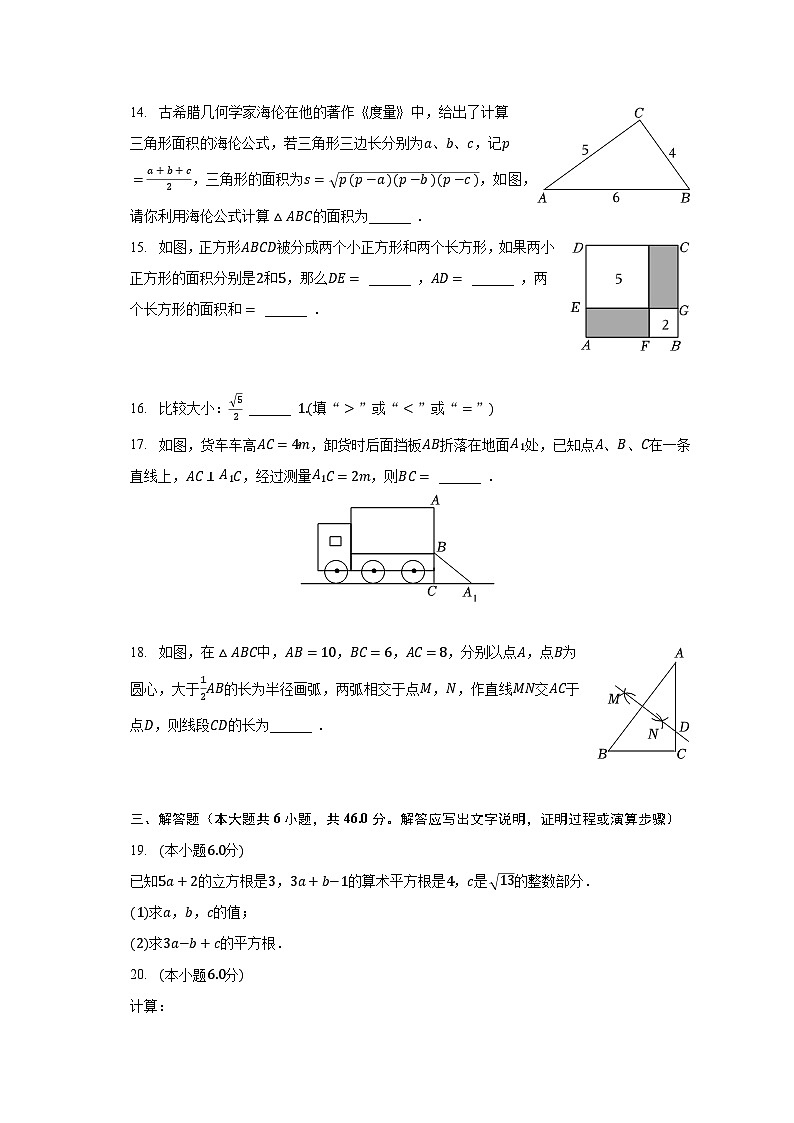
A.  B.  C.  D. 二、填空题（本大题共6小题，共18.0分）13.  已知，，则用、表示为______ ．14.  古希腊几何学家海伦在他的著作度量中，给出了计算三角形面积的海伦公式，若三角形三边长分别为、、，记，三角形的面积为，如图，请你利用海伦公式计算的面积为______ ．15.  如图，正方形被分成两个小正方形和两个长方形，如果两小正方形的面积分别是和，那么 ______ ， ______ ，两个长方形的面积和 ______ ．
 16.  比较大小： ______ 填“”或“”或“”17.  如图，货车车高，卸货时后面挡板折落在地面处，已知点、、在一条直线上，，经过测量，则 ______ ．
18.  如图，在中，，，，分别以点，点为圆心，大于的长为半径画弧，两弧相交于点，，作直线交于点，则线段的长为______ ．
 三、解答题（本大题共6小题，共46.0分。解答应写出文字说明，证明过程或演算步骤）19.  本小题分已知的立方根是，的算术平方根是，是的整数部分．求，，的值；求的平方根．20.  本小题分
计算：
；
．21.  本小题分一架方梯长米，如图所示，斜靠在一面上：若梯子底端离墙米，这个梯子的顶端距地面有多高？在的条件下，如果梯子的顶端下滑了米，那么梯子的底端在水平方向滑动了几米？22.  本小题分
观察下列各式及证明过程：
；；．
验证：；．
按照上述等式及验证过程的基本思想，请写出两个类似的等式，并选择其中一个写出验证过程；
针对上述各式反映的规律，写出用为自然数，且表示的等式，并验证．23.  本小题分
如图是我国数学家赵爽在周髀算经中给出的图案，人们称它为“赵爽弦图”图中四个全等的直角三角形可以围成一个大正方形，直角三角形两直角边长分别为，，斜边长为，中间的部分是一个小正方形若大正方形的面积是，小正方形的面积是，求的值．
24.  本小题分
如图，中，，于点，于点，且，与交于点，连接．
求证：≌；
求证：；
若，求的长．

答案和解析 1.【答案】 【解析】解：无理数的定义为：无限不循环的小数．
无理数有：，，，共个，
故选：．
根据无理数的定义，即可．
本题考查无理数的定义，解题的关键是掌握无理数的定义．2.【答案】 【解析】解：与不是同类二次根式，不能合并，故A错误，不符合题意；
，故B正确，符合题意；
，故C错误，不符合题意；
，故D错误，不符合题意；
故选：．
根据合并同类二次根式的法则，二次根式的乘除法则逐项判断．
本题考查二次根式的混合运算，解题的关键是掌握二次根式相关的运算法则．3.【答案】 【解析】解：，
，，
，，
．
故选：．
根据非负数的性质计算出、值，再代入所求式计算即可．
本题考查了非负数的性质，两个非负数的和为零，那么这两个非负数都为零．4.【答案】 【解析】解：，
，
，
的值在和之间．
故选：．
先估算出的大小，进而估算的范围．
本题考查了估算无理数的大小，估算无理数大小要用逼近法．5.【答案】 【解析】解：正方形的面积为，正方形的面积为，
，，


正方形的面积是，
故选：．
求出、，再用勾股定理即可得出答案．
本题主要考查正方形的性质、勾股定理、掌握正方形的性质、勾股定理是解题的关键．6.【答案】 【解析】解：如图；．
在中，米，米，
由勾股定理，得：米，
米，即大树折断之前有米高．
故选：．
在折断的大树与地面构成的直角三角形中，由勾股定理易求得斜边的长，进而可求出大树折断之前的高度．
此题考查了勾股定理的应用，属于基础题，解答本题的关键是在直角三角形中运用勾股定理求出的长．7.【答案】 【解析】解：，
，
，
故选：．
根据勾股定理求出的长度，根据弧的半径相等得到的长度，从而求出．
本题考查了实数与数轴，勾股定理，根据勾股定理求出的长度是解题的关键．8.【答案】 【解析】解：，
，
，
数轴上表示的点应在线段上，
故选：．
先估算出的值的范围，然后再估算出的值的范围，即可解答．
本题考查了估算无理数的大小，实数与数轴，熟练掌握估算无理数的大小是解题的关键．9.【答案】 【解析】解：由折叠可知：所在的直线是的垂直平分线，≌，
，
设，则，
，且，
在中，根据勾股定理：，
，
解得，即的长为，
故选：．
由折叠可知：所在的直线是的垂直平分线，≌，，设，用含的式子表示的长，在中，根据勾股定理即可求解．
本题主要考查三角形与折叠问题，掌握折叠的性质，勾股定理的运用是解题的关键．10.【答案】 【解析】解：，
，
的整数部分为，小数部分为，
，
故选：．
根据无理数估算，得到的整数部分为，小数部分为，代值求解即可得到答案．
本题考查无理数估算及代数式求值，二次根式的混合运算，熟练掌握无理数估算是解决问题的关键．11.【答案】 【解析】解：根据题意得：或，
解得：或，
当时，
，
；
当时，
，
；
故选：．
与相等或者互为相反数，分别求出的值，再求出的值，最后求出的值．
本题考查了平方根的定义，体现了分类讨论的数学思想，解题时不要漏解．12.【答案】 【解析】解：如图所示，

三级台阶平面展开图为长方形，宽为，长为，
蚂蚁沿台阶面爬行到点最短路程是此长方形的对角线长，
由勾股定理得，
则蚂蚁沿着台阶面爬到点最短路程是．
故选：．
先将图形平面展开，再用勾股定理根据两点之间线段最短进行解答．
本题主要考查了平面展开图中的最短路径问题，熟练掌握平面展开图及勾股定理是解决本题的关键．13.【答案】 【解析】解：，，
．
故答案为：．
利用算术平方根的意义和二次根式的性质解答即可得出结论．
本题主要考查了算术平方根，二次根式的性质，熟练掌握上述法则与性质是解题的关键．14.【答案】 【解析】解：，
的面积为：．
故答案为：．
根据题中的公式，代入计算求值．
本题考查了二次根式的应用，掌握二次根式的运算法则是解题的关键．15.【答案】   【解析】解：由正方形的面积边长边长，
面积为的正方形的边长为，面积为的正方形的边长为．
，．
两个长方形的面积的和面积为的正方形面积为的正方形．
故答案为：，，．
依据正方形的面积公式可求及，再用大正方形的面积减去两个小正方形的面积即得两个长方形的面积和．
本题考查了正方形的面积公式的逆运用及二次根式的加减，需要熟练掌握运算技巧解题．16.【答案】 【解析】解：，
，
，
，
．
故答案为：．
要比较与的大小，就是比较与的大小，就要比较与的大小，就要比较与的大小，就比较与的大小即可．
本题主要考查了实数的比较大小，解题的关键是把通分成，分母相同，比较分子的大小．17.【答案】 【解析】解：由题意得，，，
设，则，
在中，，
即：，
解得：．
答：的长为．
故答案为：．
设，则，在中利用勾股定理列出方程，进而解答即可．
此题考查了勾股定理在实际生活中的应用，正确应用勾股定理是解题关键．18.【答案】 【解析】解：在中，，，，
，
，
连接，
由作图知垂直平分，
，
，
，
，
，
；
故答案为：．
根据勾股定理的逆定理得到，连接，由作图知垂直平分，得到，根据勾股定理即可得到结论．
本题主要考查了作图基本作图，垂直平分线的性质，勾股定理，勾股定理的逆定理，解题的关键是正确画出辅助线，构造直角三角形，用勾股定理求解．19.【答案】解：的立方根是，的算术平方根是，
，，
，，
，
，
是的整数部分，
．
将，，代入得：，
的平方根是． 【解析】此题考查立方根的意义、算术平方根的意义、无理数的估算方法、平方根的意义、代数式求值等知识点，读懂题意，掌握解答顺序，正确计算即可．
利用立方根的意义、算术平方根的意义、无理数的估算方法，求出、、的值；
将、、的值代入代数式求出值后，进一步求得平方根即可．20.【答案】解：







 【解析】先根据二次根式的性质化简，再根据二次根式的乘法法则计算，再算加减即可；
先根据乘法公式计算，再算加减即可．
本题考查了二次根式的混合运算，熟练掌握二次根式的运算法则是解答本题的关键，整式的乘法的运算公式及运算法则对二次根式的运算同样适应．21.【答案】解：在中，米，米，
米．
答：梯子的顶端距地面米；
在中，米，
米，
米．
答：梯子的底端在水平方向滑动了米． 【解析】此题主要考查了勾股定理的应用，关键是从题中抽象出勾股定理这一数学模型，画出准确的示意图．领会数形结合的思想的应用．
利用勾股定理可得，再计算即可；
在直角三角形中计算出的长度，再计算即可．22.【答案】解：答案不唯一，如：，，
证明：；
，
证明：． 【解析】按照规律写猜想并证明；
按规律写出第一个数换为，第二个数换为，第三个数换为的等式．
本题考查了算术平方根的计算和等式证明，认真阅读条件式子再根据规律猜想和证明是解题关键．23.【答案】解：大正方形的面积是，小正方形的面积是，
，，
，
即，
，
． 【解析】根据大正方形的面积是，小正方形的面积是，得出，，得出的值，即可得出结果．
本题考查了勾股定理的证明，正确得出是解题的关键．24.【答案】证明：，，
，
，，，
，
在和中，
，
≌；
证明：≌，
，
，，
，
即，
．
解：≌，
，
，
，，
，即且平分，
，
． 【解析】先证明，再根据即可证明≌；
根据全等得出，根据等腰三角形的性质求出，即可得出答案；
证明；求出，即可解决问题．
此题考查了全等三角形的判定，等腰直角三角形的性质，线段垂直平分线的性质，勾股定理等知识；应牢固掌握全等三角形的判定，等腰直角三角形的性质等知识点，并灵活运用．