2023-2024学年陕西省西安交大附中浐灞右岸学校八年级（上）开学数学试卷（含解析）

这是一份2023-2024学年陕西省西安交大附中浐灞右岸学校八年级（上）开学数学试卷（含解析），共14页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2023-2024学年陕西省西安交大附中浐灞右岸学校八年级（上）开学数学试卷一、选择题（本大题共8小题，共24.0分。在每小题列出的选项中，选出符合题目的一项）1.  下列不是轴对称图形是(    )A.  B.  C.  D. 2.  下列各数：，，，，两个之间依次多一个，中无理数的个数为(    )A. 个 B. 个 C. 个 D. 个3.  的值等于(    )A.  B.  C.  D. 4.  下列条件中，不能判定为直角三角形的是(    )A. ：：：：
B. ，，
C. ：：：：
D. ：：：：5.  如图，，将直角三角板其中按图示放置，点在上，点在上，若平分，则的度数为(    )
 A.  B.  C.  D. 6.  如图，在中，，，，沿过点的直线折叠，使点落在边上的点处，再次折叠，使点与点重合，折痕交于点，则的长度为(    )
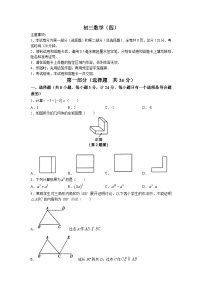
 A.  B.  C.  D. 7.  若用、、三幅图分别表示变量之间的关系，将下面的、、对应的图象排序(    )

竖直放置的弹簧在弹性限度内，弹簧的长度和所挂物体质量的关系；
面积为定值的矩形中，矩形的相邻两边长之间的关系；
运动员推铅球时，铅球的高度与水平距离的关系．A.  B.  C.  D. 8.  如图，在中，，以的三边为边向外作正方形，正方形，正方形，连结，，作交于点，记正方形和正方形的面积分别为，，若，，则：等于(    )A. ：
B. ：
C. ：
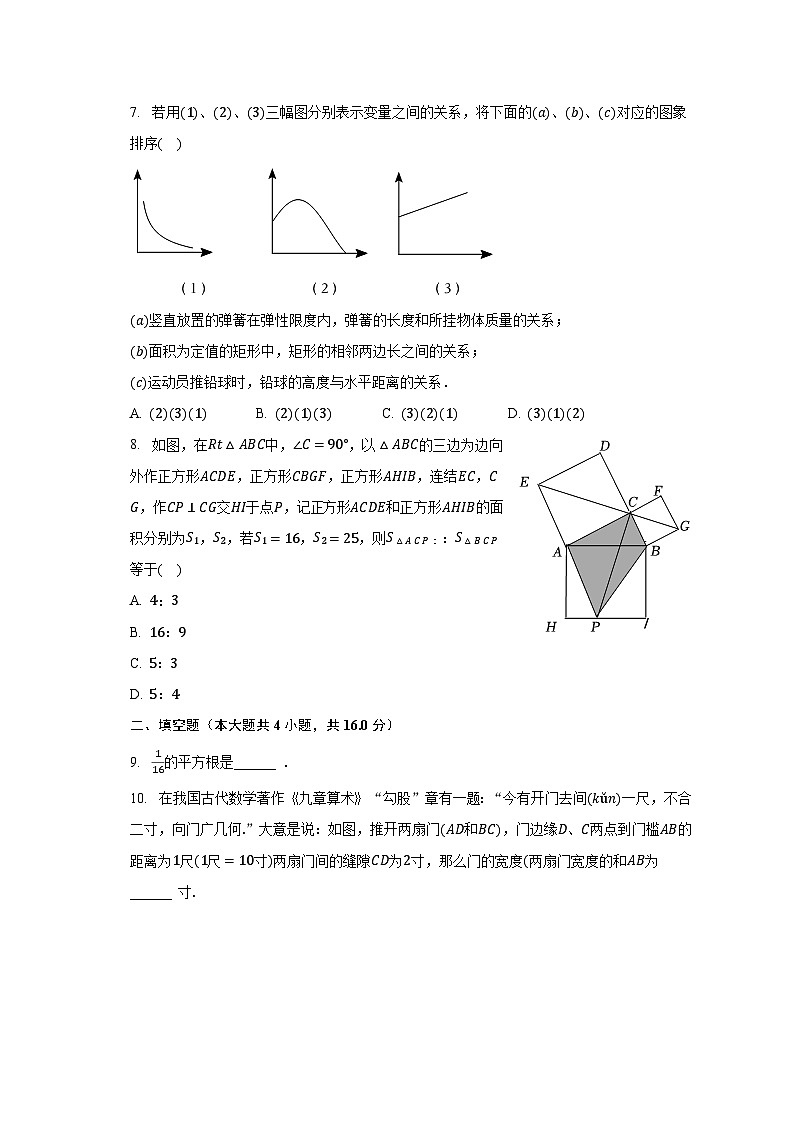
D. ：二、填空题（本大题共4小题，共16.0分）9.  的平方根是______ ．10.  在我国古代数学著作九章算术“勾股”章有一题：“今有开门去间一尺，不合二寸，向门广几何”大意是说：如图，推开两扇门和，门边缘、两点到门槛的距离为尺尺寸两扇门间的缝隙为寸，那么门的宽度两扇门宽度的和为______ 寸
11.  如图，圆柱形玻璃杯高为，底面周长为，在杯内壁底的点处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿与蜂蜜相对的点处，则蚂蚁从外壁处到内壁处的最短距离是杯壁厚度不计 ______ ．
 12.  已知和均为等腰直角三角形，，，点为的中点，已知为直线上的一个动点，连接，则的最小值为______ ．
 三、解答题（本大题共6小题，共60.0分。解答应写出文字说明，证明过程或演算步骤）13.  本小题分
计算：
；
．14.  本小题分
已知，，
化简；
若，求的值．15.  本小题分
在一个不透明的口袋中放入个白球和个红球，它们除颜色外完全相同．
求从口袋中随机摸出一个球是白球的概率；
现从口袋中取出若干个红球，并放入相同数量的白球，充分摇匀后，要使从口袋中随机摸出一个球是白球的概率是，问取出了多少个红球？16.  本小题分
如图，在中，是边上的高，是边上的高，且，交于点，若，，，求线段的长度．
17.  本小题分
图是某品牌婴儿车，图为其简化结构示意图．根据安全标准需满足，现测得，，，其中与之间由一个固定为的零件连接即，通过计算说明该车是否符合安全标准．

 18.  本小题分
探究：如图所示，为线段上一动点，分别过点，点作，，分别连接，已知，，设．
______，______用含的代数式表示；
探究点，，处于何种位置时，的值最小，并求出其最小值；
根据中的探究结果，请构图并求出代数式的最小值．要求画出示意图

答案和解析 1.【答案】 【解析】解：选项B、、能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以是轴对称图形，
选项A不能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以不是轴对称图形，
故选：．
根据如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行分析即可．
本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．2.【答案】 【解析】解：，
故无理数有，，两个之间依次多一个，共个．
故选：．
根据无理数的定义判断即可．
本题考查了无理数的识别，无限不循环小数叫无理数，初中范围内常见的无理数有：类，如；开方开不尽的数，如；具有特殊结构的数，如两个之间依次增加个，两个之间依次增加个．3.【答案】 【解析】解：原式，
故选：．
根据算术平方根的概念计算．
本题主要考查了算术平方根的概念，用概念计算是解题关键．4.【答案】 【解析】解：、因为：：：：，设，，，所以，故是直角三角形；
B、因为，故是直角三角形；
C、：：：：，且，所以，故是直角三角形；
D、：：：：，且，所以，故不是直角三角形．
故选：．
利用直角三角形的定义和勾股定理的逆定理逐项判断即可．
本题考查了勾股定理的逆定理：如果三角形的三边长，，满足，那么这个三角形就是直角三角形．也考查了三角形内角和定理．掌握勾股定理的逆定理的内容是解题的关键．5.【答案】 【解析】解：平分，，
，，
，
，
，
故选：．
根据角平分线的定义得出，进而利用两直线平行，同旁内角互补解答即可．
此题考查平行线的性质，关键是利用两直线平行，同旁内角互补解答．6.【答案】 【解析】解：，，，
，
由折叠得，，，，
，
，
，，
，
，
故选：．
由折叠得，，，，则，所以，由勾股定理得，求得，于是得到问题的答案．
此题重点考查直角三角形的两个锐角互余、轴对称的性质、勾股定理等知识，证明是解题的关键．7.【答案】 【解析】解：竖直放置的弹簧在弹性限度内，弹簧的长度和所挂物体质量的关系是一次函数关系，图象是直线，故符合；
面积为定值的矩形中，矩形的相邻两边长之间的关系是反比例函数关系，图象是双曲线，符合；
运动员推铅球时，铅球的高度与水平距离的关系是二次函数关系，图象是抛物线，符合．
故选：．
根据题意分析得出函数关系，结合图象即可求解．
本题考查了一次函数、反比例函数、二次函数的应用，根据题意得出函数关系是解题的关键．8.【答案】 【解析】解：如图所示，过点作，交的延长线于点，作，交的延长线于点，

由题可得，，，
，
又，
，即平分，
又，，
，
正方形和正方形的面积分别为，，且，，
正方形的面积，
正方形和正方形的面积之比为：，
：：，
，
即：等于：．
故选：．
过点作，交的延长线于点，作，交的延长线于点根据平分，即可得出再根据正方形和正方形的面积之比为：，即可得到：：，进而利用三角形面积公式得到：的值．
本题主要考查了勾股定理以及角平分线的性质的运用，解决问题的难点是利用角平分线的性质发现，将：的值转化为：的值．9.【答案】 【解析】解：的平方根是，
故答案为：．
根据平方根的定义即可求出答案．
本题考查平方根的定义，解题的关键是正确理解平方根的定义，本题属于基础题型．10.【答案】 【解析】解：设，过作于，
则，，．
在中，
，即，
解得．
故门的宽度两扇门的和为寸．
故答案为：．
画出直角三角形，根据勾股定理即可得到结论．
本题考查了勾股定理的应用，熟练掌握勾股定理是解题的关键．11.【答案】 【解析】解：如图，将杯子侧面展开，作关于的对称点，
连接，则即为最短距离，
在直角中，由勾股定理得，
．
则蚂蚁从外壁处到内壁处的最短距离为，
故答案为：．
将杯子侧面展开，建立关于的对称点，根据两点之间线段最短可知的长度即为所求．
本题考查了平面展开最短路径问题，将图形展开，利用轴对称的性质和勾股定理进行计算是解题的关键．12.【答案】 【解析】解：设是的中点，连接，

，
，
即，
，为中点，
，
在和中，
，
≌，
，
点在直线上运动，
当时，最小，
是等腰直角三角形，
，
，
是等腰直角三角形，
，
，
，
线段的最小值是为
故答案为．
设是的中点，连接，先证得≌，得出，根据点到直线的距离可知当时，最小，然后根据等腰直角三角形的性质求得时的的值，即可求得线段的最小值．
本题考查了等腰直角三角形的性质、三角形全等的判定和性质、垂线段最短等知识，解题的关键是学会添加辅助线构建全等三角形，学会利用垂线段最短解决最值问题，属于中考常考题型．13.【答案】解：

；

． 【解析】根据实数的运算法则计算即可；
根据整式的混合运算法则计算即可．
本题考查了实数的运算，整式的混合运算，熟练掌握这些运算法则是解题的关键．14.【答案】解：，，



；
，
，，
，，



． 【解析】把和的值代入式子中进行计算，即可解答；
根据绝对值和偶次方的非负性可得，，从而可得，，然后把，的值代入的结论进行计算，即可解答．
本题考查了整式的混合运算化简求值，完全平方公式，平方差公式，绝对值和偶次方的非负性，准确熟练地进行计算是解题的关键．15.【答案】解：口袋中共有个白球和个红球，
一共有球个，
摸出白球．
答：从口袋中随机摸出一个球是白球的概率是；
设取出了个红球．
根据题意，得，
解这个方程，得．
答：取出了个红球． 【解析】用白球的个数除以球的总个数即可；
设取走了个红球，根据概率公式列出算式，求出的值即可得出答案．
本题考查了概率的知识．用到的知识点为：概率所求情况数与总情况数之比．16.【答案】解：是边上的高，是边上的高，
，
，
，
在和中，
，
≌，
，，
． 【解析】利用证明≌，得，，即可得出答案．
本题主要考查了全等三角形的判定与性质，证明≌是解题的关键．17.【答案】解：在中，，
在中，，
，
，
．
故该车符合安全标准． 【解析】在中，由勾股定理求出，在中，通过计算，根据勾股定理逆定理判断即可．
本题主要考查了勾股定理和勾股定理逆定理，熟练掌握勾股定理逆定理的应用是解决问题的关键．18.【答案】  【解析】解：，；
故答案为：，；

当点、、三点在一条直线上时，的值最小，过点作交的延长线于点则四边形是矩形，

，，
，
，
的最小值为．

如图，令，，，设，则．

，
、、三点在一条直线上时，的值最小，
的长即为的最小值，
过点作的平行线交的延长线于点，
于，于，
，
四边形是矩形，
，，
在中，，，，
，
的最小值为．
由两点之间线段最短可知：当点、、三点在一条直线上时，的值最小；
根据勾股定理计算即可；
如图，令，，，设，则过点作的平行线交的延长线于点，再证明四边形是矩形，根据矩形的性质和勾股定理即可出代数式的最小值．
本题考查了最短路线问题，综合利用了勾股定理，及用数形结合的方法求代数式的值的方法，利用两点之间线段最短是解决问题的关键．