宁夏银川市第六中学2023届九年级上学期第一次月考数学试卷(含解析)

;

2022-2023学年宁夏银川六中九年级（上）

第一次月考数学试卷

一、选择题（本大题共10小题，共30.0分．在每小题列出的选项中，选出符合题目的一项）

1．用配方法解方程x2+4x-1=0，下列配方结果正确的是（　　）

A． B． C． D．

2．顺次连接矩形四边中点所得的四边形一定是（    ）

A．正方形 B．矩形 C．菱形 D．等腰梯形

3．把方程化成一般式，则二次项系数，一次项系数，常数项的值分别是（  ）

A．，， B．，， C．，， D．，，

4．下列命题是真命题的是（    ）

A．一组邻边相等的平行四边形是菱形

B．菱形的对角线相等

C．对角线互相垂直的平行四边形是正方形

D．四边都相等的四边形是矩形

5．在一次酒会上，每两人都只碰一次杯，如果一共碰杯55次，则参加酒会的人数为（ ）

A．9人 B．10人 C．11人 D．12人

6．如图，已知四边形是平行四边形，下列结论中不正确的是（　　）

A．当时，它是菱形 B．当时，它是菱形

C．当时，它是矩形 D．当时，它是正方形

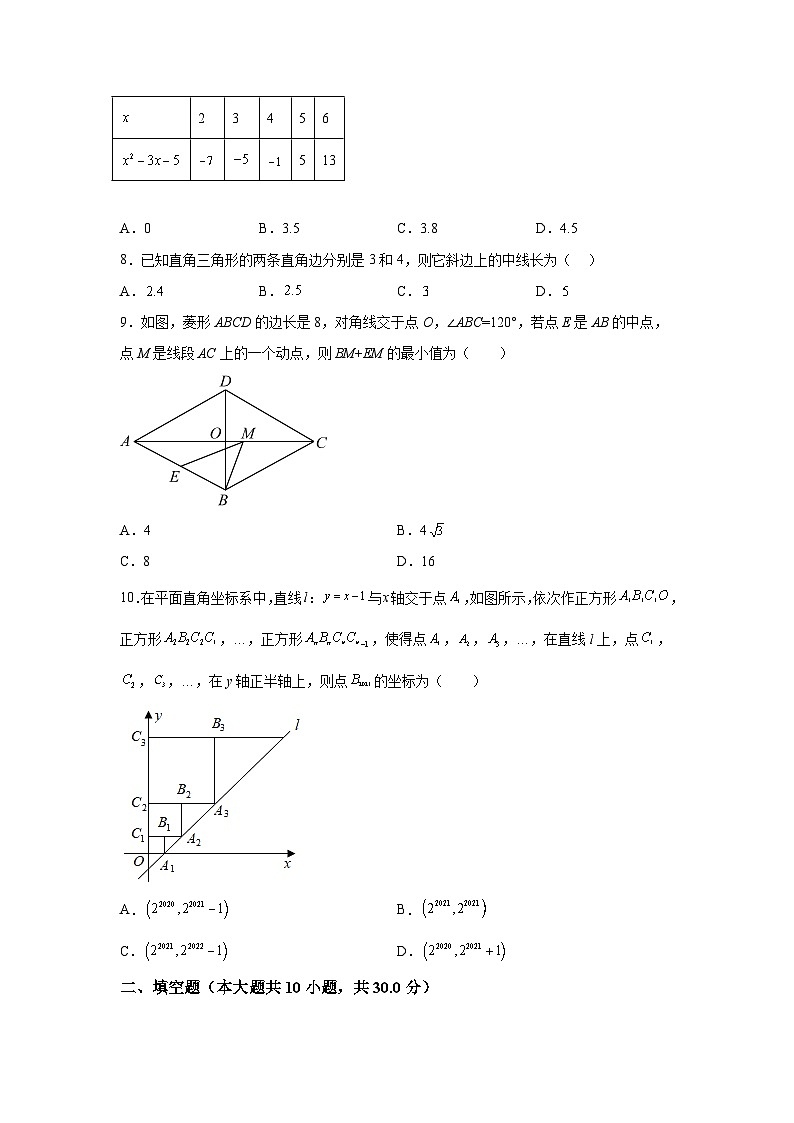
7．根据下表提供的信息，一元二次方程的解大概是（    ）

A．0 B．3.5 C．3.8 D．4.5

8．已知直角三角形的两条直角边分别是3和4，则它斜边上的中线长为（    ）

A． B． C． D．

9．如图，菱形ABCD的边长是8，对角线交于点O，∠ABC=120°，若点E是AB的中点，点M是线段AC上的一个动点，则BM+EM的最小值为（　　）

A．4 B．4

C．8 D．16

10．在平面直角坐标系中，直线l：与x轴交于点，如图所示，依次作正方形，正方形，…，正方形，使得点，，，…，在直线l上，点，，，…，在y轴正半轴上，则点的坐标为（　　）

A． B．

C． D．

二、填空题（本大题共10小题，共30.0分）

11．关于的一元二次方程的解是________．

12．方程是关于x的一元二次方程，则_________．

13．如图，矩形ABCD的两条对角线相交于点O，已知∠AOD=120°，AB=2cm，则矩形对角线BD的长为________cm．

14．如图，菱形的对角线，，交的延长线于，则的长为______．

15．把化成的形式，则______．

16．如图，在矩形纸片ABCD中，AB=12，BC=5，点E在AB上，将DAE沿DE折叠，使点A落在对角线BD上的点处，则AE的长为___．

17．如图所示，在中，，，，点从点开始沿边向点以的速度运动，同时，另一点从点开始以的速度沿边向点运动______秒钟后，的面积是面积的．

18．如图所示，在中，以为圆心，长为半径画弧交于点，再分别以点、为圆心，大于为半径画弧，两弧交于一点，连结交于点，连结．若，，则四边形的面积为____．

19．若是方程的一个根，则式子的值为__________．

20．将矩形纸片ABCD按如图所示的方式折叠，恰好得到菱形AECF．若AB＝3，则菱形AECF的面积为_____．

三、计算题（本大题共1小题，共12.0分）

21．阅读理解并解答：

【方法呈现】

(1)我们把多项式及叫做完全平方式．在运用完全平方公式进行因式分解时，关键是判断这个多项式是不是一个完全平方式，同样地，把一个多项式进行局部因式分解可以来解决代数式值的最小或最大问题．

例如：，

，

．

则这个代数式的最小值是______，这时相应的的值是______．

【尝试应用】

(2)求代数式的最小或最大值，并写出相应的的值．

(3)已知，，是的三边长，满足，且是中最长的边，求的取值范围．

四、解答题（本大题共4小题，共48.0分．解答应写出文字说明，证明过程或演算步骤）

22．解下列方程．

(1)；

(2)；

(3)；

(4)．

23．游行队伍有8行12列，后又增加了69人，使得队伍增加的行、列数相同，你知道增加了多少行或多少列吗？

24．如图，已知菱形中，对角线、相交于点，过点作，过点作，与相交于点．

(1)求证：四边形是矩形；

(2)若，，则四边形的周长为 　 　．

25．如图，在一块宽为，长为的长方形草地上，修建同样宽的小路后，剩下的草坪面积为，求修建的小路的宽度．

答案

1．A

解析：解：把方程x2+4x﹣1=0的常数项移到等号的右边，

得到x2+4x=1

方程两边同时加上一次项系数一半的平方，

得到x2+4x+4=1+4

配方得（x+2）2=5．

故选：A．

2．C

解析：解：如图，连接AC、BD

在△ABD中，∵AH=HD，AE=EB

∴EH=BD

同理FG=BD，HG=AC，EF=AC

又∵在矩形ABCD中，AC=BD

∴EH=HG=GF=FE

∴四边形EFGH为菱形

故选C．

3．A

解析：解：由方程，得

，

、、的值分别是、、；

故选A．

4．A

解析：A. 一组邻边相等的平行四边形是菱形，故该选项正确，符合题意；

B. 菱形的对角线互相垂直平分，故该选项不正确，不符合题意；

C. 对角线互相垂直且相等的平行四边形是正方形，故该选项不正确，不符合题意；

D. 四边都相等的四边形是菱形，故该选项不正确，不符合题意；

故选A．

5．C

解析：设参加酒会的人数为x人，依题可得：

x（x-1）=55，

化简得：x2-x-110=0，

解得：x1=11，x2=-10（舍去），

故答案为C.

6．D

解析：解：A、∵四边形是平行四边形，，

∴四边形是菱形，说法正确，不符合题意；

B、∵四边形是平行四边形，，

∴四边形是菱形，说法正确，不符合题意；

C、∵四边形是平行四边形，，

∴四边形是矩形，说法正确，不符合题意；

D、∵四边形是平行四边形，，

∴四边形是矩形，说法错误，符合题意；

故选D．

7．D

解析：时，，

时，，

则的解的范围为，

即一元二次方程的解大概是4.5．

故选D．

8．B

解析：解：由勾股定理得，斜边=，

所以，斜边上中线长=，

故选：B．

9．B

解析：解：连接DE交AC于M，

由菱形的对角线互相垂直平分，可得B、D关于AC对称，则MD = MB，

ME十MB=ME+MD≥DE，即DE就是ME十MB的最小值，

∵∠ABC=120°，∠BAD = 60°，AD＝ AB＝8，△ABD是等边三角形，

∵点E是AB的中点，

∴AE= BE＝4，DE⊥AB(等腰三角形三线合一的性质)，

在Rt△ADE中，由勾股定理可得： ，

故选：B．

10．A

解析：解：当时，有，

解得：，

∴点的坐标为．

∵四边形为正方形，

∴点的坐标为．

同理，可得出：，，，，…，

∴，，，，…，

∴（n为正整数），

∴点的坐标为．

故选：A

11．

解析：解：，

∴，

∴，

∴，

故答案为：．

12．-3

解析：解：∵方程是关于x的一元二次方程

所以|n|-1=2，n-3≠0

解得n=-3

故答案为：-3.

13．4

解析：解：∵四边形ABCD是矩形，

∴AC＝BD，OA＝OC＝AC，BO＝DO＝BD，∠BAD＝90°，

∴OA＝OB，

∵∠AOD＝120°，

∴∠AOB＝60°，

∴△AOB是等边三角形，

∴∠ABO＝60°，∠ADB＝30°，

∴BD＝2AB＝4（cm）．

故答案为：4．

14．##

解析：解：与相交于点，

四边形是菱形，，

，，，

，

菱形的面积，

即，

解得：，

故答案为：．

15．3

解析：解：，

方程移项得：，

配方得：，

即，

可得，

故答案为：．

16．

解析：∵AB=12，BC=5，

∴AD=5，

∴，

根据折叠可得：AD=A′D=5，

∴A′B=13－5=8，

设AE=x，则A′E=x，BE=12－x，

在Rt△A′EB中：，

解得：．

故答案为：

17．5

解析：∵

∴

∵

∴

∴．

设秒后的面积是面积的

∴

依题意得

∴

∴或（舍去）

∴秒后的面积是面积的．

故答案为：5

18．24

解析：解：连接、．

由图可得，

在和中，

∵四边形ABCD是平行四边形，

∴AD∥BC，

∴∠DAE=∠AEB，

∴∠BAE=∠AEB，

∴AB=BE，

又∵AF∥BE，

∴四边形ABEF是平行四边形，

∵AB=BE，

∴平行四边形ABEF是菱形，

∴AE与BF互相垂直平分，

∴∠AOB=90°，，

∵AB=5，

在中，

．

故答案为：24

19．2020

解析：由题意知，，即，

∴，

故答案为：2020．

20．

结合直角三角形勾股定理求得BC的长，则利用菱形的面积公式即可求解．

解析：解：∵四边形AECF是菱形，AB＝3，

∴设BE＝x，则AE＝3﹣x，CE＝3﹣x，

∵四边形AECF是菱形，

∴∠FCO＝∠ECO，

∵∠ECO＝∠ECB，

∴∠ECO＝∠ECB＝∠FCO＝30°，

∴2BE＝CE，

∴CE＝2x，

∴2x＝3﹣x，

解得：x＝1，

∴CE＝2，利用勾股定理得出：

BC2+BE2＝EC2，

BC＝

又∵AE＝AB﹣BE＝3﹣1＝2，

则菱形的面积＝AE•BC＝．

故答案为．

21．(1)2，；

(2)有最大值，相应的的值为；

(3)．

解析：（1）解：∵代数式

∴代数式的最小值是，这时相应的的值是，

故答案为：，；

（2）解：

，

∵

∴，

∴代数式有最大值，相应的的值为；

（3）解：∵a，，是的三边长，满足，

∴，

∴，

∴，

∴，，

∴，，

∵，

∴，

是中最长的边，

∴．

答：的取值范围为．

22．(1)，；

(2)，；

(3)，；

(4)，．

解析：（1）解：，

，

，

所以，；

（2）解：，

，

或，

所以，；

（3）解：，

，

，

，

，

所以，；

（4）解：．

，

或，

所以，．

23．增加了3行3列

解析：解：设增加了x行x列，

根据题意得：，

整理得：，

解得：（不合题意，舍去）．

答：增加了3行3列．

24．(1)见解析

(2)14

解析：（1）证明：，，

四边形为平行四边形，

四边形为菱形，

，

，

平行四边形是矩形；

（2）解：四边形为菱形，

，，，

在中，由勾股定理得，

，

，

四边形的周长．

故答案为：14．

25．

解析：解：设修建的小路的宽度为xm，

则，

化简得，

解得（舍去）．

答：修建的小路的宽度为．